标签：链表实现   迭代   相等   search   解决   eal   错题   代码调试   数据结构   

20172305 2018-2019-1 《Java软件结构与数据结构》第七周学习总结

教材学习内容总结

本周内容主要为书第十一章内容：

• 二叉查找树(附加属性的二叉树)
  • 二叉查找树是对树中的每个结点，其左结点都要小于其父结点，而父结点又小于或等于其右结点。
  • 二叉查找树的定义是二叉树定义的扩展。
• LinkedBinarySearchTree类的相关方法：

  • addElement操作(类似有序列表的添加方法，元素必须是Comparable，不是的话会抛出NoComparableElementException异常)

    • 如果树为空，则新元素成为根结点
    • 如果树非空，则新元素会与树根,元素进行比较。
    • 

  • removeElement操作(类似列表的删除指定元素的方法,找不到给定目标元素则抛出ElementNotFoundException异常)

    • 在树中找不到给定目标元素时，会抛出ElementNotFoundException异常。
    • 在树中找到给定目标元素时，如果被删除结点没有子结点，则替代元素为null；如果被删除结点只有一个结点，则替代元素为该结点；如果被删除结点有两个子结点，则替代元素用中序查找。
    • 

  • removeAllOccurrences操作(删除指定元素的所有存在，如果找不到给定目标元素则抛出ElementNotFoundException异常，如果找到元素不是Comparable，则抛出ClassCastException异常)

    • 调用LinkedBinaryTree类的contains方法确定树中是否含有目标元素。
    • 调用removeElement来实现删除元素，并确保当树中没有该元素的时候抛出异常。(然后捕获异常不输出任何内容)

  • removeMin操作(查找最小元素 + 删除目标元素)

    • 如果树根没有左子结点，则树根就是最小元素，而树根的右子结点将成为新的根结点。
    • 如果树的最左侧结点是叶结点，则叶结点就是最小元素，这是只需定义父节点的左子结点为null。
    • 如果树的最左侧结点是一个内部节点，则需要设置其父节点的左结点引用指向这个将删除结点的右结点。

• 蜕化树(类似链表，但比链表的效率低，每一个结点要附带额外的开销)

  

• 平衡二叉查找树，自树根而下的路径最大长度必须不超过log2n，而且字树根而下的路径最小长度必须不小于log2n-1。
  • 右旋(左结点绕着其父结点向右旋转):根结点的左子结点成为新的树根，原根结点元素成为根节点的右子结点元素，原树根的左子结点的右子结点成为原树根的新的左子结点。
    
  • 左旋(右结点绕着其父结点向左旋转)：根结点的右子结点成为新的树根，原根结点元素成为根节点的左子结点元素，原树根的右子结点的左子结点成为原树根的新的右子结点。
    
  • 右左旋(先让树根右结点的左子结点，绕着树根的右结点进行一次右旋，然后再让所得树根右结点绕着树根进行一次左旋)
  • 左右旋(先让树根左结点的右子结点，绕着树根的左结点进行一次左旋，然后再让所得树根左结点绕着树根进行一次右旋)
• 平衡二叉查找树--AVL树使用每个结点的平衡因子来保持二叉查找树平衡的策略。
  • 平衡因子：某结点的右子树的高度减去左子树的高度。
  • 平衡因子大于1或是小于-1则需要以该结点为树根的子树进行重新平衡。

• 平衡二叉查找树--红黑树(非严格意义上的平衡二叉树)使用与每个结点相关颜色(红色或是黑色)来保持二叉查找树平衡的策略。

  • 红黑树满足的性质：
  • (1.)每个结点或是红色或是黑色
  • (2.)根结点是黑色的
  • (3.)每个叶结点(为空)都是黑色的
  • (4.)如果一个结点是红色，则他的两个子结点都是黑色
  • (5.)对每个结点，从该结点到子孙结点的所有路径上包含相同数目的黑结点

教材学习中的问题和解决过程

• 问题1:红黑树的添加删除方法?
• 问题1解决方案：
  • 添加元素的判断条件：

  • 添加元素的父节点是添加元素的祖父节点的左结点：

    • 情况一添加结点的叔叔是红色的，针对这种情况，我们将双亲结点和叔叔结点为黑色，然后将祖父结点染成红色，再以祖父结点设为当前结点实现递归向上，直至到根结点为止。
    • 情况二添加结点的叔叔是黑色的，添加结点是右结点。这种情况需要先旋转到第三种情况，即以添加结点的父结点为支点进行左旋达到第三种情况，再按照第三种情况进行。
    • 情况而添加结点的叔叔是黑色的，添加结点是左结点。这种情况需要将双亲结点染为黑色，祖父结点染为红色，以祖父结点为支点进行左旋。

  • 添加结点的父结点是添加元素的祖父结点的右结点：

    • 第一种情况 是添加结点的叔叔是红色的，这种情况和上一种大前提下的情况一致，将双亲结点和叔叔结点染为黑色，然后再将祖父结点染为红色，将祖父结点视为新的结点实现递归，直至传到根节点。
    • 第二种情况 是添加结点的叔叔是黑色的，而且添加结点是左子结点，这种情况需要先旋转到第三种情况，即以添加结点的父结点为支点进行右旋达到第三种情况，再按照第三种情况进行。
    • 第三种情况 是添加结点的叔叔是黑色的，而且添加结点是右子结点。这种情况需要将双亲结点染为黑色，祖父结点染为红色，以祖父结点为支点进行左旋。

  • 删除操作(删除操作理解浅谈)

    • 第一种情况 删除结点的兄弟是红色的，删除结点的兄弟是红色的，那么父亲结点是黑色的，这种情况就需要改变两个结点的颜色，然后以父结点为支点进行左旋，达到第二种情况或是第三种情况或是第四种情况
    • 第二种情况 删除结点的兄弟是黑色的，而且兄弟结点的两个结点都是黑色的
    • 第三种情况 删除结点的兄弟是黑色的，而且兄弟结点的左子结点为红色，右子结点为黑色，针对这种情况，我们先将兄弟结点和左子结点的颜色交换，即变色后以兄弟结点为支点进行右旋达到第四种情况
    • 第四种情况 删除结点的兄弟结点是黑色的，而且兄弟结点的右结点是红色

代码学习中的问题和解决过程

• 问题1：PP11.10的add操作如何实现递归?

• 问题1的解决方案：遇到这道题目，第一感觉就是很迷，不知从何下手，而且说的add操作在二叉查找树的链表实现中也叫addElement操作。而且addElement的操作用到了递归，一个方法调用另一个递归的方法，所以我在此基础上进行了两个方法的结合，常使用一个递归的方法来实现。其实addElement操作，之所以分成两个方法的原因是调用递归的方法进行着根结点是否为空，空的话就实现根结点等于添加元素；以及判断元素是否是Comparable类型，而递归的方法是要进行添加元素到某一个结点的左侧或是右侧。从两者的实现差异来看，递归的方法需要两个参数实现，而调用递归的方法只需要一个参数，把参数的内容插入到树上就行。但是如果把两者结合把调用递归的方法也改成两个参数的，尝试了一下结果是出现这种排不了序的结果。只是在上一步产生的树的整体进行一个比较，而不是针对每一个结点的元素比较。

  • 错误示例：
    

• 问题2：在无返回值的条件下语句有return的作用？

• 问题2的解决方案：return的使用一直在存在返回值条件下使用，但是从未在无返回值条件下使用。如果return后面不接内容的话，就会结束该方法并不会输出任何内容的。

  • 

    • (1.)return语句：是指结束该方法，继续执行方法后的语句。
    • (2.)break语句：是指在循环中直接退出循环语句（for，while，do-while，foreach），break之后的循环体里面的语句也执行。
    • (3.)continue语句：是指在循环中中断该次循环语句（for，while，do-while，foreach），本次循环体中的continue之后语句不执行，直接跳到下次循环。

• 问题3：removeMax、findMax、findMin如何编写？

  • removeMax：删除树中的最大元素
  • findMax:返回树中最小元素的引用
  • findMin：返回树中最大元素的引用

• 问题3解决方案：书中给出了删除最小元素的方法，根据提供的代码以及二叉查找树的了内部结构，最小元素在根结点的左侧查找，那么最大元素则在根结点的右侧查找。具体分析一下删除最小元素，根据二叉查找树的结构可以发现在查找最小元素的时候，如果根结点的左侧没有子结点，那么根结点即为要删除的最小结点，根结点的右侧子节点为新的根结点。如果根结点的左侧有子结点，那么遍历左侧找到最小的结点，但是直接删除给节点是不行的，要考虑到删除的该结点的时候有可能存在其右子结点，这是要把右子结点移到删除结点的位置。所以，删除最大元素，也分两种情况，在根结点的右侧没有子结点，那么根结点即为要删除的最大元素，根结点的左侧元素即为根结点。如果根结点的右侧右子结点，那么遍历右侧找到最大的结点，把该结点的左子结点替代到删除的位置。而查找的方法只需在省略删除结点的子结点替代删除位置的相关代码就行。

• 问题4：AVL树的左旋、右旋、左右旋、右左旋的方法实现?

• 问题4解决方案：AVL树的旋转是利用各结点的平衡因子来确定是否平衡，如果不平衡根据各结点的平衡因子的大小进行计算。

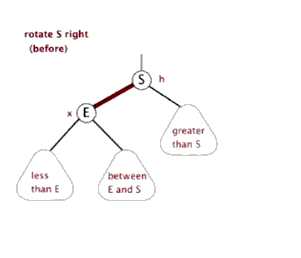
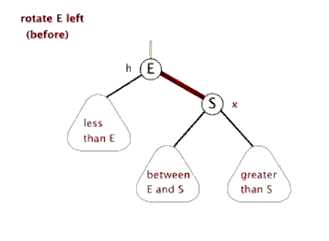
  • 左旋：根结点右子结点成为新的根结点，右子结点的左子结点成为原根节点的右子结点。
    
  • 右旋：根结点左子结点成为新的根结点，左子结点的右子结点成为原根结点的左子结点。
    
  • 左右旋：以根结点的左子结点为新的根结点，进行左旋(根结点的新左子结点为原左子结点的右子结点)，然后在以原根结点进行右旋。
    
  • 右左旋：以根结点的右子结点为新的根结点，进行右旋(根结点的新右子结点为原右子结点的左子结点)，然后在以原根结点进行左旋。
    

• 问题5：AVL树的添加和删除方法如何编写？
• 问题5解决方案：

  • addElement操作：在插入元素的之前，先判断元素是否是Comaprable类型以及判断插入的结点是否为空，如果为空的话就构造一个新的AVL树(左右子结点均为null)，然后开始个插入结点位置进行判断。

    • 如果比目标结点小的话，进行结点的左侧插入，通过以目标结点的左子结点为新的根结点进行判断实现递归操作。因为我们已经确定是在左侧添加元素，那么整棵树的左侧高度必然要大于右侧高度，但是我们不确定差值是多少，但是差值也只能为-2或-1或0(右侧高度减左侧高度)。所以根据差值进行判断，如果相差为-2，那么添加元素后需要进行平衡。通过判断新加元素在左侧树的左侧还是右侧，如果在左侧直接进行一次右旋；在右侧进行一次左右旋。
    • 如果比目标结点大或是相等的话，进行结点的右侧插入，通过以目标结点的右子结点为新的根结点进行判断实现递归操作。在确定在右侧添加之后，右侧高度会比左侧高度要大，但是差值也只能为2或1或0(右侧高度减左侧高度)。所以根据差值进行判断，如果相差为2，那么添加元素后需要进行平衡。通过判断新加元素在右侧树的左侧还是右侧，如果在左侧直接进行一次右左旋；在右侧进行一次左旋。

  • removeElement操作：在删除元素之前，先判断结点是否为空，在不为空的前提下进行删除操作。

    • 如果删除元素在根结点的左侧，通过以根结点的左子结点为新的根结点进行判断实现递归操作。因为在删除元素之前，整棵树都是平衡的，所以每个结点的平衡因子都是0或1或-1，而在删除元素之后，导致整棵树不平衡，但是也只会出现不平衡状态下的平衡因子存在2(右侧高度减左侧高度)，那么就相当于根结点的右子结点的添加一个元素，通过比较右子结点两侧高度来判断，如果左侧高于右侧就进行右左旋，如果右侧高于或等于左侧就进行左旋。
      
    • 如果删除元素在根结点的右侧，通过以根结点的右子结点为新的根结点进行判断实现递归操作。因为在删除元素之前，整棵树都是平衡的，所以每个结点的平衡因子都是0或1或-1，而在删除元素之后，导致整棵树不平衡，但是也只会出现不平衡状态下的平衡因子存在-2(右侧高度减左侧高度)，那么就相当于根结点的左子结点的添加一个元素，通过比较左子结点两侧高度来判断，如果左侧高于右侧就进行右旋，如果右侧高于或等于左侧就进行左右旋。
      
    • 如果删除元素是根结点，那么如果根结点的左侧右侧均不为空的话，如果左子树高于右子树那么从左子树中找寻最大元素；如果右子树高于左子树那么从右子树找寻最小的元素。这种方法避免旋转，因为无论是在左子树内找最大的还是在右子树中找寻最小元素替代，这两种元素的都只是叶结点，在未删除之前已经平衡好，平衡因子只能为0，所以替代之后也为平衡树。
    • 如果删除元素是根结点，那么如果根结点没有右子结点，那么左子结点成为新的左结点；那么如果根结点没有左子结点，那么右子结点成为新的根结点。
      

代码托管

上周考试错题总结

上周无错题...

结对与互评

点评(王禹涵)

• 博客中值得学习的或问题：
  • 背景图很好看，还是截图内容看得不清晰，建议换个背景图。
• 代码中值得学习的或问题：
  • 代码图片也是看的不清晰，下次尝试用电脑做出的框图来尝试。
• 基于评分标准，我给本博客打分：8分。
  • 得分情况如下：
  • 正确使用Markdown语法（加1分）
  • 模板中的要素齐全（加1分）
  • 教材学习中的问题和解决过程, 三个问题加3分
  • 代码调试中的问题和解决过程, 一个问题加1分
  • 感想，体会不假大空的加1分
  • 点评认真，能指出博客和代码中的问题的加1分

点评(方艺雯)

• 博客中值得学习的或问题：
  • 图片特别细致，但是针对那一大串代码建议配一些讲解，建议不要全放到代码注释中。
• 代码中值得学习的或问题：
  • 代码问题没有看到。
• 基于评分标准，我给本博客打分：6分。
• 得分情况如下：
  • 正确使用Markdown语法（加1分）
  • 教材学习中的问题和解决过程, 三个问题加3分
  • 代码调试中的问题和解决过程, 无个问题加0分
  • 感想，体会不假大空的加1分
  • 点评认真，能指出博客和代码中的问题的加1分

互评对象

• 本周结对学习情况
  20172314方艺雯
  20172323王禹涵

• 结对学习内容：平衡二叉树(AVL树和红黑树)

感悟

第十一章的二叉查找树学起来比树还难学，欲哭无泪。二叉查找树的添加和删除与有序列表的添加删除差不多，每添加一个就要判断一次还要看平不平衡，不平衡的话还得给它弄平衡了，还有红黑树的方法，感觉都绕晕了，特别懵，递归和迭代，吐血(绝望)...

学习进度条

参考资料

• AVL

20172305 2018-2019-1 《Java软件结构与数据结构》第七周学习总结

标签：链表实现   迭代   相等   search   解决   eal   错题   代码调试   数据结构   

原文地址：https://www.cnblogs.com/sanjinge/p/9898501.html