标签:代码 优秀 图表 测试 i++ col add int 交集
在上周的算法设计课程中,我们学习了UNION-FIND算法,该算法用来对不相交集进行查询与合并操作,但任何优秀的算法都必须要用实际的代码来进行实现,接下来我们就来看看具体的代码实现
一般来说,对于一个不相关集A = {1, 2, ..., n} 来说,我们使用两个长度为n的数组p[] 和 rank[] 来表示。
p[] 中,数组下标表示所对应的元素,数组值表示该元素对应的父节点,没有父节点时值为0,如a[1] = 2 便表示元素1的父节点为2
rank[] 表示数组元素的秩,一般用来表示该节点的高度,初始值全为零。
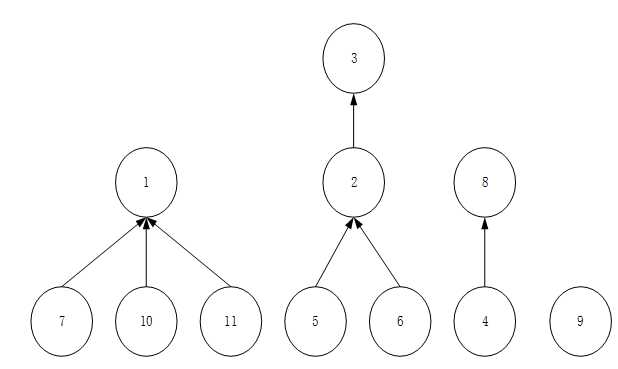
上图的不相交集结构用数组表示为下图:
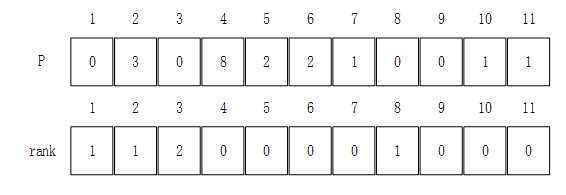
UNION-FIND算法包含两个方法FIND(x) 与 UNION(x, y)
FIND(x):用来寻找包含x的根,算法如下(书P83)
UNION(x, y):用来合并两个树,算法如下(书P83)
具体代码实现如下:
1 //不相交集及union-find算法的练习 2 public class Gather { //声明不相交集类 3 private int p[] = new int[50]; //存放元素父节点 4 private int rank[] = new int[50]; //存放元素的秩 5 public int length; //不相交集的长度 6 public Gather(int length) 7 { 8 this.length = length; 9 } 10 //寻找指定结点 11 public int find(int n) 12 { 13 int i = n; 14 /*这里的i,n 分别对应书上算法中的y,x 15 * 同理union中的a,b对应书上算法的u,v*/ 16 int root, t; 17 while(p[i]!=0) 18 //向上寻找根结点 19 i = p[i]; 20 root = i; 21 i = n; //两个指针分别指向根结点与初始结点 22 while(p[i]!=0) 23 { 24 //执行路径压缩 25 t = p[i]; //t指向i的父节点 26 p[i] = root; //将i的父节点设为根结点 27 i = t; //指针上移 28 } 29 return root; 30 } 31 //将两个树合并 32 public void union(int x,int y) 33 { 34 int a = find(x); 35 int b = find(y); 36 //当a的秩小于等于b的秩时,以b作为父结点 37 if(rank[a] <= rank[b]) 38 { 39 p[a] = b; 40 //当a的秩等于b的秩时,b的秩+1 41 if(rank[a] == rank[b]) 42 rank[b]++; 43 } 44 else p[b] = a; //当a的秩大于b的秩时,a作为父节点 45 } 46 //输出不相交集 47 public void dispGather() 48 { 49 System.out.print("元素值:"); 50 for(int i=1;i<length;i++) 51 System.out.print(i + " "); //输出所有元素 52 System.out.println(); 53 System.out.print("父节点:"); 54 for(int i=1;i<length;i++) 55 System.out.print(p[i] + " "); //输出所有元素对应的父节点值 56 System.out.println("\n"); 57 } 58 }
写好了代码,我们需要用一些数据来测试一下我们的代码,我们采用书上P83的例4.4作为实例。
例4.4 设S = {1, 2, ..., 9},考虑用下面的合并和寻找序列:UNION(1, 2), UNION(3,4), UNION(5,6), UNION(7,8), UNION(2,4), UNION(8,9), UNION(6,8), FIND(5), UNION(4,8), FIND(1)

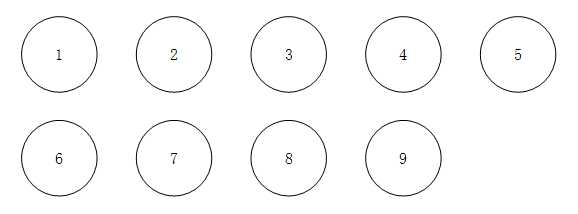
创建一个Gather对象并输出其初始状态(需要注意的是,我们的算法是下标从1开始的,而java中数组是从下标0开始的,所以我们定义长度为n的不相交集时,输入数字必须为n+1)

结果图表示如下:

由于篇幅关系,我们就不像书上和代码上那样分步看结果了,直接跳到最后的输出:

用图表示如下:
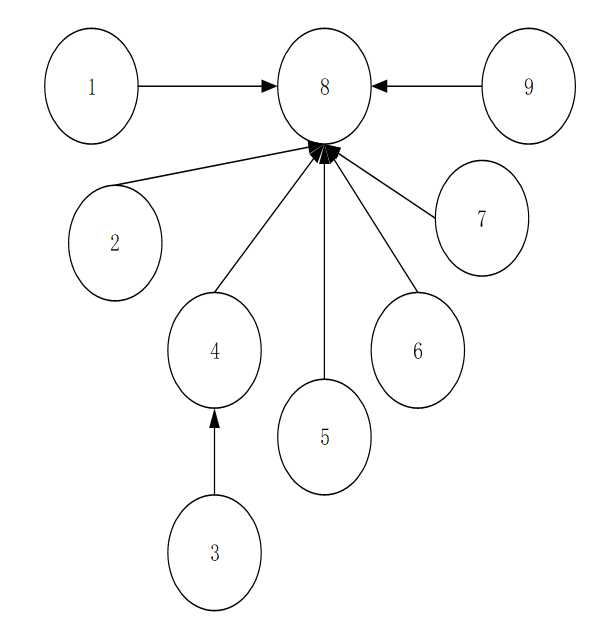
标签:代码 优秀 图表 测试 i++ col add int 交集
原文地址:https://www.cnblogs.com/sunriseblogs/p/9936774.html