标签:length 调整 数组 序列 fun 分享图片 大小 inf 大于
1.冒泡排序
思想:同过比较相邻两个的值,一趟排序后将最大值max放在最右端,再经过一趟排序将次大值排在max左边,依此数次排序后得到一个有序数组。
算法平均复杂度:O(n2)。
是否稳定:稳定。
public class BubbleSort { public static void sort(int []arr){ for(int i=0;i<arr.length-1;i++){//外部循环控制排序趟数 for(int j = 0;j<arr.length-1-i;j++){//内部循环决定每一趟比较次数 if(arr[j]>arr[j+1]){ //升序 int temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } } } public static void main(String[] args) { int[] arr = {8,2,1,6,7,3,4,0}; sort(arr); System.out.println(Arrays.toString(arr)); } }
2.快速排序
思想:采用分治的思想。首先选取一个基准元素,经过一趟排序之后,将比基准元素小的放在其左边,比基准元素大的放在其右边,将数组分成两部分。对于左边的部分,再选取一个基准元素将棋再分为两部分,右边同样如此。如此,多躺排序之后得到一个有序数列。
算法平均复杂度:O(NlogN)
是否稳定:不稳定
public class QuickSort { public static void main(String[] args) { int a[]={1,4,3,8,5,9,6}; QuickSort(a, 0, 6); for (int i : a) { System.out.println(i); } } public static void QuickSort(int a[],int p,int r){ if(p<r){ int q = Partition(a, p, r); QuickSort(a, p, q-1); QuickSort(a, q+1, r); } } public static int Partition(int a[],int p,int r){ int i = p,j =r+1; int x = a[p]; while(true){ while(a[++i]<x &&i<r ); while(a[--j]>x); if(i>=j) break; Swap(a,i,j); } a[p] = a[j]; a[j] = x; return j; } public static void Swap(int a[],int i, int j){ int temp; temp = a[i]; a[i] = a[j]; a[j] = temp; } }
3.堆排序
思想:将数组元素构造成大顶推或小顶堆,然后将堆定元素与堆尾元素交换,再重构大顶堆,将堆顶元素与堆尾交换。重复数次后形成有序数列。
算法平均复杂度:O(nlogn)
是否稳定:不稳定。
public class Heapsort { public static void main(String []args){ int []arr = {0,8,7,6,9,10,3,2,1}; sort(arr); System.out.println(Arrays.toString(arr)); } public static void sort(int []arr){ //1.构建大顶堆 for(int i=arr.length/2-1;i>=0;i--){ //从第一个非叶子结点从下至上,从右至左调整结构 adjustHeap(arr,i,arr.length); } //2.调整堆结构+交换堆顶元素与末尾元素 for(int j=arr.length-1;j>0;j--){ swap(arr,0,j);//将堆顶元素与末尾元素进行交换 adjustHeap(arr,0,j);//重新对堆进行调整 } } public static void adjustHeap(int []arr,int i,int length){ int temp = arr[i];//先取出当前元素i for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始,也就是2i+1处开始 if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点,k指向右子结点 k++; } if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换) arr[i] = arr[k]; i = k; }else{ break; } arr[i] = temp;//将temp值放到最终的位置 } } public static void swap(int []arr,int a ,int b){ int temp=arr[a]; arr[a] = arr[b]; arr[b] = temp; } }
4.插入排序
思想:从待排序的序列中选择一个元素,将其插入到已排序好的元素序列中 ,重复上述步骤直到待排序序列中没有元素为止。
复杂度:O(n2)
是否稳定:稳定
public class InsertSort { public static void insertSort(int a[],int len){ for(int i=1;i<len;i++){//因为我们要对该待排序列的每一个元素都和前面的已排好序的序列进行插入,所以我们会对序列进行遍历 for(int j=0;j<i;j++){//第二层循环主要用于对已排好序的序列进行扫描,和要插入进来的数据进行逐一比较,然后决定插入到哪里 if(a[j]<a[i]){//从前往后对已排好序的元素和待插入元素进行大小比较,然后直到找到一个元素比被插入元素大,则交换位置 int temp = a[i]; a[i] = a[j]; a[j] = temp; } } } } public static void main(String[] args) { int[]a ={1,3,5,2,7,6,9,8}; insertSort(a, a.length); System.out.println(Arrays.toString(a)); } }
5.选择排序
思想:在未排序的序列中选择最小的元素,放在已排序的队列首部,然后再从未排序的序列中选择最小的放到以排序的队列中去。以此重复,知道未排序的序列没有元素为止。
平均复杂度:O(n2)
是否稳定:不稳定
function selectionSort(arr) { var len = arr.length; var minIndex, temp; for (var i = 0; i < len - 1; i++) { minIndex = i; //每次都从已排序序列的末尾后一位开始 for (var j = i + 1; j < len; j++) { if (arr[j] < arr[minIndex]) { //寻找最小的数 minIndex = j; //将最小数的索引保存 } } //放到已排序序列的末尾(即交换),该操作很有可能把稳定性打乱,所以选择排序是不稳定的排序算法 temp = arr[i]; arr[i] = arr[minIndex]; arr[minIndex] = temp; } return arr; }
6.归并排序
思想:归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
public class MergeSort { public static void main(String []args){ int []arr = {9,8,7,6,5,4,3,2,1}; sort(arr); System.out.println(Arrays.toString(arr)); } public static void sort(int []arr){ int []temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间 sort(arr,0,arr.length-1,temp); } private static void sort(int[] arr,int left,int right,int []temp){ if(left<right){ int mid = (left+right)/2; sort(arr,left,mid,temp);//左边归并排序,使得左子序列有序 sort(arr,mid+1,right,temp);//右边归并排序,使得右子序列有序 merge(arr,left,mid,right,temp);//将两个有序子数组合并操作 } } private static void merge(int[] arr,int left,int mid,int right,int[] temp){ int i = left;//左序列指针 int j = mid+1;//右序列指针 int t = 0;//临时数组指针 while (i<=mid && j<=right){ if(arr[i]<=arr[j]){ temp[t++] = arr[i++]; }else { temp[t++] = arr[j++]; } } while(i<=mid){//将左边剩余元素填充进temp中 temp[t++] = arr[i++]; } while(j<=right){//将右序列剩余元素填充进temp中 temp[t++] = arr[j++]; } t = 0; //将temp中的元素全部拷贝到原数组中 while(left <= right){ arr[left++] = temp[t++]; } } }
总结
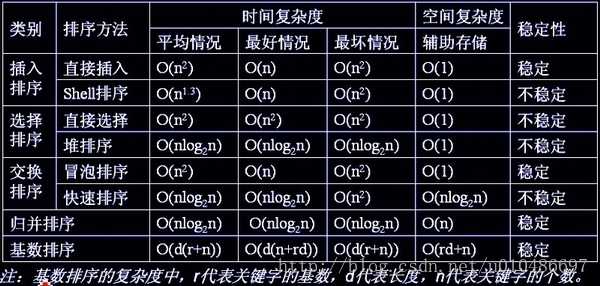
标签:length 调整 数组 序列 fun 分享图片 大小 inf 大于
原文地址:https://www.cnblogs.com/menbo/p/9717849.html