标签：tchar   int   ios   pac   [1]   for   前缀   分享   alt   

树状数组的区间更新

思路

树状数组的区间更新：
首先引入一个差分数组：
差分数组：令d[i]=a[i]-a[i-1];
a[i]=∑d[i];
即可以得到：

∑a[k]=d[1]+d[1]+d[2]+d[1]+d[2]+d[3]+...+d[1]+d[2]+d[3]+...+d[k]
=∑(k-i+1)*d[i](i从1到k)

变化得到：
(重要)

∑a[k]=∑( k + 1 ) * d[i] - i * d[i](i从1到k)

(重要)

根据d的定义，对[l,r]区间加上x，那么a[l]和a[l-1]的差增加了x，a[r+1]与a[r]的差减少了x，所以就对差分数组的前缀和进行修改
设c是差分数组的前缀和
d[i]可以用前缀和维护，i * d[i]也可用前缀和维护。
令c1为d[i]前缀和,c2为i * d[i]前缀和。

区间更新：

void update(int x,LL v){
    for(int i=x;i<=n;i+=lowbit(i)){
        c1[i]+=v;
        c2[i]+=x*v;
    }
}
//对于[l,r]加上v 那么a[l]和a[l-1]的差增加了v 
//             a[r+1]与a[r]的差减少了v 
update(l,v);update(r+1,-v);

区间查询：

LL query(int x){
    LL ans=0;
    for(int i=x;i>0;i-=lowbit(i)) ans+=(x+1)*c1[i]-c2[i];
    return ans;
}

A simple problem with integer 2

题目描述

思路

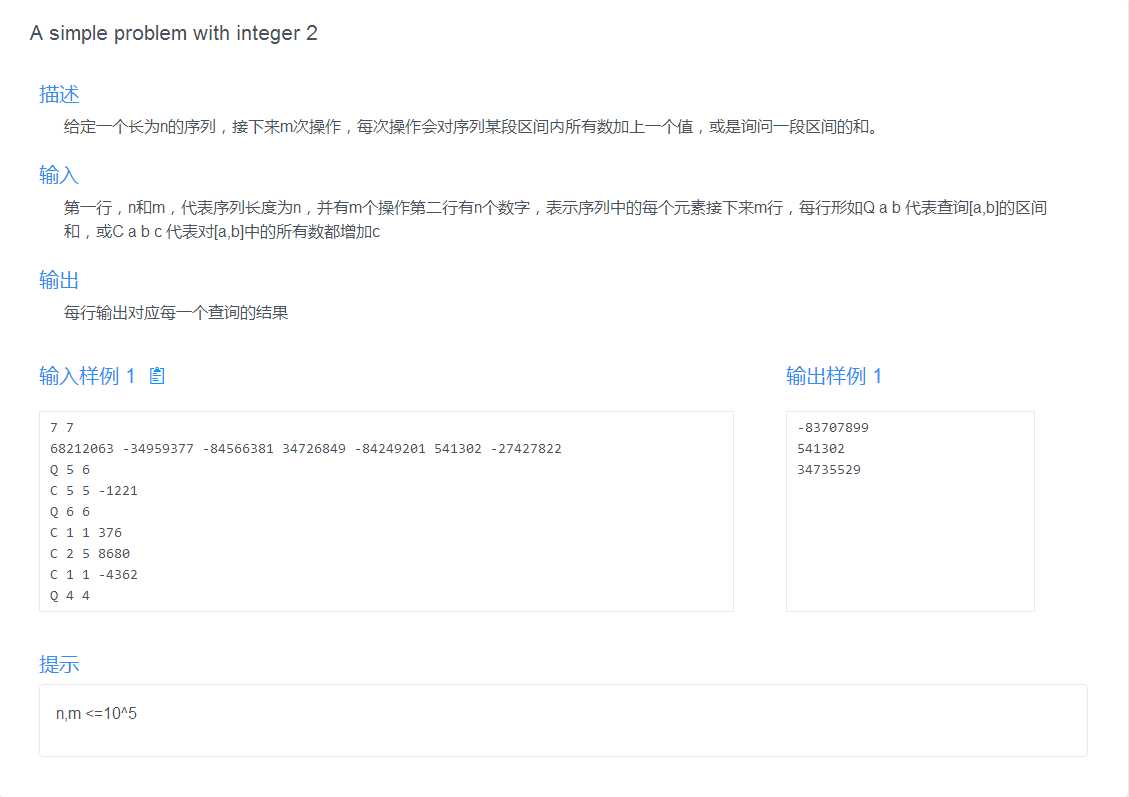
树状数组区间更新板子题

代码

#include <cstdio>
#include <iostream>
#define LL long long
using namespace std;
const int maxn=1e5+5;
LL n,m;
LL a[maxn];
LL c1[maxn],c2[maxn];
void read(long long &n){
    long long num=0;int w=1;
    char ch=getchar();
    while(ch>'9'||ch<'0'){
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        num=num*10+ch-'0';
        ch=getchar();
    }
    n=num*w;
}
int lowbit(int x){return x&(-x);}
void update(int x,LL v){
    for(int i=x;i<=n;i+=lowbit(i)){
        c1[i]+=v;
        c2[i]+=x*v;
    }
}
LL query(int x){
    LL ans=0;
    for(int i=x;i>0;i-=lowbit(i)) ans+=(x+1)*c1[i]-c2[i];
    return ans;
}
int main(){
    read(n);read(m);
    for(int i=1;i<=n;i++){
         read(a[i]);
         update(i,a[i]-a[i-1]);
    }
    for(int i=1;i<=m;i++){
        char ch;cin>>ch;
        long long a,b;read(a);read(b);
        if(ch=='Q') printf("%lld\n",query(b)-query(a-1));
        else{
            long long v;read(v);
            update(a,v);update(b+1,-v);
        }
    }
    return 0;
}

1zojP5021 A simple problem with integer 2|板子|树状数组的区间更新

标签：tchar   int   ios   pac   [1]   for   前缀   分享   alt   

原文地址：https://www.cnblogs.com/saitoasuka/p/9977123.html