标签：解决   表示   记录学习   生成树   a算法   解决方案   队列   联通   矩阵   

2018-2019-20172321 《Java软件结构与数据结构》第九周学习总结

教材学习内容总结

第15章 图

无向图

• 图由顶点和边组成。
  • 顶点由名字或标号来表示，如：A、B、C、D；
  • 边由连接的顶点对来表示，如：（A,B）,（C,D），表示两顶点之间有一条边。
• 无向图：与树类似，图也由结点和这些结点之间的连接构成。这些结点是顶点，而结点之间的链接是边。无向图是一种边为无序结点对的图。于是，记做（A,B）的边就意味着A与B之间有一条从两个方向都可以游历的连接。边记作（A,B）和记作（B,A）的含义是完全一样的。

• 邻接（邻居）：两个顶点之间有边连接。
• 自循环（悬挂）：自己连接到自己的边。
• 完全图：含有最多 条边的无向图。例如：

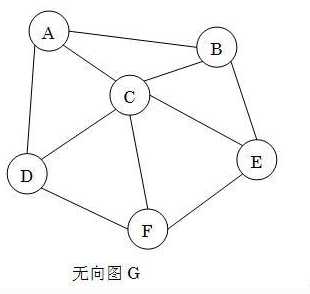
无向图G是一个完全图。

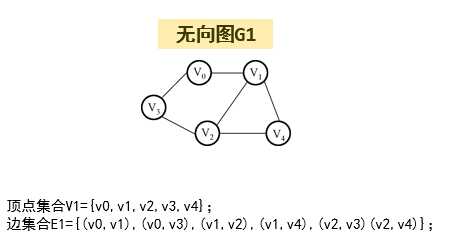
• 路径：连接图中两个顶点的边的序列，可以由多条边组成。

  无向图中的路径是双向的。

• 路径长度：路径中所含边的数目（顶点个数减1 ）。

• 连通图：无向图中 任意两个顶点间都有路径。例如：

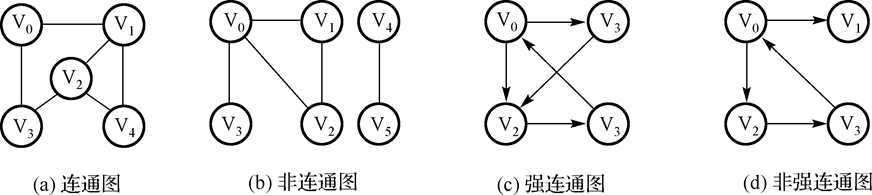
完全图一定是连通图，连通图不一定是完全图。

• 环（回路）：第一个顶点与最后一个顶点相同且没有重复边的路径。例如：

• 无环图：没有环的图。
• 子图：类似集合中“子集”的概念，示例如下：

其中，（b），（c）是（a）的子图。

• 生成树：包含无向图G1所有顶点的极小连通子图称为G1的生成树。例如：

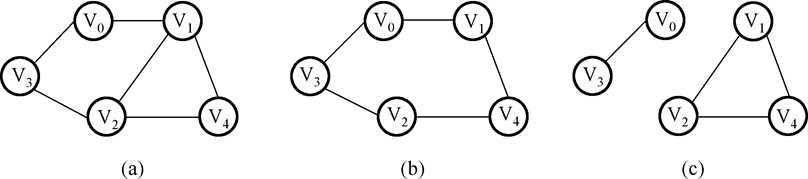
• 稀疏图与稠密图：有很少条边或弧（如 e < n lognn，n 是图的顶点数，e 是弧数）的图称为稀疏图，反之称为稠密图。

有向图

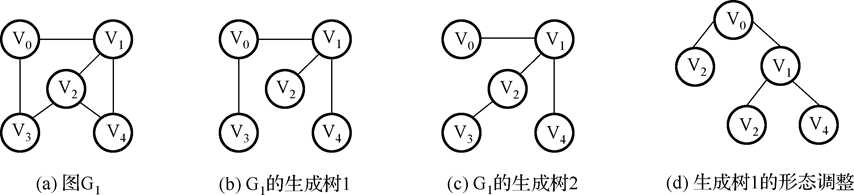
• 有向图：顶点之间有序连接，边是顶点的有序对。

  边（A,B）和（B,A）方向不同。

• 有向路径：连接两个顶点有向边的序列。

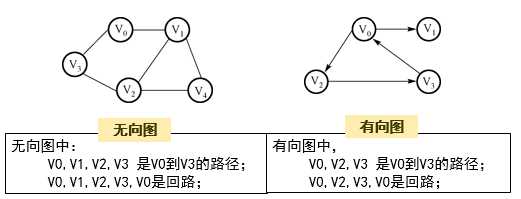
• 有向图中的有序对常用序偶表示，例如：

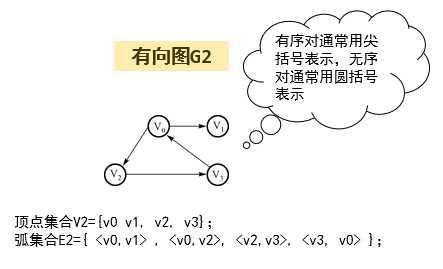
上图中路径 V00→V22→V33 是从V00到V33的路径，但是反过来不再成立。

• 注意连通有向图与无向图不同，有向边决定连通性。例如：

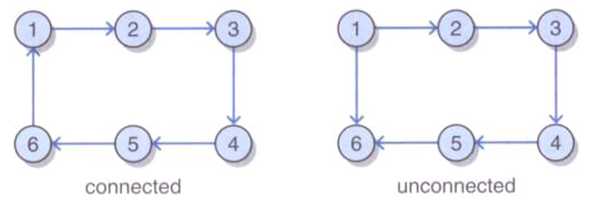
上图中左图为联通图，右图不联通，因为从任何顶点到顶点1都没有路径。

• 有向树是一个有向图，其中指定一个元素为根，则具有下列特性：

  任何顶点到根都没有连接。

到达每个非根元素的连接都只有一个。

从根到每个顶点都有路径。

• 顶点的度、出度、入度：

网络

• 网络：（加权图）是一种每条边都带有权重或代价的图。

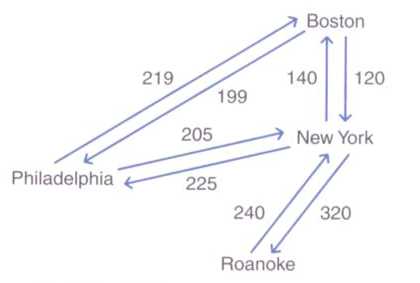
网络可以是无向的也可以是有向的。

常用图的算法

• 遍历

• 广度优先遍历：类似于树的层序遍历， 从一个顶点开始，辐射状地优先遍历其周围较广的区域。

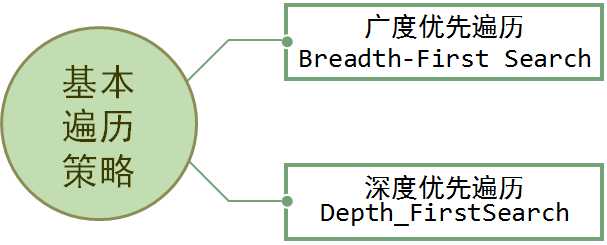
• 深度优先遍历：图的深度优先搜索，类似于树的先序遍历， 所遵循的搜索策略是尽可能“深”地搜索图。

  图的深度优先遍历与广度优先遍历的唯一不同是，他使用的是栈而不是队列来管理遍历。

• 连通性：从任意结点开始的广度优先遍历中得到的顶点数等于图中所含顶点数。
• 生成树：包含图中所有顶点及图中部分边的一棵树。
• 最小生成树：所含边权值之和小于其他生成树的边的权值之和。
  • 因为树总是图，对于有些图来说，图本身就是一颗生成树，所以这样的图的生成树中将包含全部的边。
  • 最小生成树是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树。

通常构造最小生成树的算法有两种：

① Prim算法： ① Prim算法： ① Prim算法：
它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

② Kruskal算法： ② Kruskal算法： ② Kruskal算法：
假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

• 判定最短路径：
  • 判定起始顶点和目标顶点之间是否存在最短路径（两个顶点之间边数最少的路径）。
  • 在带权图中找到最短路径。（Dijkstra算法）

图的实现策略

• 邻接矩阵：

教材学习中的问题和解决过程

• 问题1：问题是有向图和无向图的广度遍历的区别
• 问题1解决方案：根据我查的资料显示是不一样的，但是再向图中从出发的顶点没有路径的顶点也要写出来，这不是找所有的路径而是遍历所以不能漏掉任何一个元素。

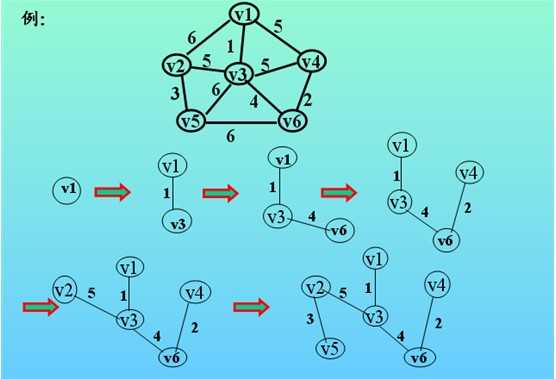
我看到一个大佬的博客解决了这个问题，而且我阅读之后也有了比较深刻的理解
大佬的博客————图的深度优先遍历和广度优先遍历理解

代码调试中的问题和解决过程

• 问题1：先是在用邻接矩阵实现无向图的补全，前面的都一切OK，该输出的基本上都输出了，但是在最后出现了一个空指针问题

• 问题1解决方案：之后发现，是当时写程序的时候不够严谨，结果这个变量为空的，但是我当时没有去注意就直接使用，就出现NullPointException。
• 问题2：在实现pp15.1的时候，出现了一个数组越界异常，这就没道理了啊

• 问题2解决方案：不断往上追溯，最后发现好像是之前的一个类里面的遗留问题，当时没注意到，这个类的在这里被使用就出问题了

代码托管

上周考试错题总结

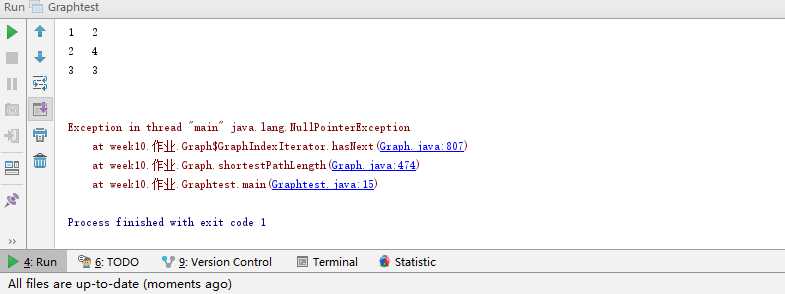
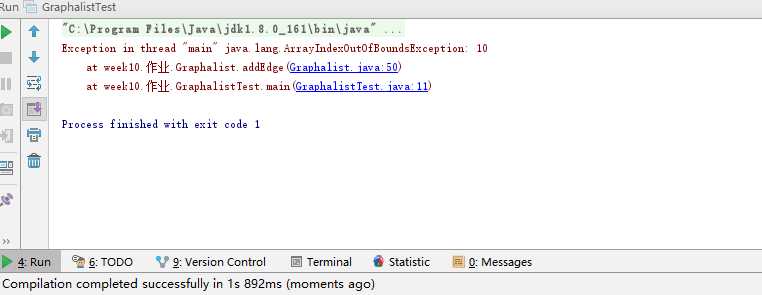
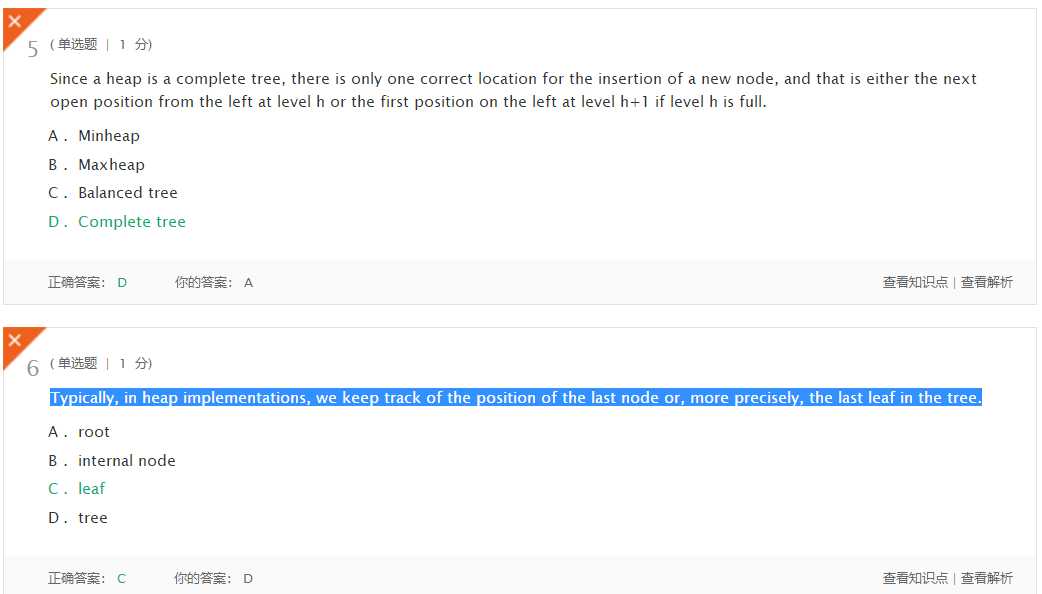
这两道题改了选项，我当时没注意到群里面的，好气哦

结对及互评

• 20172324曾程
• 博客中值得学习的或问题：
  • 书上代码的学习很到位
  • 代码调试环节比较详细，从截图上来看注释也很规范整齐，值得学习。
• 基于评分标准，我给本博客打分：11分。得分情况如下：
  • 正确使用Markdown语法（加1分）
  • 模板中的要素齐全（加1分）
  • 教材学习中的问题和解决过程, 加4分
  • 代码调试中的问题和解决过程, 加4分
  • 本周有效代码超过300分行，加2分
  • 进度条中记录学习时间与改进情况的加1分

学习进度条

参考资料

• 《Java软件结构与数据结构》第四版
• 邻接表的实现原理
• 图的邻接矩阵的实现

2018-2019-20172321 《Java软件结构与数据结构》第九周学习总结

标签：解决   表示   记录学习   生成树   a算法   解决方案   队列   联通   矩阵   

原文地址：https://www.cnblogs.com/N-idhogg/p/9959916.html