标签:下标 关系 递归 逻辑 位置 def 此刻 最大的 直接
1、(二叉)堆可以使用一个数组实现,在逻辑上,我们可以将这个数组实现成一个完全二叉树。因为完全二叉树的父节点和孩子节点之间存在关系。例子如下:
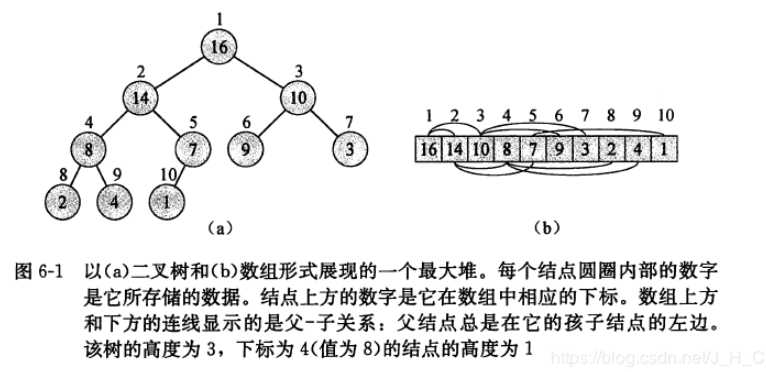
图a中就是一棵完全二叉树,并且这个完全二叉树是一个二叉最大堆(max堆)结构。因为该完全二叉树所有节点都满足堆序性。图b是该最大堆在内存上的存储形式,即以数组的形式存储,可以通过数组下标来实现其逻辑结构最大堆。
2、二叉堆要满足两个性:结构性和堆序性。
1)结构性:即其逻辑结构是一个完全二叉树。
2)堆序性:如果是最大堆,则其父节点的值要大于等于孩子节点的值;如果是最小堆,则其父节点必须小于等于其
孩子节点。
3、堆化:当堆中有节点不符合堆序性,需要移动其位置,保持堆的堆序性
1)在《算法导论》P86页中,其堆化使用的是递归,过程如下图(下面的是最大堆化过程)

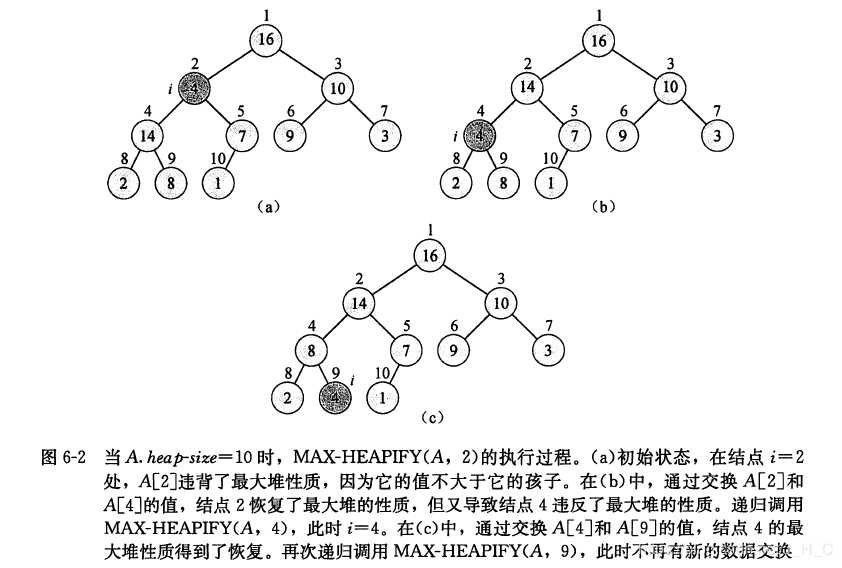
即以i为父节点,加上其孩子节点构成一个局部子树。在这个局部子树中,我们判断该局部子树是否构成一个最大堆。先找出父节点、左孩子节点和右孩子节点中的最大值,并将其下标保存到largest中。比较largest与 i 相等,说明A[i]就是最大值,该局部子树就是最大堆。如果largest与 i 不相等,说明A[i]不是最大值,将A[largest]与A[i]进行交换。此时,这个局部子树就是最大堆了。不过需要注意的是此时A[largest]是之前局部子树父节点的值A[i],而largest是之前局部子树的孩子节点,这意味着可能会破坏以largest下标作为父节点的局部子树的堆序性,所以需要递归的对以largest下标作为父节点的局部子树进行堆化操作。例子如下图:
对于一个树高为h的节点来说,堆化的时间复杂度为O(h)。也就是说堆化的时间复杂度和节点所在的高度成线性关系。所以对于z总节点数为N的完全二叉树,堆化其根节点所需要的时间是O(logN)
其代码实现如下:
#define LEFT(i) (2 * i)
#define RIGHT(i) (2 * i + 1)
void MaxHeapify(int a[], int i, int len)
{
int left = LEFT(i);
int right = RIGHT(i);
int largest = i;
if (left < len && a[left] > a[largest])
largest = left;
if (right < len && a[right] > a[largest])
largest = right;
if (largest != i)
{
//使用异或操作实现两个数交换,不需要中间变量,这种交换方法在两个值相等时会出错,全部为0
//证明:a,b交换,其步骤为:a = a ^ b; b = a ^ b; a = a ^ b;
//第二步: b = (a ^ b) ^ b = a ^ (b ^ b) = a ^ 0 = a
//第三步:a = (a ^ b) ^ a = (a ^ a) ^ b = 0 ^ b = b
a[largest] = a[largest] ^ a[i];
a[i] = a[largest] ^ a[i];
a[largest] = a[largest] ^ a[i];
//也可以使用数学操作来完成两个数交换,不使用中间变量,这种交换方法在两个值相等时会出错为0
//a[largest] = a[largest] + a[i];
//a[i] = a[largest] - a[i];
//a[largest] = a[largest] - a[i];
MaxHeapify(a, largest, len);
}
}
2)在《数据结构与算法分析:C语言描述》p172中,堆化使用的是循环,两者的原理类似,只有小部分不同,比如这里堆的数组实现是从数组下标0开始的,不是从数组下标1开始的。其代码实现如下
//实现将二叉堆中的节点下滤,这个二叉堆中根节点是最大值,i是需要下滤的堆节点,len是数组的长度
void PercolateDown(int a[], int i, int len)
{
int tmp;//tmp是用来存储要下滤的堆节点的值
//书中的二叉堆是从数组下标1开始存储根节点,所以其下标满足完全二叉树的规律即左孩子节点在数组中的下标等于父亲节点在数组的下标乘2.
//而这里是从数组下标为0的位置开始存储根节点,所以其下标之间的关系为左孩子节点在数组中的下标等于父亲节点在数组的下标乘2加1.
int child_index = 2 * i + 1;
for (tmp = a[i]; child_index < len; )
{
//当右孩子节点值大于左孩子节点值,那么就需要把右孩子节点值拿出来和父节点比较,原则是拿孩子节点中最大的值进行比较
if (child_index != len - 1 && a[child_index + 1] > a[child_index])
child_index++;
if (tmp < a[child_index])//此刻的a[i]是个没用的值,它和其父节点的值相同。这里必须使用tmp也就是要下滤的堆节点值
a[i] = a[child_index];
else//如果tmp比子节点大,那意味着这个位置就是要符合堆序性的位置
break;
i = child_index;//进入到下一层,即之前的孩子变成了父节点,现在的孩子是之前节点的孙子
child_index = 2 * i + 1;//找出现在节点的孩子
}
//循环结束就能找到不破坏堆序性的位置来插入堆最后一个节点,因为删除根节点为了
//不破坏堆的完全二叉树结构(结构性),需要将最后一个堆节点插入到合适的位置形成新的堆
a[i] = tmp;
}
除了这里使用的是循环外,在处理局部子树不满足堆序性时,只是将孩子节点的最大值赋给了局部子树的父亲节点,而没有将父节点的值赋给该孩子节点,所以就不能使用a[i]来进行比较。这里是将一开始要堆化的节点a[i]保存起来,然后使用这个值和后面循环中的新的局部子树的最大孩子节点比较。
4、创建堆
创建堆都是从完全二叉树的非叶子节点开始堆化每个局部子树。对于《数据结构与算法分析:C语言描述》中来说长度为len的数组a,其元素a[len/2 + 1]、a[len/2 + 2]......都是完全二叉树的叶子节点,因为其从下标为0的位置开始存储堆的节点,数组长度就是堆的节点数。而对于《算法导论》,其是从数组下标为1的位置开始存储堆节点,所以长度为len的数组a,其堆节点总数heap_size = len - 1,所以数组元素a[heap_size/2 + 1]、a[heap_size/2 + 2]......才是完全二叉树的叶子节点。创建堆的时间复杂度为O(N),n是树总的节点数,具体证明参考《算法导论》p88页。
如果使用的是《算法导论》中的递归堆化方法,其代码如下:
void BuildMaxHeap(int a[], int len)
{
int heap_size = len - 1;
for (int i = heap_size / 2; i > 0; i--)
{
MaxHeapify(a, i, len);
}
}
如果使用的是《数据结构与算法分析:C语言描述》中的循环堆化方法,其代码如下:
for (i = len / 2; i >= 0; i--)//数组下标大于len/2的全都是叶子节点
{
PercolateDown(a, i, len);
}
5、堆排序
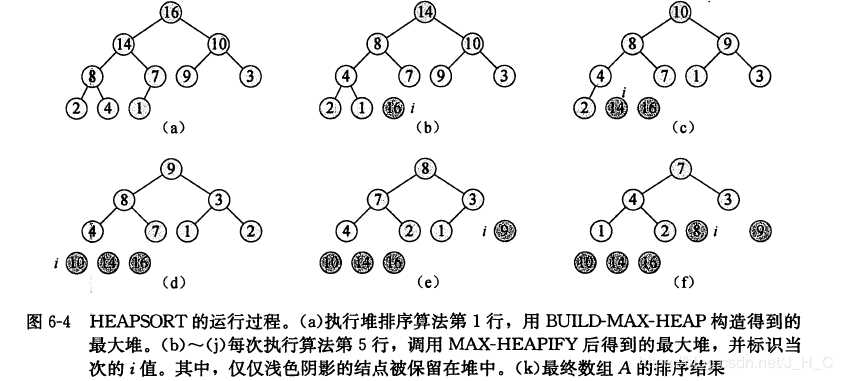
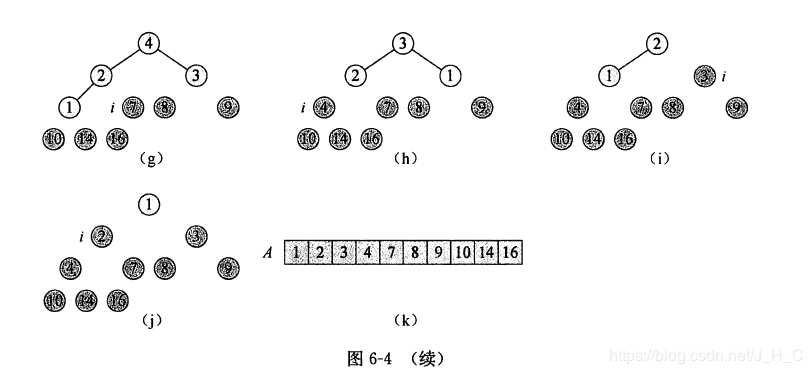
堆排序的思路很简单,就是将最大堆中的根节点即最大的元素删除,堆化形成新的堆,此时删除根节点前的堆的最后一个节点不属于新的堆,因此可以将删除的根节点值保存到该节点中。在程序实现中就是直接将最后一个元素和根节点元素交换,然后堆大小减1,堆化形成新的堆。 堆排序的时间复杂度为O(nlogn),n为堆的节点数。例子如下:
使用《算法导论》中的函数,堆排序代码实现如下:
void HeapSort(int a[], int len)
{
//int heap_size = len - 1;//是从数组下标1开始存储堆元素的
BuildMaxHeap(a, len);
//注意i到2就排好序了,这里由于下面交换数值不允许是相同的值,所以只能到2
for (int i = len - 1; i > 1; i--)
{
//交换根节点和最后节点元素值,这种交换方法在两个值相等时会出错,全部为0
a[1] = a[1] + a[i];
a[i] = a[1] - a[i];
a[1] = a[1] - a[i];
MaxHeapify(a, 1, i);
}
}
使用《数据结构与算法分析:C语言描述》中的函数代码如下:
void HeapSort(int a[], int len)
{
int i;
//先构建二叉堆
for (i = len / 2; i >= 0; i--)//数组下标大于len/2的全都是叶子节点
{
PercolateDown(a, i, len);
}
for (i = len - 1; i > 0; i--)
{
//不用中间变量,交换两个变量的值
a[0] = a[0] + a[i];
a[i] = a[0] - a[i];
a[0] = a[0] - a[i];
PercolateDown(a, 0, i);
}
}
在主函数中调用《算法导论》的堆排序函数进行堆排序:
int main()
{
int a[11] = { 0, 14, 16, 1, 8, 3, 9, 7, 2, 4, 10 };//第一个元素不是我们要排序的序列
for (int i = 1; i < 11; i++)
{
cout << a[i] << " ";
}
cout << endl;
HeapSort(a, 11);
cout << "堆排序之后的结果:" << endl;
for (int i = 1; i < 11; i++)
{
cout << a[i] << " ";
}
system("pause");
return 0;
}
运行结果:
在主函数中调用《数据结构与算法分析:C语言描述》中的堆排序函数:
int main()
{
int a[10] = { 14, 16, 1, 8, 3, 9, 7, 2, 4, 10 };
for (int i = 0; i < 10; i++)
{
cout << a[i] << " ";
}
cout << endl;
HeapSort(a, 10);
cout << "堆排序之后的结果:" << endl;
for (int i = 0; i < 10; i++)
{
cout << a[i] << " ";
}
system("pause");
return 0;
}
运行结果:
---------------------
作者:flychildc
来源:CSDN
原文:https://blog.csdn.net/J_H_C/article/details/84373412
版权声明:本文为博主原创文章,转载请附上博文链接!
标签:下标 关系 递归 逻辑 位置 def 此刻 最大的 直接
原文地址:https://www.cnblogs.com/flychildc/p/10007901.html