标签:ret ddd 方式 存储空间 return iostream alt 技术 初始化
最近有很多的小朋友问我什么是哈夫曼编码,哈夫曼编码是一种可变字长的编码,那什么是可变字长呢?就是一句话里的每一个字符(ASCII码)它的位数(长度)是不一样的。就像我们一句话(AAAACCCCCDDDDBBE)有A,B,C,D,E五种字符,在这里我们可以用01表示A字符,用001表示B字符,用11表示C字符,用10表示D字符,用000表示E字符。如下图: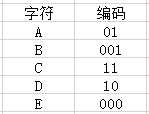
既然知道了哈夫曼编码是什么了,那又有好奇的小朋友又会问了:那么哈夫曼编码是按照什么原理生成的呢?
在这里我就要告诉大家,哈夫曼编码是根据哈夫曼树生成的,如果看到这里有小朋友不知道什么是树的话可以先去学习一下二叉树。哈夫曼树是一种特殊的二叉树,为什么特殊?因为哈夫曼树只有叶子节点保存了数据。
那接下来我们就来分析怎么去对一句话的每一个字符生成编码:
以前的编码方式就是根据一句话中不同字符的个数,来确定字符编码的长度,然后按照一定的顺序对字符进行唯一的编码。这样虽然简单,但也造成了数据存储空间的高占用。哈夫曼编码就是为了解决高占用的问题,从原来的基础上缩短一句话的长度,可能有数学好的小朋友们已经猜到了,一句话中,绝大多数情况下每个字符出现的概率是不一样的,竟然概率不一样,那么我们不就可以让出现概率高的字符更短点,而让出现概率低的字符更长点,不就可以让整句话的编码缩短吗?
知道了原理,实现起来就简单了,给出我的代码:
#include<iostream>
#include<vector>
#include<string>
#include<stack>
using namespace std;
struct TreeNode {//树节点的构造
int val;
char ch;
struct TreeNode *left, *right;
TreeNode(int v, char c) :val(v), ch(c), left(NULL), right(NULL) {}
};
struct Node {//链节点的构造
TreeNode tree;//树节点
struct Node *next;
Node(int v,char c):tree(v,c),next(NULL) {}
};
Node* sort(Node *list,Node *item) {//链表排序
Node *p = list, *r;
if (p->tree.val > item->tree.val) {
item->next = p;
list = item;
}
else {
r = p; p = p->next;
while (p != NULL) {
if (p->tree.val > item->tree.val) {
r->next = item;
item->next = p;
break;
}
r = p; p = p->next;
}
r->next = item;
}
return list;
}
void code(TreeNode *t, string &cd) {//运用递归实现哈夫曼编码的生成
if (t->left != NULL || t->right != NULL) {
cd.push_back(‘0‘); code(t->left, cd);
cd.pop_back();
cd.push_back(‘1‘); code(t->right, cd);
cd.pop_back();
}
else
cout << t->ch << ‘ ‘ << cd << endl;
}
void getpower(string &str) {//获取权值并创建有序链表生成哈夫曼树
vector<int>recode(129, 0);//129位的数组记录每个字符的出现次数
Node *list = NULL, *p, *r=NULL;
for (int i = 0; i < int(str.length()); i++)
recode[str[i]]++;
int n = 0;
for (int i = 0; i < int(recode.size()); i++) {//对每一个链节点进行初始化
if (recode[i]){
if (list == NULL) {
list = (Node*)malloc(sizeof(Node));
list->tree.val = recode[i];
list->tree.ch = i;
list->tree.left = NULL;
list->tree.right = NULL;
list->next = NULL;
}
else {
p = (Node*)malloc(sizeof(Node(recode[i], i)));
p->tree.val = recode[i];
p->tree.ch = i;
p->tree.left = NULL;
p->tree.right = NULL;
p->next = NULL;
list = sort(list, p);//排序
}
n++;
}
}
p = list;
while (p != NULL) {//输出检验
cout << p->tree.ch << ":" << p->tree.val << endl;
p = p->next;
}
while (n != 1) {
p = list->next;
r = (Node*)malloc(sizeof(Node));
r->next = NULL;
r->tree.val = list->tree.val + p->tree.val;
r->tree.ch = 0;
r->tree.left = &list->tree;
r->tree.right = &p->tree;
list = p->next;
if(list!=NULL)
list = sort(list, r);
n--;
}
string s;
cout << "\n生成编码:\n";
code(&r->tree,s);
}
int main() {
string str="Create HaffmanCode!";
getpower(str);
return 0;
}
生成如下哈夫曼树:
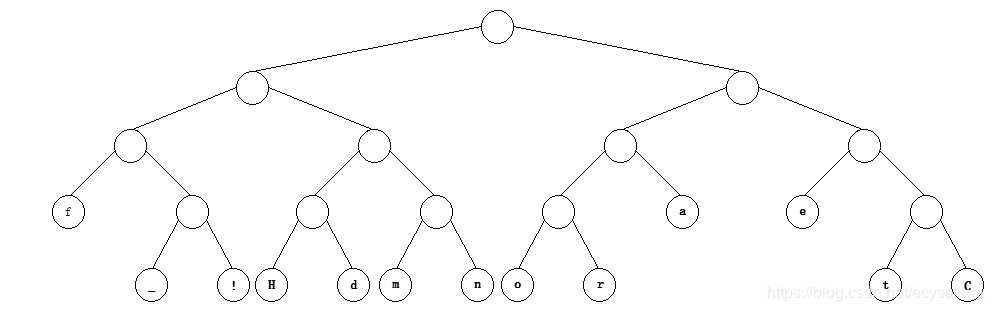
在这里我要说一下,一句话的哈夫曼编码是不唯一的,因为有的字符概率一样。而且有的哈夫曼编码的长度甚至还不一样,这就是另外一个问题了。
最后,聪明的小朋友可能还发现了哈夫曼编码的另一好处就是任何一个字符的编码都不会是其他字符的前缀,这就确保了即使传输的过程中没有空格,依然能够解码出相应的内容,这也是哈夫曼编码受到广泛应用的原因。
最后是个人设计过程中的总结:虽然代码看起来很多,但是只要思路清晰,而且用对了数据结构就很容易实现你想要的操作。以上代码是我在原来的基础上优化后的结果,本来还是想使用结构体的构造函数,还有在输出编码时使用迭代法实现。但都没有完成。等以后回头再看看。
标签:ret ddd 方式 存储空间 return iostream alt 技术 初始化
原文地址:https://www.cnblogs.com/1000sakura/p/10015542.html