标签:重复 div 过程 i++ 结果 swa min 桶排序 相对
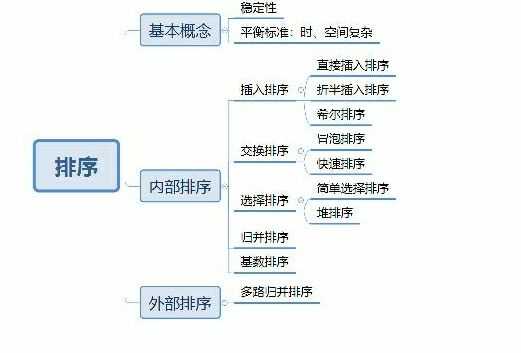
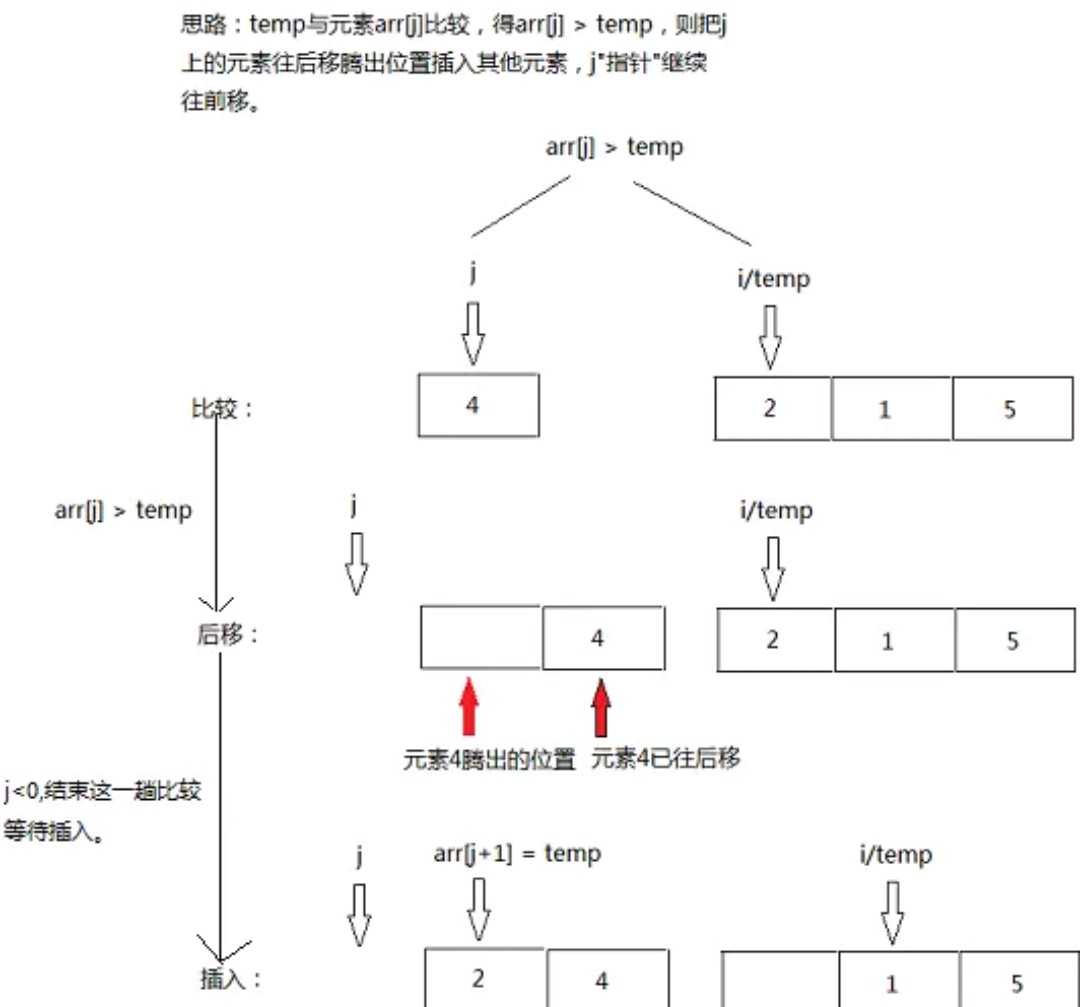
3.插入排序伪代码
1 void InsertSort (ElemType A[], int n) 2 { 3 int i,j; 4 for(i=2;i<=n;i++) 5 if(A[i].key<A[i-1].key) 6 { 7 A[0]=A[i]; 8 for(j=i-1;A[0].key<A[j].key;--j) 9 A[j+i]=A[j]; 10 A[j+i]=A[0]; 11 } 12 }
4.稳定性
由于每次插入元素时总是从后往前先比较在移动,所以不会出现相同元素相对位置,发生变化的情况即直接插入排序是一个稳定的排序方法
5.时间复杂度:O(n2)
?希尔排序(缩小增量排序)
1.算法提出:
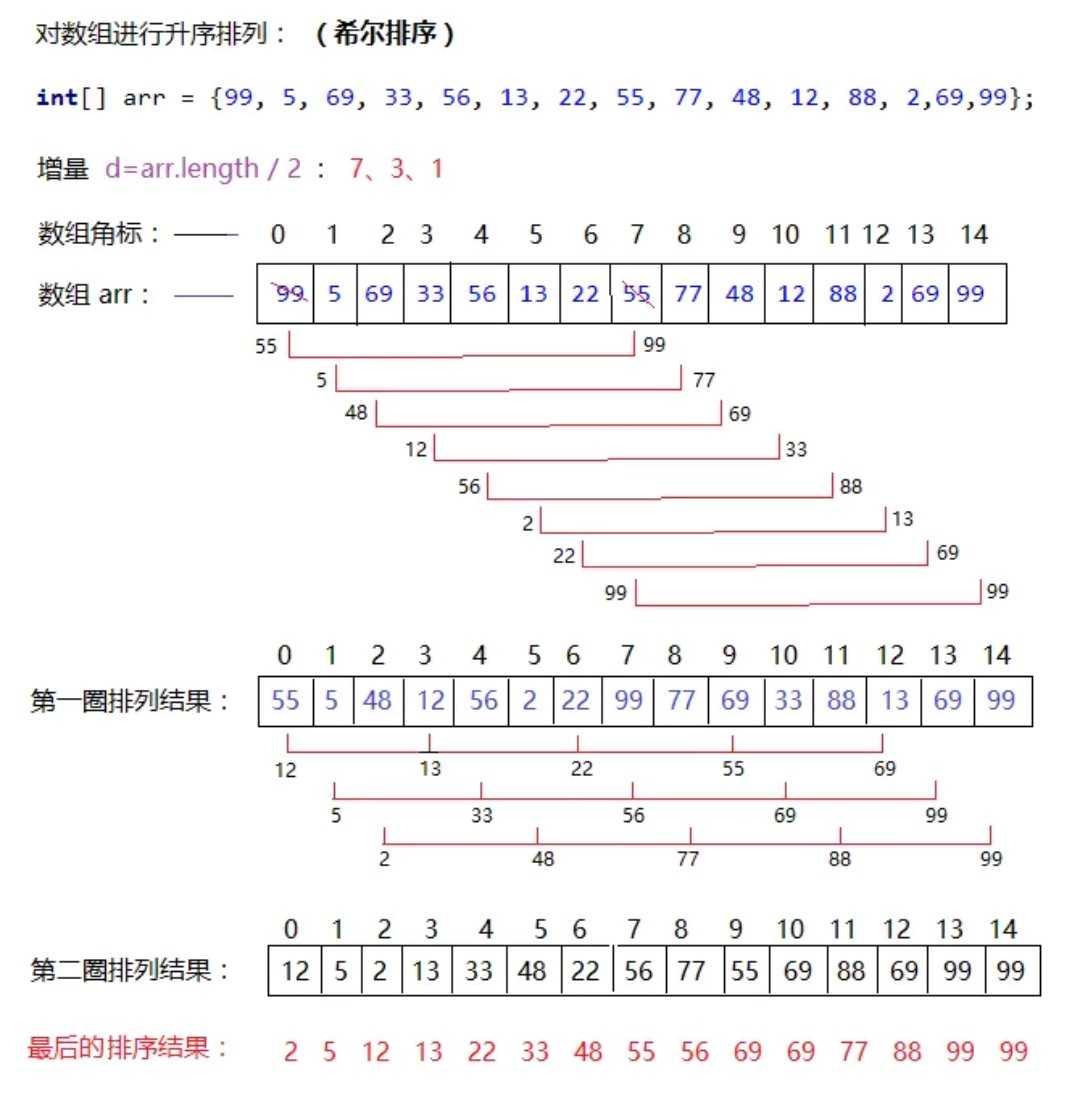
补充:操作原理时间复杂度与选取的增量序列有关且所取增量序列的函数介于O(N*logN)和O(n2)之间增量序列有很多种取法,但是使增量序列中的值没有除1之外的公因子,并且增量序列中最后一个值必须为1。
4.插入排序伪代码
1 void ShellSort (ElemType A[],int n){ 2 //对顺序表作希尔插入排序,基本算法和直接插入排序相比,做了以下修改: 3 //1.前后记录位置的增量是dk,不是1 4 //2.r[0]只是暂时存储单元,不是哨兵,当j<=0时,插入位置已到 5 for(dk=n/2;dk>=1,dk=dk/2) //步长变化 6 for(i=dk+1;i<=n;++i) 7 if(A[i].key<A[i-dk].key){ //需将A[i]插入有序增量子表 8 A[0]=A[i]; 9 for(j=i-dk;j>0&&A[0].key<A[j].key;j-=dk) 10 A[j+dk]=A[j]; //记录后移,查找插入位置 11 A[j+dk]=A[0]; //插入 12 }//if 13 }
5.稳定性
当相同关键字的记录被划分到不同的子表时,可能会改变它们之间的相对次序,因此,希尔排序是一种不稳定的排序方法。例如,表L=[3,2,2].经过一趟排序后,
L=[2,2,3],最终排序序列也是L=[2,2,3],显然2与2的相对次序已经发生了变化。
6.时间复杂度:O(N*logN)
?选择排序
1.算法思想
Step1:将待排序数组分为有序和无序两组(初始情况下有序组为空)
Step2:从左向右扫描无序组,找出最小的元素,将其放置在无序组的第一个位置。至此有序组++,无序组--;
Step3:重复Step2,直至无序组只剩下一个元素。
2.算法实现
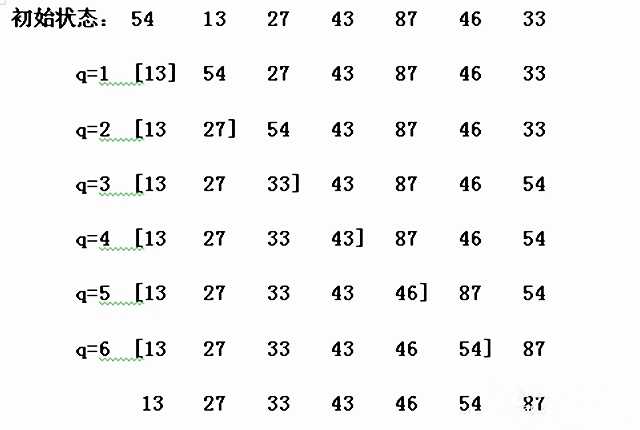
3.插入排序伪代码
1 void ShellSort (ElemType A[],int n){ 2 //对表A作简单的选择排序,A[]从0开始放元素 3 for(i=0;i<=n-1;i++){ //一共进行n-1趟 4 min=i; //记录最小元素位置 5 for(j=i+1;j<n;j++) //在A[i...n-1]中选择最小的元素 6 if(A[j]<A[min]) 7 min=j; //更新最小元素位置 8 if(min!=i) swap(A[i],A[min]); //在第n个元素交换 9 10 } 11 }
4.时间复杂度: O(n2)
5.稳定性:
选择排序的时间复杂度为O(n2),由于每次选择仅考虑某一位置上的数据情况,可能会破坏之前数据的相对位置,因此它是一种不稳定的排序方法。 例如:序列[9,9,1]第一次就将第一个[9]与[1]交换,导致第一个9挪动到第二个9后面。
补充:简单选择排序的比较次数与序列的初始排序无关。假设待排序的序列有 n个元素,选择排序的赋值操作介于0和3(n - 1) 次之间; 则比较次数 永远都是n (n- 1) / 2; 而移动次数(即:交换操作)与序列的初始排序有关,介于 0 和 (n - 1) 次之间。当序列正序时,移动次数最少,为 0。当序列反序时,移动次数最多,为n - 1 次;逆序交换n/2次。选择排序的移动次数比冒泡排序少多了,由于交换所需CPU时间比 比较所需的CPU时间多,n值较小时,选择排序比冒泡排序快。
后续未完...
标签:重复 div 过程 i++ 结果 swa min 桶排序 相对
原文地址:https://www.cnblogs.com/blancheiii/p/10029530.html