关联分析:用于发现隐藏在大型数据集中的有意义的联系
项集:0或多个项的集合。例如:{啤酒,尿布,牛奶,花生} 是一个4-项集,意义想象成爸爸去超市买啤酒和花生,给儿子和老婆分别买尿布和牛奶。
关联规则:啤酒->花生,其强度可用支持度和置信度来度量
支持度:一个项集或者规则在所有事物中出现的频率,即此规则能否普遍运用于给定数据集。σ(X):表示项集X的支持度计数,项集X的支持度:s(X)=σ(X)/N;规则X → Y的支持度:s(X → Y) = σ(X∪Y) / N
置信度:确定Y在包含X的事务中出现的频繁程度。c(X → Y) = σ(X∪Y)/σ(X)
支持度是用来判断规则有没有意义,删去无意义规则;置信度度量是通过规则进行推理具有可靠性。对于给定的规则X → Y,置信度越高,Y在包含X的事物中出现的可能性就越大。即Y在给定X下的条件概率P(Y|X)越大。
2.Groceries是arules包自带的超市经营一个月的购物数据,含9835次交易,9835次/30天/12小时/天=27.3笔/小时->此超市属于中型超市
2.1数据源
2.2探索和准备数据
1 inspect(Groceries[1:5]) #通过inspect函数查看Groceries数据集的前5次交易记录 2 itemFrequency(Groceries[,1:3]) #itemFrequency()函数可以查看商品的交易比例<br>frankfurter sausage liver loaf <br>0.058973055 0.093950178 0.005083884
3 summary(Groceries)

交易比例

总体情况


2.3可视化商品的支持度——商品的频率图
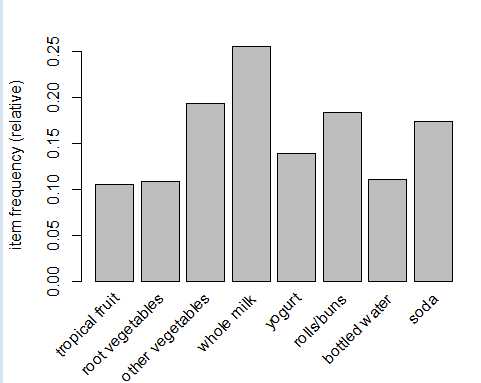
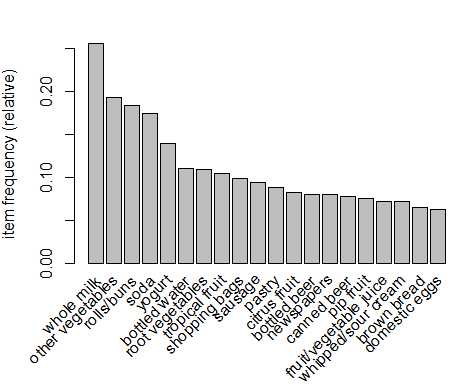
为了直观地呈现统计数据,可以使用itemFrequenctyPlot()函数生成一个用于描绘所包含的特定商品的交易比例的柱状图。因为包含很多种商品,不可能同时展现出来,因此可以通过support或者topN参数进行排除一部分商品进行展示
> itemFrequencyPlot(Groceries,support = 0.1) # support = 0.1 表示支持度至少为0.1 > itemFrequencyPlot(Groceries,topN = 20) # topN = 20 表示支持度排在前20的商品
2.4可视化交易数据,绘制稀疏矩阵
1 image(Groceries[1:5]) # 生成一个5行169列的矩阵,矩阵中填充有黑色的单元表示在此次交易(行)中,该商品(列)被购买了
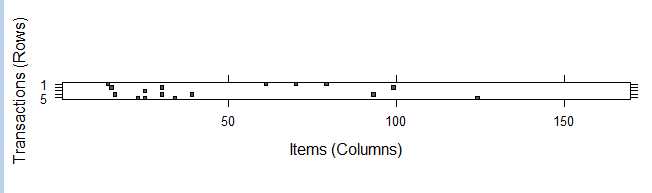
从上图可以看出,第一行记录(交易)包含了四种商品(黑色的方块),这种可视化的图是用于数据探索的一种很有用的工具。它可能有助于识别潜在的数据问题,比如:由于列表示的是商品名称,如果列从上往下一直被填充表明这个商品在每一次交易中都被购买了;另一方面,图中的模式可能有助于揭示交易或者商品的有趣部分,特别是当数据以有趣的方式排序后,比如,如果交易按照日期进行排序,那么黑色方块图案可能会揭示人们购买商品的数量或者类型受季节性的影响。这种可视化对于超大型的交易数据集是没有意义的,因为单元太小会很难发现有趣的模式。
2.5训练模型
1 grocery_rules <- apriori(data=Groceries,parameter=list(support =0.1,confidence =0.8,minlen =2))
support=0.1意味着商品至少出现在9835*0.1=983.5次交易中(所有买的人中必须有983.5个人购买),在前面的分析中,我们发现只有8种商品的 support >= 0.1,因此使用默认的设置没有产生任何规则也不足为奇。
minlen = 2 表示规则中至少包含两种商品,这可以防止仅仅是由于某种商品被频繁购买而创建的无用规则,比如在上面的分析中,我们发现whole milk出现的概率(支持度)为25.6%,很可能出现如下规则:{}=>whole milk,这种规则是没有意义的。
1 > grocery_rules=apriori(data=Groceries,parameter=list(support=0.006,confidence=0.25,minlen=2))#此时支持度取我们认为的最小交易数量9835*0.006=60次/月,置信度为25%,
即规则正确率至少为25%,排除了最不可靠的规则
结果如下,创建了463项规则

2.6评估性能
1 > summary(grocery_rules) 2 set of 463 rules 3 4 rule length distribution (lhs + rhs):sizes #前件+后件的规则分布 5 2 3 4 6 150 297 16 #有150个规则包含2件商品,297个规则包含3件商品,16个规则包含4件商品 7 8 Min. 1st Qu. Median Mean 3rd Qu. Max. 9 2.000 2.000 3.000 2.711 3.000 4.000 10 11 summary of quality measures: 12 support confidence lift count 13 Min. :0.006101 Min. :0.2500 Min. :0.9932 Min. : 60.0 14 1st Qu.:0.007117 1st Qu.:0.2971 1st Qu.:1.6229 1st Qu.: 70.0 15 Median :0.008744 Median :0.3554 Median :1.9332 Median : 86.0 16 Mean :0.011539 Mean :0.3786 Mean :2.0351 Mean :113.5 17 3rd Qu.:0.012303 3rd Qu.:0.4495 3rd Qu.:2.3565 3rd Qu.:121.0 18 Max. :0.074835 Max. :0.6600 Max. :3.9565 Max. :736.0 19 20 mining info: 21 data ntransactions support confidence 22 Groceries 9835 0.006 0.25
lift(提升度):相对于一般购买率,受前件影响之后,后件的购买率提升了多少,规则解读见如下:
1 > inspect(grocery_rules[1:5]) 2 lhs rhs support confidence lift count 3 [1] {pot plants} => {whole milk} 0.006914082 0.4000000 1.565460 68
4 [2] {pasta} => {whole milk} 0.006100661 0.4054054 1.586614 60 5 [3] {herbs} => {root vegetables} 0.007015760 0.4312500 3.956477 69 6 [4] {herbs} => {other vegetables} 0.007727504 0.4750000 2.454874 76 7 [5] {herbs} => {whole milk} 0.007727504 0.4750000 1.858983 76
第一条规则解读:
规则:{plot plants}->{whole milk}某顾客买了pot plants后还会购买whole milk; 支持度:该规则涵盖了0.7%的交易; 置信度:此规则发生的概率是40%; 提升度:相比于单买whole milk,买plot plants后再购买whole miik的可能性提升了1.565倍;1.56=40%的概率/25.6%的顾客,算出来一致
lift>1说明商品一起购买比单买更常见
2.7提高性能
标签:parameter 数据 summary 条件 推理 花生 1.5 pre nsa
原文地址:https://www.cnblogs.com/flowerfield423/p/10043177.html
