标签:人工 如何 告诉 learn 9.png margin 趋势 数据 计算公式
本文着重是重新梳理一下线性回归的概念,至于几行代码实现,那个不重要,概念明确了,代码自然水到渠成。
“机器学习”对于普通大众来说可能会比较陌生,但是“人工智能”这个词简直是太火了,即便是风云变化的股市中,只要是与人工智能、大数据、云计算相关的概念股票都会有很好的表现。机器学习是实现人工智能的基础,今天早上看了美国著名演员威尔斯密斯和世界最顶级的机器人进行对话的视频,视频中的机器人不论从语言还是表情都表达的非常到位,深感人工智能真的离我们越来越近了,所以学习人工智能前沿技术的基础学科——机器学习就非常有必要了。
首先,机器学习是一个比较容易理解的概念,就是让机器去模拟人的大脑去学习和思考,最终得出结论。举个栗子:某初中期末考试,有一道考题是给出直角坐标系中的两个点a(x1,y1),b(x2,y2),根据所给点求取过a,b两点的方程。初中文化的童鞋都知道,套用数学公式y=kx+b即可求出k和b就得到方程了。如何让计算机求出方程呢,这里就会涉及到非常简单的线性回归方法,也就是把已知的a,b点给计算机,然后告诉它用线性回归来拟合所给点,这时电脑也会给出你k和b的结果。也就是说电脑也会用老师告诉你的那套数学计算方法来求取方程,只不过是求取过程被编写成了计算机代码来执行。
上面这个小例子简单的介绍了一下线性回归方法机器学习是怎么来执行的,当然,在我们实际采用线性回归来进行机器学习时会更复杂一些,首先得需要掌握一些机器学习中线性回归的基本知识。首先了解一下机器学习的基础知识,机器学习通常涉及到两个重要的参数,包括特征和标签,如何对这两个名词进行理解呢?特征我们可以认为是输入机器学习模型中的自变量,标签就是机器学习模型的输出结果。类比上面的y=kx+b,x就是特征,y就是标签,仅此而已。
接下来我们需要认识一下在用python进行机器学习时候需要用到的包——sklearn包。这个包非常重要,里面有非常多的模型算法,简单点说你想要通过一堆特征得到一个模型时候你就直接调用这个包然后把特征丢进去好了,说的简单,其实在做的时候特费劲。。。但是基本过程就是这样。
下面需要了解相关性这个概念,相关性分析会在很多机器学习中遇到,也就是研究事物之间发生有没有关系,关系有多大这么个事情。相关性有三种:分别包括正线性相关、负线性相关、非线性相关。如下图所示:
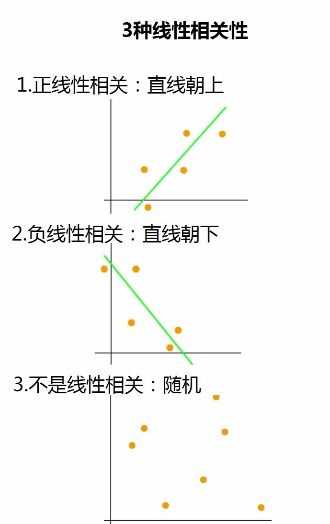
上图很直观看到了线性相关到底是咋回事,也就是说数据的趋势可以大致用一个直线来进行描述,虽然并不是所有的数据点都会在直线上,但是趋势就是直线。即趋势就是个最简单的方程y=kx+b。
说到相关性,最值得关注的有两个参数,1协方差,2相关系数。首先说协方差就是描述两个变量变化情况的量,如下示意图:
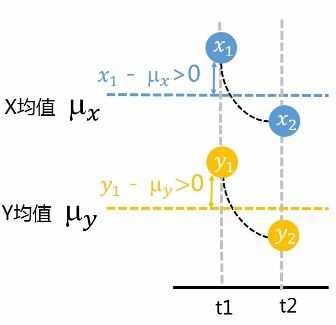
也就是你变大,我也变大,说明两个变量是同向变化,此时协方差为正;一个变量变大一个变量变小,说明两个变量是反向变化,协方差为负。从数值大小看,协方差数值越大,两个变量的同向程度也就越大,反之亦然。但是有的时候协方差会差上万倍,我们看到两个数的变化程度仍然相似,这时协方差就不适合来描述两个变量的相关性了。这时候我们需要用先关系数来描述两个数的相关性。计算公式如下图:
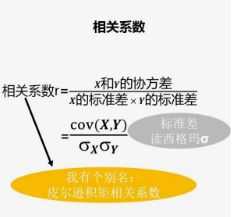
那么如何理解相关系数呢?首先标准差描述了变量在整体变化过程中偏离平均值的幅度。协方差除以标准差也就是把协方差中的变量变化幅度对协方差的影响剔除掉了,这样协方差也就标准化了,它反映的就是两个变量每单位变化的情况。
接下来就是逻辑回归的套路问题了,如下图:
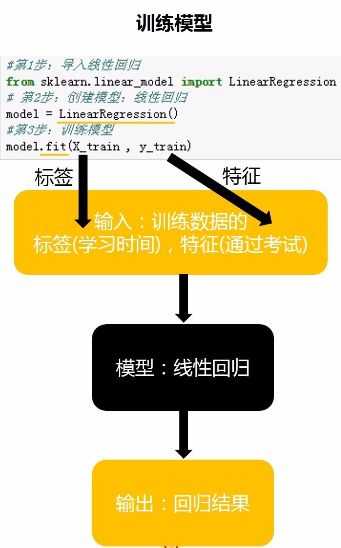
代码都很简单,但是功能很强大,通过上述这三行代码就可以像上文举的小栗子那样直接求出k和b了,然后直线方程就出来了。虽然模型出来了,但是并不是所有的数据点都是完全在模型中,这时我们需要评估这个模型到底咋样,靠不靠谱,就用如下公式来计算:
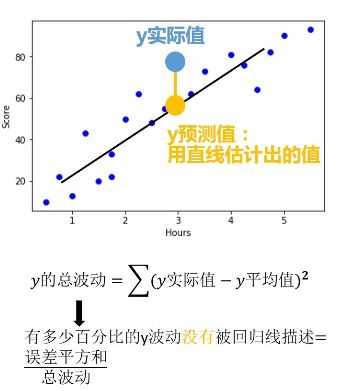
决定系数R平方有两个功能:1、回归线拟合程度2、r平方越高,回归模型越精确。
以上就是线性回归的基本知识,相信你只要有一点点基本的统计知识加上一点点高中数学知识最后再有点耐心就会明白线性回归的原理。
标签:人工 如何 告诉 learn 9.png margin 趋势 数据 计算公式
原文地址:https://www.cnblogs.com/zxyza/p/10050888.html