标签:head 研究 const flow 个数 == 结合 atm 技术分享
由于DeepFM算法有效的结合了因子分解机与神经网络在特征学习中的优点:同时提取到低阶组合特征与高阶组合特征,所以越来越被广泛使用。
在DeepFM中,FM算法负责对一阶特征以及由一阶特征两两组合而成的二阶特征进行特征的提取;DNN算法负责对由输入的一阶特征进行全连接等操作形成的高阶特征进行特征的提取。
具有以下特点:
DeepFM里关于“Field”和“Feature”的理解: 可参考我的文章FFM算法解析及Python实现中对Field和Feature的描述。
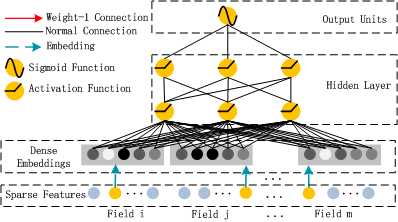
算法整体结构图如下所示:
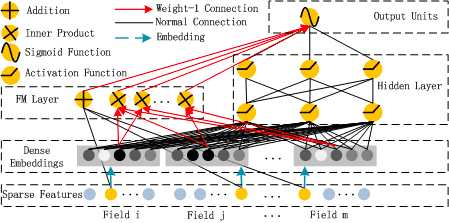
其中,DeepFM的输入可由连续型变量和类别型变量共同组成,且类别型变量需要进行One-Hot编码。而正由于One-Hot编码,导致了输入特征变得高维且稀疏。
应对的措施是:针对高维稀疏的输入特征,采用Word2Vec的词嵌入(WordEmbedding)思想,把高维稀疏的向量映射到相对低维且向量元素都不为零的空间向量中。
实际上,这个过程就是FM算法中交叉项计算的过程,具体可参考我的另一篇文章:FM算法解析及Python实现 中5.4小节的内容。
由上面网络结构图可以看到,DeepFM 包括 FM和 DNN两部分,所以模型最终的输出也由这两部分组成:
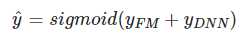
下面,把结构图进行拆分。首先是FM部分的结构:
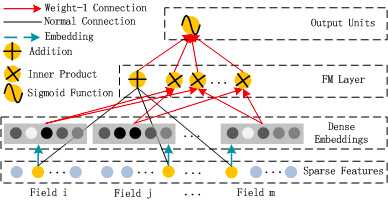
FM 部分的输出如下:
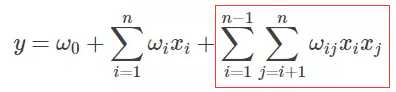
这里需要注意三点:
然后是DNN部分的结构:
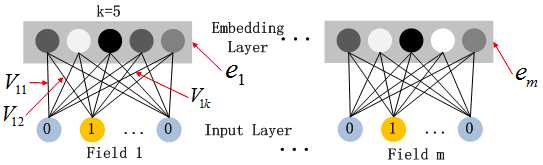
这里DNN的作用是构造高维特征,且有一个特点:DNN的输入也是embedding vector。所谓的权值共享指的就是这里。
关于DNN网络中的输入a处理方式采用前向传播,如下所示:
这里假设a(0)=(e1,e2,...em) 表示 embedding层的输出,那么a(0)作为下一层 DNN隐藏层的输入,其前馈过程如下。
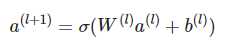
同样的,网上关于DeepFM算法实现有很多很多。需要注意的是两部分:一是训练集的构造,二是模型的设计。
主要是对连续型变量做正态分布等数据预处理操作、类别型变量的One-hot编码操作、统计One-hot编码后的特征数量、field_size的数量(注:原始特征数量)。
feature_value。对应的特征值,如果是离散特征的话,就是1,如果不是离散特征的话,就保留原来的特征值。
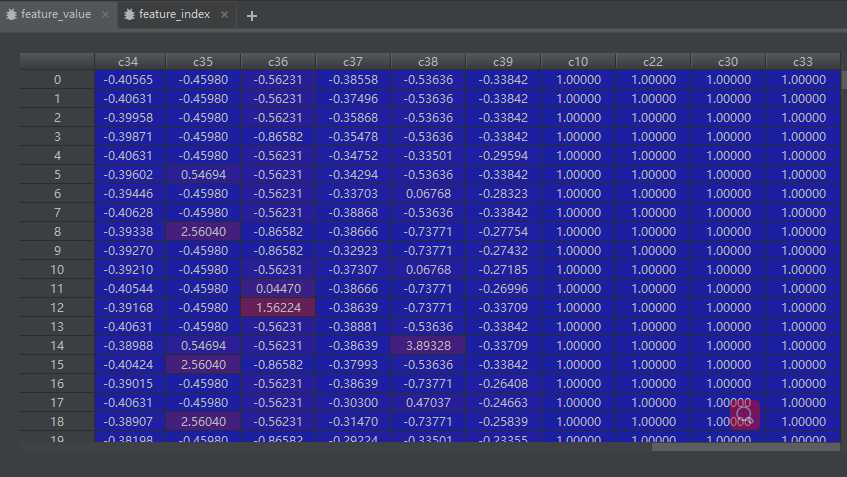
feature_index。用来记录One-hot编码后特征的序号,主要用于通过embedding_lookup选择我们的embedding。
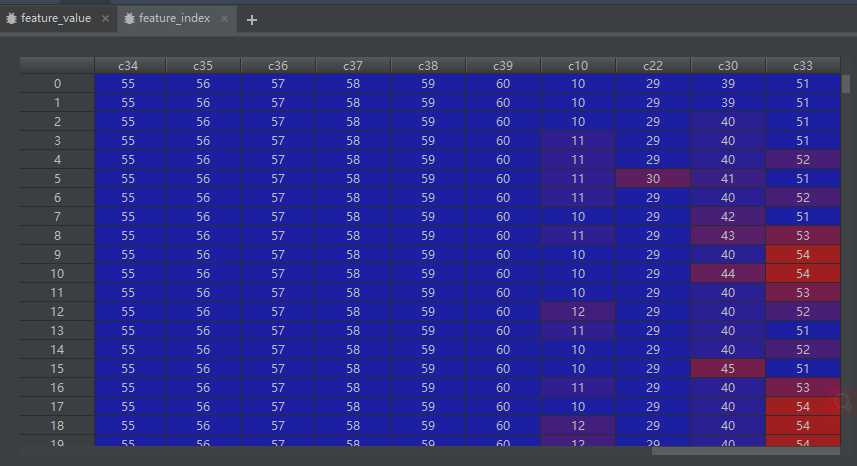
相关代码如下:
import pandas as pd def load_data(): train_data = {} file_path = ‘F:/Projects/deep_learning/DeepFM/data/tiny_train_input.csv‘ data = pd.read_csv(file_path, header=None) data.columns = [‘c‘ + str(i) for i in range(data.shape[1])] label = data.c0.values label = label.reshape(len(label), 1) train_data[‘y_train‘] = label co_feature = pd.DataFrame() ca_feature = pd.DataFrame() ca_col = [] co_col = [] feat_dict = {} cnt = 1 for i in range(1, data.shape[1]): target = data.iloc[:, i] col = target.name l = len(set(target)) # 列里面不同元素的数量 if l > 10: # 正态分布 target = (target - target.mean()) / target.std() co_feature = pd.concat([co_feature, target], axis=1) # 所有连续变量正态分布转换后的df feat_dict[col] = cnt # 列名映射为索引 cnt += 1 co_col.append(col) else: us = target.unique() print(us) feat_dict[col] = dict(zip(us, range(cnt, len(us) + cnt))) # 类别型变量里的类别映射为索引 ca_feature = pd.concat([ca_feature, target], axis=1) cnt += len(us) ca_col.append(col) feat_dim = cnt feature_value = pd.concat([co_feature, ca_feature], axis=1) feature_index = feature_value.copy() for i in feature_index.columns: if i in co_col: # 连续型变量 feature_index[i] = feat_dict[i] # 连续型变量元素转化为对应列的索引值 else: # 类别型变量 # print(feat_dict[i]) feature_index[i] = feature_index[i].map(feat_dict[i]) # 类别型变量元素转化为对应元素的索引值 feature_value[i] = 1. # feature_index是特征的一个序号,主要用于通过embedding_lookup选择我们的embedding train_data[‘xi‘] = feature_index.values.tolist() # feature_value是对应的特征值,如果是离散特征的话,就是1,如果不是离散特征的话,就保留原来的特征值。 train_data[‘xv‘] = feature_value.values.tolist() train_data[‘feat_dim‘] = feat_dim return train_data if __name__ == ‘__main__‘: load_data()
模型设计主要是完成了FM部分和DNN部分的结构设计,具体功能代码中都进行了注释。
import os import sys import numpy as np import tensorflow as tf from build_data import load_data BASE_PATH = os.path.dirname(os.path.dirname(__file__)) class Args(): feature_sizes = 100 field_size = 15 embedding_size = 256 deep_layers = [512, 256, 128] epoch = 3 batch_size = 64 # 1e-2 1e-3 1e-4 learning_rate = 1.0 # 防止过拟合 l2_reg_rate = 0.01 checkpoint_dir = os.path.join(BASE_PATH, ‘data/saver/ckpt‘) is_training = True class model(): def __init__(self, args): self.feature_sizes = args.feature_sizes self.field_size = args.field_size self.embedding_size = args.embedding_size self.deep_layers = args.deep_layers self.l2_reg_rate = args.l2_reg_rate self.epoch = args.epoch self.batch_size = args.batch_size self.learning_rate = args.learning_rate self.deep_activation = tf.nn.relu self.weight = dict() self.checkpoint_dir = args.checkpoint_dir self.build_model() def build_model(self): self.feat_index = tf.placeholder(tf.int32, shape=[None, None], name=‘feature_index‘) self.feat_value = tf.placeholder(tf.float32, shape=[None, None], name=‘feature_value‘) self.label = tf.placeholder(tf.float32, shape=[None, None], name=‘label‘) # One-hot编码后的输入层与Dense embeddings层的权值定义,即DNN的输入embedding。注:Dense embeddings层的神经元个数由field_size和决定 self.weight[‘feature_weight‘] = tf.Variable( tf.random_normal([self.feature_sizes, self.embedding_size], 0.0, 0.01), name=‘feature_weight‘) # FM部分中一次项的权值定义 # shape (61,1) self.weight[‘feature_first‘] = tf.Variable( tf.random_normal([self.feature_sizes, 1], 0.0, 1.0), name=‘feature_first‘) # deep网络部分的weight num_layer = len(self.deep_layers) # deep网络初始输入维度:input_size = 39x256 = 9984 (field_size(原始特征个数)*embedding个神经元) input_size = self.field_size * self.embedding_size init_method = np.sqrt(2.0 / (input_size + self.deep_layers[0])) # shape (9984,512) self.weight[‘layer_0‘] = tf.Variable( np.random.normal(loc=0, scale=init_method, size=(input_size, self.deep_layers[0])), dtype=np.float32 ) # shape(1, 512) self.weight[‘bias_0‘] = tf.Variable( np.random.normal(loc=0, scale=init_method, size=(1, self.deep_layers[0])), dtype=np.float32 ) # 生成deep network里面每层的weight 和 bias if num_layer != 1: for i in range(1, num_layer): init_method = np.sqrt(2.0 / (self.deep_layers[i - 1] + self.deep_layers[i])) # shape (512,256) (256,128) self.weight[‘layer_‘ + str(i)] = tf.Variable( np.random.normal(loc=0, scale=init_method, size=(self.deep_layers[i - 1], self.deep_layers[i])), dtype=np.float32) # shape (1,256) (1,128) self.weight[‘bias_‘ + str(i)] = tf.Variable( np.random.normal(loc=0, scale=init_method, size=(1, self.deep_layers[i])), dtype=np.float32) # deep部分output_size + 一次项output_size + 二次项output_size 423 last_layer_size = self.deep_layers[-1] + self.field_size + self.embedding_size init_method = np.sqrt(np.sqrt(2.0 / (last_layer_size + 1))) # 生成最后一层的结果 self.weight[‘last_layer‘] = tf.Variable( np.random.normal(loc=0, scale=init_method, size=(last_layer_size, 1)), dtype=np.float32) self.weight[‘last_bias‘] = tf.Variable(tf.constant(0.01), dtype=np.float32) # embedding_part # shape (?,?,256) self.embedding_index = tf.nn.embedding_lookup(self.weight[‘feature_weight‘], self.feat_index) # Batch*F*K # shape (?,39,256) self.embedding_part = tf.multiply(self.embedding_index, tf.reshape(self.feat_value, [-1, self.field_size, 1])) # [Batch*F*1] * [Batch*F*K] = [Batch*F*K],用到了broadcast的属性 print(‘embedding_part:‘, self.embedding_part) """ 网络传递结构 """ # FM部分 # 一阶特征 # shape (?,39,1) self.embedding_first = tf.nn.embedding_lookup(self.weight[‘feature_first‘], self.feat_index) # bacth*F*1 self.embedding_first = tf.multiply(self.embedding_first, tf.reshape(self.feat_value, [-1, self.field_size, 1])) # shape (?,39) self.first_order = tf.reduce_sum(self.embedding_first, 2) print(‘first_order:‘, self.first_order) # 二阶特征 self.sum_second_order = tf.reduce_sum(self.embedding_part, 1) self.sum_second_order_square = tf.square(self.sum_second_order) print(‘sum_square_second_order:‘, self.sum_second_order_square) self.square_second_order = tf.square(self.embedding_part) self.square_second_order_sum = tf.reduce_sum(self.square_second_order, 1) print(‘square_sum_second_order:‘, self.square_second_order_sum) # 1/2*((a+b)^2 - a^2 - b^2)=ab self.second_order = 0.5 * tf.subtract(self.sum_second_order_square, self.square_second_order_sum) # FM部分的输出(39+256) self.fm_part = tf.concat([self.first_order, self.second_order], axis=1) print(‘fm_part:‘, self.fm_part) # DNN部分 # shape (?,9984) self.deep_embedding = tf.reshape(self.embedding_part, [-1, self.field_size * self.embedding_size]) print(‘deep_embedding:‘, self.deep_embedding) # 全连接部分 for i in range(0, len(self.deep_layers)): self.deep_embedding = tf.add(tf.matmul(self.deep_embedding, self.weight["layer_%d" % i]), self.weight["bias_%d" % i]) self.deep_embedding = self.deep_activation(self.deep_embedding) # FM输出与DNN输出拼接 din_all = tf.concat([self.fm_part, self.deep_embedding], axis=1) self.out = tf.add(tf.matmul(din_all, self.weight[‘last_layer‘]), self.weight[‘last_bias‘]) print(‘output:‘, self.out) # loss部分 self.out = tf.nn.sigmoid(self.out) self.loss = -tf.reduce_mean( self.label * tf.log(self.out + 1e-24) + (1 - self.label) * tf.log(1 - self.out + 1e-24)) # 正则:sum(w^2)/2*l2_reg_rate # 这边只加了weight,有需要的可以加上bias部分 self.loss += tf.contrib.layers.l2_regularizer(self.l2_reg_rate)(self.weight["last_layer"]) for i in range(len(self.deep_layers)): self.loss += tf.contrib.layers.l2_regularizer(self.l2_reg_rate)(self.weight["layer_%d" % i]) self.global_step = tf.Variable(0, trainable=False) opt = tf.train.GradientDescentOptimizer(self.learning_rate) trainable_params = tf.trainable_variables() print(trainable_params) gradients = tf.gradients(self.loss, trainable_params) clip_gradients, _ = tf.clip_by_global_norm(gradients, 5) self.train_op = opt.apply_gradients( zip(clip_gradients, trainable_params), global_step=self.global_step) def train(self, sess, feat_index, feat_value, label): loss, _, step = sess.run([self.loss, self.train_op, self.global_step], feed_dict={ self.feat_index: feat_index, self.feat_value: feat_value, self.label: label }) return loss, step def predict(self, sess, feat_index, feat_value): result = sess.run([self.out], feed_dict={ self.feat_index: feat_index, self.feat_value: feat_value }) return result def save(self, sess, path): saver = tf.train.Saver() saver.save(sess, save_path=path) def restore(self, sess, path): saver = tf.train.Saver() saver.restore(sess, save_path=path) def get_batch(Xi, Xv, y, batch_size, index): start = index * batch_size end = (index + 1) * batch_size end = end if end < len(y) else len(y) return Xi[start:end], Xv[start:end], np.array(y[start:end]) if __name__ == ‘__main__‘: args = Args() data = load_data() args.feature_sizes = data[‘feat_dim‘] args.field_size = len(data[‘xi‘][0]) args.is_training = True with tf.Session() as sess: Model = model(args) # init variables sess.run(tf.global_variables_initializer()) sess.run(tf.local_variables_initializer()) cnt = int(len(data[‘y_train‘]) / args.batch_size) print(‘time all:%s‘ % cnt) sys.stdout.flush() if args.is_training: for i in range(args.epoch): print(‘epoch %s:‘ % i) for j in range(0, cnt): X_index, X_value, y = get_batch(data[‘xi‘], data[‘xv‘], data[‘y_train‘], args.batch_size, j) loss, step = Model.train(sess, X_index, X_value, y) if j % 100 == 0: print(‘the times of training is %d, and the loss is %s‘ % (j, loss)) Model.save(sess, args.checkpoint_dir) else: Model.restore(sess, args.checkpoint_dir) for j in range(0, cnt): X_index, X_value, y = get_batch(data[‘xi‘], data[‘xv‘], data[‘y_train‘], args.batch_size, j) result = Model.predict(sess, X_index, X_value) print(result)
最终计算结果如下:
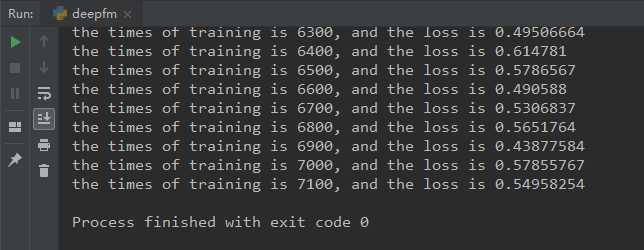
到此,关于CTR问题的三个算法(FM、FFM、DeepFM)已经介绍完毕,当然这仅仅是冰山一角,此外还有FNN、Wide&Deep等算法。感兴趣的同学可以自行研究。
此外,个人认为CTR问题的核心在于特征的构造,所以不同算法的差异主要体现在特征构造方面。
最后,附上一个CTR问题各模型的效果对比图。
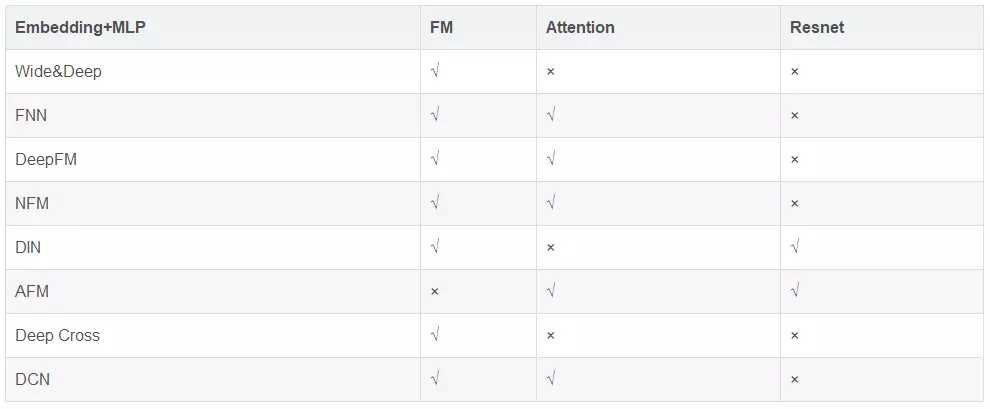
标签:head 研究 const flow 个数 == 结合 atm 技术分享
原文地址:https://www.cnblogs.com/wkang/p/9881921.html