标签:概率分布 over 期望 如何 和我 ima normal page com
本文是LDA主题模型的第二篇,读这一篇之前建议先读文本主题模型之LDA(一) LDA基础,同时由于使用了基于MCMC的Gibbs采样算法,如果你对MCMC和Gibbs采样不熟悉,建议阅读之前写的MCMC系列MCMC(四)Gibbs采样。
首先,回顾LDA的模型图如下:
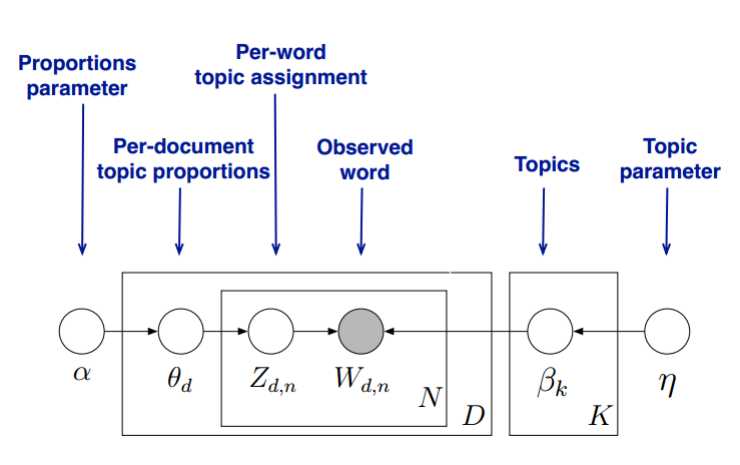
在Gibbs采样算法求解LDA的方法中,我们的α,ηα,η是已知的先验输入,我们的目标是得到各个zdn,wknzdn,wkn对应的整体z? ,w? z→,w→的概率分布,即文档主题的分布和主题词的分布。由于我们是采用Gibbs采样法,则对于要求的目标分布,我们需要得到对应分布各个特征维度的条件概率分布。
具体到我们的问题,我们的所有文档联合起来形成的词向量w? w→是已知的数据,不知道的是语料库主题z? z→的分布。假如我们可以先求出w,zw,z的联合分布p(w? ,z? )p(w→,z→),进而可以求出某一个词wiwi对应主题特征zizi的条件概率分布p(zi=k|w? ,z? ?i)p(zi=k|w→,z→?i)。其中,z? ?iz→?i代表去掉下标为ii的词后的主题分布。有了条件概率分布p(zi=k|w? ,z? ?i)p(zi=k|w→,z→?i),我们就可以进行Gibbs采样,最终在Gibbs采样收敛后得到第ii个词的主题。
如果我们通过采样得到了所有词的主题,那么通过统计所有词的主题计数,就可以得到各个主题的词分布。接着统计各个文档对应词的主题计数,就可以得到各个文档的主题分布。
以上就是Gibbs采样算法求解LDA的思路。
从上一节可以发现,要使用Gibbs采样求解LDA,关键是得到条件概率p(zi=k|w? ,z? ?i)p(zi=k|w→,z→?i)的表达式。那么这一节我们的目标就是求出这个表达式供Gibbs采样使用。
首先我们简化下Dirichlet分布的表达式,其中△(α)△(α)是归一化参数:
现在我们先计算下第d个文档的主题的条件分布p(z? d|α)p(z→d|α),在上一篇中我们讲到α→θd→z? dα→θd→z→d组成了Dirichlet-multi共轭,利用这组分布,计算p(z? d|α? )p(z→d|α→)如下: