标签:存在 牛顿法 情况 转化 false 就是 先来 如何 www.
本文是LDA主题模型的第三篇,读这一篇之前建议先读文本主题模型之LDA(一) LDA基础,同时由于使用了EM算法,如果你对EM算法不熟悉,建议先熟悉EM算法的主要思想。LDA的变分推断EM算法求解,应用于Spark MLlib和Scikit-learn的LDA算法实现,因此值得好好理解。
首先,回顾LDA的模型图如下:
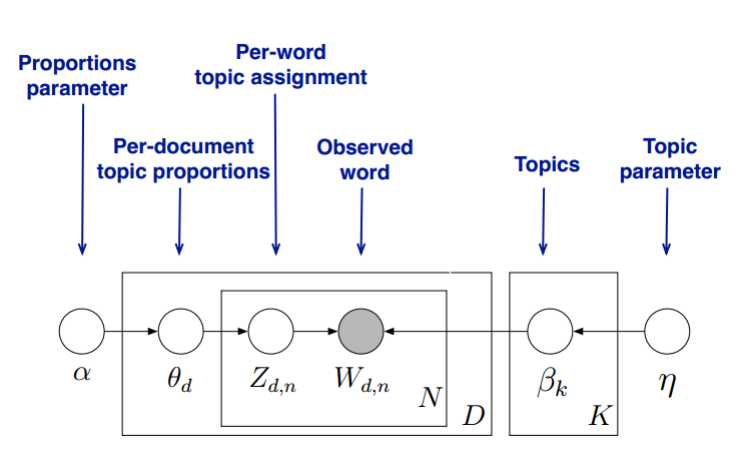
变分推断EM算法希望通过“变分推断(Variational Inference)”和EM算法来得到LDA模型的文档主题分布和主题词分布。首先来看EM算法在这里的使用,我们的模型里面有隐藏变量θ,β,zθ,β,z,模型的参数是α,ηα,η。为了求出模型参数和对应的隐藏变量分布,EM算法需要在E步先求出隐藏变量θ,β,zθ,β,z的基于条件概率分布的期望,接着在M步极大化这个期望,得到更新的后验模型参数α,ηα,η。
问题是在EM算法的E步,由于θ,β,zθ,β,z的耦合,我们难以求出隐藏变量θ,β,zθ,β,z的条件概率分布,也难以求出对应的期望,需要“变分推断“来帮忙,这里所谓的变分推断,也就是在隐藏变量存在耦合的情况下,我们通过变分假设,即假设所有的隐藏变量都是通过各自的独立分布形成的,这样就去掉了隐藏变量之间的耦合关系。我们用各个独立分布形成的变分分布来模拟近似隐藏变量的条件分布,这样就可以顺利的使用EM算法了。
当进行若干轮的E步和M步的迭代更新之后,我们可以得到合适的近似隐藏变量分布θ,β,zθ,β,z和模型后验参数α,ηα,η,进而就得到了我们需要的LDA文档主题分布和主题词分布。
可见要完全理解LDA的变分推断EM算法,需要搞清楚它在E步变分推断的过程和推断完毕后EM算法的过程。
要使用EM算法,我们需要求出隐藏变量的条件概率分布如下:
前面讲到由于θ,β,zθ,β,z之间的耦合,这个条件概率是没法直接求的,但是如果不求它就不能用EM算法了。怎么办呢,我们引入变分推断,具体是引入基于mean field assumption的变分推断,这个推断假设所有的隐藏变量都是通过各自的独立分布形成的,如下图所示:
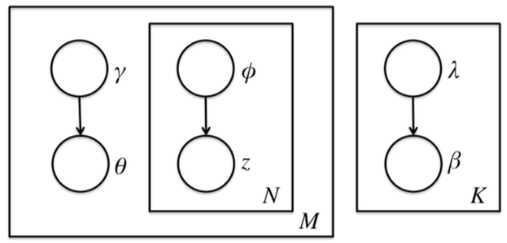
我们假设隐藏变量θθ是由独立分布γγ形成的,隐藏变量zz是由独立分布??形成的,隐藏变量ββ是由独立分布λλ形成的。这样我们得到了三个隐藏变量联合的变分分布qq为:
我们的目标是用q(β,z,θ|λ,?,γ)q(β,z,θ|λ,?,γ)来近似的估计p(θ,β,z|w,α,η)p(θ,β,z|w,α,η),也就是说需要这两个分布尽可能的相似,用数学语言来描述就是希望这两个概率分布之间有尽可能小的KL距离,即:
其中D(q||p)D(q||p)即为KL散度或KL距离,对应分布qq和pp的交叉熵。即:
我们的目的就是找到合适的λ?,??,γ?λ?,??,γ?,然后用q(β,z,θ|λ?,??,γ?)q(β,z,θ|λ?,??,γ?)来近似隐藏变量的条件分布p(θ,β,z|w,α,η)p(θ,β,z|w,α,η),进而使用EM算法迭代。
这个合适的λ?,??,γ?λ?,??,γ?,也不是那么好求的,怎么办呢?我们先看看我能文档数据的对数似然函数log(w|α,η)log(w|α,η)如下,为了简化表示,我们用Eq(x)Eq(x)代替Eq(β,z,θ|λ,?,γ)(x)Eq(β,z,θ|λ,?,γ)(x),用来表示xx对于变分分布q(β,z,θ|λ,?,γ)q(β,z,θ|λ,?,γ) 的期望。