simhash算法

标签：若是   抽屉原理   hashcode   img   转换   个数   blog   字符   cat   

1. SimHash与传统hash函数的区别

　　传统的Hash算法只负责将原始内容尽量均匀随机地映射为一个签名值，原理上仅相当于伪随机数产生算法。传统的hash算法产生的两个签名，如果原始内容在一定概率下是相等的；如果不相等，除了说明原始内容不相等外，不再提供任何信息，因为即使原始内容只相差一个字节，所产生的签名也很可能差别很大。所以传统的Hash是无法在签名的维度上来衡量原内容的相似度，而SimHash本身属于一种局部敏感哈希算法，它产生的hash签名在一定程度上可以表征原内容的相似度。

　　我们主要解决的是文本相似度计算，要比较的是两个文章是否相识，当然我们降维生成了hash签名也是用于这个目的。看到这里估计大家就明白了，我们使用的simhash就算把文章中的字符串变成 01 串也还是可以用于计算相似度的，而传统的hash却不行。我们可以来做个测试，两个相差只有一个字符的文本串，“你妈妈喊你回家吃饭哦，回家罗回家罗” 和 “你妈妈叫你回家吃饭啦，回家罗回家罗”。

　　通过simhash计算结果为：

　　1000010010101101111111100000101011010001001111100001001011001011

　　1000010010101101011111100000101011010001001111100001101010001011

　　通过传统hash计算为：

　　0001000001100110100111011011110

　　1010010001111111110010110011101

　　大家可以看得出来，相似的文本只有部分 01 串变化了，而普通的hash却不能做到，这个就是局部敏感哈希的魅力。

2. SimHash算法思想

　　假设我们有海量的文本数据，我们需要根据文本内容将它们进行去重。对于文本去重而言，目前有很多NLP相关的算法可以在很高精度上来解决，但是我们现在处理的是大数据维度上的文本去重，这就对算法的效率有着很高的要求。而局部敏感hash算法可以将原始的文本内容映射为数字（hash签名），而且较为相近的文本内容对应的hash签名也比较相近。SimHash算法是Google公司进行海量网页去重的高效算法，它通过将原始的文本映射为64位的二进制数字串，然后通过比较二进制数字串的差异进而来表示原始文本内容的差异。

3. SimHash流程实现

　　simhash是由 Charikar 在2002年提出来的，本文为了便于理解尽量不使用数学公式，分为这几步：

　　（注：具体的事例摘自Lanceyan的博客《海量数据相似度计算之simhash和海明距离》）

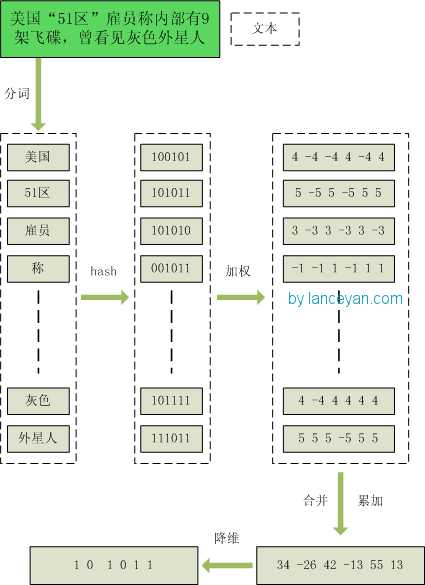
• 1、分词，把需要判断文本分词形成这个文章的特征单词。最后形成去掉噪音词的单词序列并为每个词加上权重，我们假设权重分为5个级别（1~5）。比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”，括号里是代表单词在整个句子里重要程度，数字越大越重要。

• 2、hash，通过hash算法把每个词变成hash值，比如“美国”通过hash算法计算为 100101,“51区”通过hash算法计算为 101011。这样我们的字符串就变成了一串串数字，还记得文章开头说过的吗，要把文章变为数字计算才能提高相似度计算性能，现在是降维过程进行时。

• 3、加权，通过 2步骤的hash生成结果，需要按照单词的权重形成加权数字串，比如“美国”的hash值为“100101”，通过加权计算为“4 -4 -4 4 -4 4”；“51区”的hash值为“101011”，通过加权计算为 “ 5 -5 5 -5 5 5”。

• 4、合并，把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。这里作为示例只算了两个单词的，真实计算需要把所有单词的序列串累加。

• 5、降维，把4步算出来的 “9 -9 1 -1 1 9” 变成 0 1 串，形成我们最终的simhash签名。 如果每一位大于0 记为 1，小于0 记为 0。最后算出结果为：“1 0 1 0 1 1”。

　　整个过程的流程图为：

4. SimHash签名距离计算

　　我们把库里的文本都转换为simhash签名，并转换为long类型存储，空间大大减少。现在我们虽然解决了空间，但是如何计算两个simhash的相似度呢？难道是比较两个simhash的01有多少个不同吗？对的，其实也就是这样，我们通过海明距离（Hamming distance）就可以计算出两个simhash到底相似不相似。两个simhash对应二进制（01串）取值不同的数量称为这两个simhash的海明距离。举例如下： 10101 和 00110 从第一位开始依次有第一位、第四、第五位不同，则海明距离为3。对于二进制字符串的a和b，海明距离为等于在a XOR b运算结果中1的个数（普遍算法）。

5. SimHash存储和索引

　　经过simhash映射以后，我们得到了每个文本内容对应的simhash签名，而且也确定了利用汉明距离来进行相似度的衡量。那剩下的工作就是两两计算我们得到的simhash签名的汉明距离了，这在理论上是完全没问题的，但是考虑到我们的数据是海量的这一特点，我们是否应该考虑使用一些更具效率的存储呢？其实SimHash算法输出的simhash签名可以为我们很好建立索引，从而大大减少索引的时间，那到底怎么实现呢？

　　这时候大家有没有想到hashmap呢，一种理论上具有O(1)复杂度的查找数据结构。我们要查找一个key值时，通过传入一个key就可以很快的返回一个value，这个号称查找速度最快的数据结构是如何实现的呢？看下hashmap的内部结构：

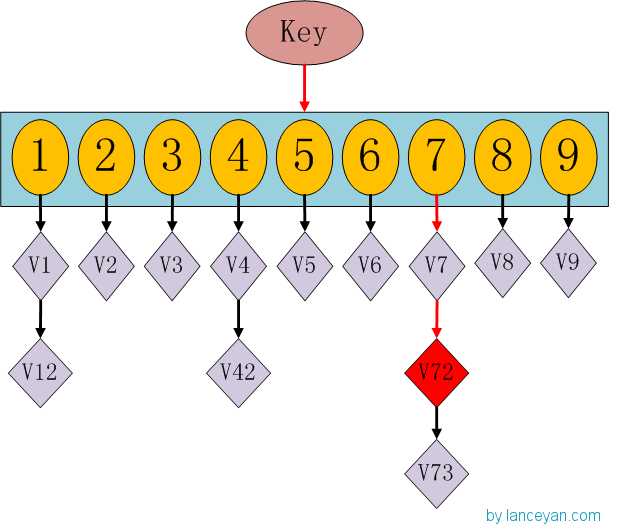
　　如果我们需要得到key对应的value，需要经过这些计算，传入key，计算key的hashcode，得到7的位置；发现7位置对应的value还有好几个，就通过链表查找，直到找到v72。其实通过这么分析，如果我们的hashcode设置的不够好，hashmap的效率也不见得高。借鉴这个算法，来设计我们的simhash查找。通过顺序查找肯定是不行的，能否像hashmap一样先通过键值对的方式减少顺序比较的次数。看下图：

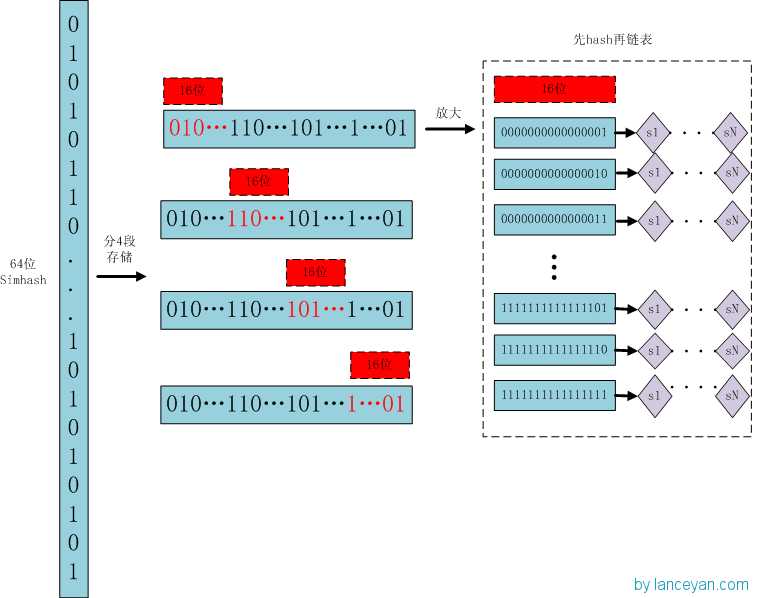
　　存储：
　　1、将一个64位的simhash签名拆分成4个16位的二进制码。（图上红色的16位）
　　2、分别拿着4个16位二进制码查找当前对应位置上是否有元素。（放大后的16位）
　　3、对应位置没有元素，直接追加到链表上；对应位置有则直接追加到链表尾端。（图上的 S1 — SN）

　　查找：
　　1、将需要比较的simhash签名拆分成4个16位的二进制码。
　　2、分别拿着4个16位二进制码每一个去查找simhash集合对应位置上是否有元素。
　　3、如果有元素，则把链表拿出来顺序查找比较，直到simhash小于一定大小的值，整个过程完成。

　　原理：
　　借鉴hashmap算法找出可以hash的key值，因为我们使用的simhash是局部敏感哈希，这个算法的特点是只要相似的字符串只有个别的位数是有差别变化。那这样我们可以推断两个相似的文本，至少有16位的simhash是一样的。具体选择16位、8位、4位，大家根据自己的数据测试选择，虽然比较的位数越小越精准，但是空间会变大。分为4个16位段的存储空间是单独simhash存储空间的4倍。之前算出5000w数据是 382 Mb，扩大4倍1.5G左右，还可以接受

6. SimHash存储和索引

　　1. 当文本内容较长时，使用SimHash准确率很高，SimHash处理短文本内容准确率往往不能得到保证；

　　2. 文本内容中每个term对应的权重如何确定要根据实际的项目需求，一般是可以使用IDF权重来进行计算。

7. 参考内容

　　1. 严澜的博客《海量数据相似度计算之simhash短文本查找》

　　2. 《Similarity estimation techniques from rounding algorithms》

作者：Poll的笔记 
博客出处：http://www.cnblogs.com/maybe2030/ 
本文版权归作者和博客园所有，欢迎转载，转载请标明出处。 

 方法介绍

背景

如果某一天，面试官问你如何设计一个比较两篇文章相似度的算法？可能你会回答几个比较传统点的思路：

• 一种方案是先将两篇文章分别进行分词，得到一系列特征向量，然后计算特征向量之间的距离（可以计算它们之间的欧氏距离、海明距离或者夹角余弦等等），从而通过距离的大小来判断两篇文章的相似度。
• 另外一种方案是传统hash，我们考虑为每一个web文档通过hash的方式生成一个指纹（finger print）。

下面，我们来分析下这两种方法。

• 采取第一种方法，若是只比较两篇文章的相似性还好，但如果是海量数据呢，有着数以百万甚至亿万的网页，要求你计算这些网页的相似度。你还会去计算任意两个网页之间的距离或夹角余弦么？想必你不会了。
• 而第二种方案中所说的传统加密方式md5，其设计的目的是为了让整个分布尽可能地均匀，但如果输入内容一旦出现哪怕轻微的变化，hash值就会发生很大的变化。

举个例子，我们假设有以下三段文本：

• the cat sat on the mat
• the cat sat on a mat
• we all scream for ice cream

使用传统hash可能会得到如下的结果：

• irb(main):006:0> p1 = ‘the cat sat on the mat‘
  • irb(main):007:0> p1.hash => 415542861
• irb(main):005:0> p2 = ‘the cat sat on a mat‘
  • irb(main):007:0> p2.hash => 668720516
• irb(main):007:0> p3 = ‘we all scream for ice cream‘
  • irb(main):007:0> p3.hash => 767429688 "

可理想当中的hash函数，需要对几乎相同的输入内容，产生相同或者相近的hash值，换言之，hash值的相似程度要能直接反映输入内容的相似程度，故md5等传统hash方法也无法满足我们的需求。

出世

车到山前必有路，来自于GoogleMoses Charikar发表的一篇论文“detecting near-duplicates for web crawling”中提出了simhash算法，专门用来解决亿万级别的网页的去重任务。

simhash作为locality sensitive hash（局部敏感哈希）的一种：

• 其主要思想是降维，将高维的特征向量映射成低维的特征向量，通过两个向量的Hamming Distance来确定文章是否重复或者高度近似。
  • 其中，Hamming Distance，又称汉明距离，在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。也就是说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：1011101 与 1001001 之间的汉明距离是 2。至于我们常说的字符串编辑距离则是一般形式的汉明距离。

如此，通过比较多个文档的simHash值的海明距离，可以获取它们的相似度。

流程

simhash算法分为5个步骤：分词、hash、加权、合并、降维，具体过程如下所述：

• 分词
  • 给定一段语句，进行分词，得到有效的特征向量，然后为每一个特征向量设置1-5等5个级别的权重（如果是给定一个文本，那么特征向量可以是文本中的词，其权重可以是这个词出现的次数）。例如给定一段语句：“CSDN博客结构之法算法之道的作者July”，分词后为：“CSDN 博客 结构 之 法 算法 之 道 的 作者 July”，然后为每个特征向量赋予权值：CSDN(4) 博客(5) 结构(3) 之(1) 法(2) 算法(3) 之(1) 道(2) 的(1) 作者(5) July(5)，其中括号里的数字代表这个单词在整条语句中的重要程度，数字越大代表越重要。
• hash
  • 通过hash函数计算各个特征向量的hash值，hash值为二进制数01组成的n-bit签名。比如“CSDN”的hash值Hash(CSDN)为100101，“博客”的hash值Hash(博客)为“101011”。就这样，字符串就变成了一系列数字。
• 加权
  • 在hash值的基础上，给所有特征向量进行加权，即W = Hash weight，且遇到1则hash值和权值正相乘，遇到0则hash值和权值负相乘。例如给“CSDN”的hash值“100101”加权得到：W(CSDN) = 1001014 = 4 -4 -4 4 -4 4，给“博客”的hash值“101011”加权得到：W(博客)=101011*5 = 5 -5 5 -5 5 5，其余特征向量类似此般操作。
• 合并
  • 将上述各个特征向量的加权结果累加，变成只有一个序列串。拿前两个特征向量举例，例如“CSDN”的“4 -4 -4 4 -4 4”和“博客”的“5 -5 5 -5 5 5”进行累加，得到“4+5 -4+-5 -4+5 4+-5 -4+5 4+5”，得到“9 -9 1 -1 1”。
• 降维
  • 对于n-bit签名的累加结果，如果大于0则置1，否则置0，从而得到该语句的simhash值，最后我们便可以根据不同语句simhash的海明距离来判断它们的相似度。例如把上面计算出来的“9 -9 1 -1 1 9”降维（某位大于0记为1，小于0记为0），得到的01串为：“1 0 1 0 1 1”，从而形成它们的simhash签名。

其流程如下图所示： 

应用

• 每篇文档得到SimHash签名值后，接着计算两个签名的海明距离即可。根据经验值，对64位的 SimHash值，海明距离在3以内的可认为相似度比较高。
  • 海明距离的求法：异或时，只有在两个比较的位不同时其结果是1 ，否则结果为0，两个二进制“异或”后得到1的个数即为海明距离的大小。

举个例子，上面我们计算到的“CSDN博客”的simhash签名值为“1 0 1 0 1 1”，假定我们计算出另外一个短语的签名值为“1 0 1 0 0 0”，那么根据异或规则，我们可以计算出这两个签名的海明距离为2，从而判定这两个短语的相似度是比较高的。

换言之，现在问题转换为：对于64位的SimHash值，我们只要找到海明距离在3以内的所有签名，即可找出所有相似的短语。

但关键是，如何将其扩展到海量数据呢？譬如如何在海量的样本库中查询与其海明距离在3以内的记录呢？

• 一种方案是查找待查询文本的64位simhash code的所有3位以内变化的组合
  • 大约需要四万多次的查询。
• 另一种方案是预生成库中所有样本simhash code的3位变化以内的组合
  • 大约需要占据4万多倍的原始空间。

这两种方案，要么时间复杂度高，要么空间复杂度复杂，能否有一种方案可以达到时空复杂度的绝佳平衡呢？答案是肯定的：

• 我们可以把 64 位的二进制simhash签名均分成4块，每块16位。根据鸽巢原理（也称抽屉原理），如果两个签名的海明距离在 3 以内，它们必有一块完全相同。如下图所示： 
• 然后把分成的4 块中的每一个块分别作为前16位来进行查找，建倒排索引。

具体如下图所示：

如此，如果样本库中存有2^34（差不多10亿）的simhash签名，则每个table返回2^(34-16)=262144个候选结果，大大减少了海明距离的计算成本。

• 假设数据是均匀分布，16位的数据，产生的像限为2^16个，则平均每个像限分布的文档数则为2^34/2^16 = 2^(34-16)) ，四个块返回的总结果数为 4* 262144 （大概 100 万）。
  • 这样，原本需要比较10亿次，经过索引后，大概只需要处理100万次。

（部分内容及图片参考自：http://grunt1223.iteye.com/blog/964564 ，后续图片会全部重画）

问题实例

待续。

@复旦李斌：simhash不是google发明的，是princeton的人早在stoc02上发表的。google在www07上的那篇论文只是在网页查重上应用了下。事实上www07中的算法是stoc02中随机超平面的一个极其巧妙的实现，bit差异的期望正好等于原姶向量的余弦。

simhash算法

标签：若是   抽屉原理   hashcode   img   转换   个数   blog   字符   cat   

原文地址：https://www.cnblogs.com/sddai/p/10088007.html