标签：bin   技术分享   ima   技术   2.4   2.3   相同   src   习惯   

Java数据结构和算法（一）树

前面讲到的链表、栈和队列都是一对一的线性结构，这节讲一对多的线性结构 - 树。「一对多」就是指一个元素只能有一个前驱，但可以有多个后继。

一、树

• 度(Degree) ：节点拥有的子树数。树的度是树中各个节点度的最大值。
• 节点 ：度为 0 的节点称为叶节点(Leaf)或终端节点。度不为 0 的节点称为分支节点。除根节点外，分支节点也被称为内部节点。
• 节点关系 ：节点的子树的根称为该节点的孩子(Child)。该结点称为孩子的双亲或父结点。同一个双亲的孩子之间互称为兄弟。
• 节点的层次 ：从根开始定义起，根为第一层，根的孩子为第二层。双亲在同一层的节点互为堂兄弟。树中节点的最大层次称为树的深度(Depth)或高度。
• 有序树 ：如果将树中节点的各个子树看成从左到右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。
• 森林 ：m(m>=0)棵互不相交的树的集合。

二、二叉树

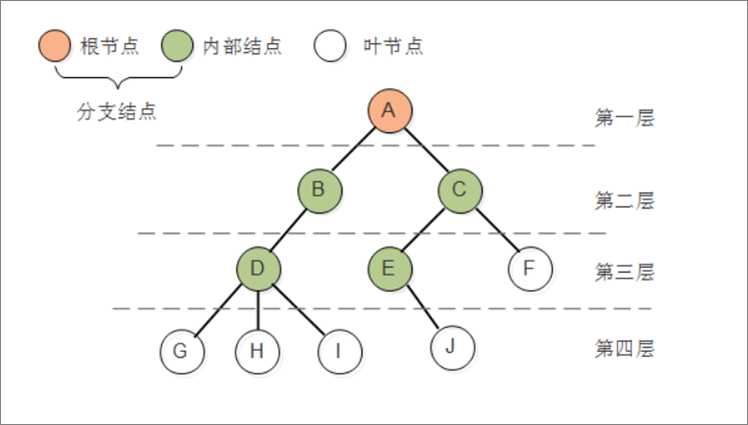
二叉树(Binary Tree)是树的特殊一种，具有如下特点：1、每个结点最多有两颗子树，结点的度最大为 2 ；2、左子树和右子树是有顺序的，次序不能颠倒；3、即使某结点只有一个子树，也要区分左右子树。

2.1 斜树

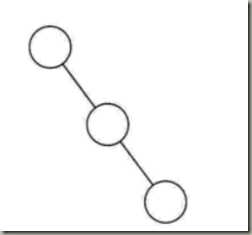
所有的结点都只有左子树（左斜树），或者只有右子树（右斜树）。这就是斜树，应用较少。

2.2 满二叉树

所有的分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样就是满二叉树。就是完美圆满的意思，关键在于树的平衡。

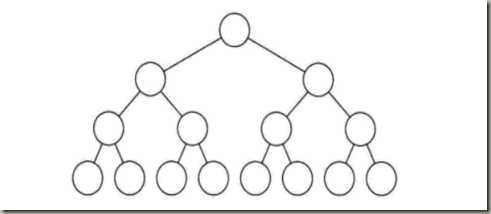
根据满二叉树的定义，得到其特点为：

1. 叶子只能出现在最下一层。
2. 非叶子结点度一定是 2。
3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

2.3 完全二叉树

对一棵具有 n 个结点的二叉树按层序排号，如果编号为 i 的结点与同样深度的满二叉树编号为 i 结点在二叉树中位置完全相同，就是完全二叉树。满二叉树必须是完全二叉树，反过来不一定成立。

其中关键点是按层序编号，然后对应查找。

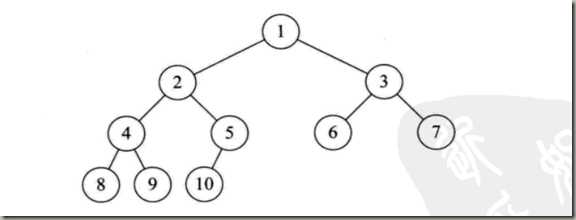
上图就是一个完全二叉树。

结合完全二叉树定义得到其特点：

1. 叶子结点只能出现在最下一层（满二叉树继承而来）
2. 最下层叶子结点一定集中在左 部连续位置。
3. 倒数第二层，如有叶子节点，一定出现在右部连续位置。
4. 同样结点树的二叉树，完全二叉树的深度最小（满二叉树也是对的）。

2.4 平衡二叉树

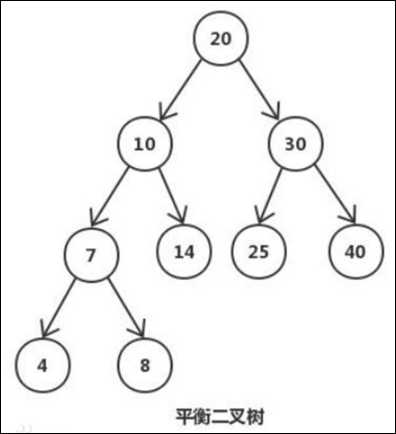
平衡二叉树又被称为 AVL 树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：

1. 它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树
2. 非叶子节值大于左边子节点、小于右边子节点；
3. 没有值相等重复的节点;

每天用心记录一点点。内容也许不重要，但习惯很重要！

Java数据结构和算法（一）树

标签：bin   技术分享   ima   技术   2.4   2.3   相同   src   习惯   

原文地址：https://www.cnblogs.com/binarylei/p/10090296.html