标签:nosql 时间 大小 OLE isl 性能 news etl let

计算机里面的数据结构 树 在计算机存储领域应用作用非常大,我之前也多次强调多磁盘的存取速度是目前计算机飞速发展的一大障碍,计算机革命性的的下一次飞跃就是看硬盘有没有质的飞跃,为什么这么说?因为磁盘是永久性存储设备(在相当长的时间内都可以用),就这一点虽然内存在性能方面优势巨大但是保存信息和数据还是要靠磁盘。
数最成功的要数B+tree和LSM-tree了,在关系型数据库和非关系型数据库(Nosql)可谓是处于主导地位,RocksDB目前在nosql和newsql中都大放光彩,其存储引擎就是LSM-tree,还有hbase,levelDB等。作为树的变种在存储领域不断突破性能的瓶颈。
/** * 二叉树的节点 * @author www.mojxtang.website * */ public class Node { /** * 关键字/索引(识别数据用) */ private int id; /** * 数据项(可以是任意对象T,也可以表示多个数据项) */ private int data; private Node leftChild; private Node rightChild; public Node(int id, int data) { super(); this.id = id; this.data = data; } public int getId() { return id; } public void setId(int id) { this.id = id; } public int getData() { return data; } public void setData(int data) { this.data = data; } public Node getLeftChild() { return leftChild; } public void setLeftChild(Node leftChild) { this.leftChild = leftChild; } public Node getRightChild() { return rightChild; } public void setRightChild(Node rightChild) { this.rightChild = rightChild; } @Override public String toString() { return "Node [id=" + id + ", data=" + data + ", leftChild=" + leftChild + ", rightChild=" + rightChild + "]"; } }
/** * 二叉搜索树操作(节点的左边小于节点值,而右边大于节点值) * @author www.mojxtang.website * */ public class BinaryTree { /** * 根节点 */ private Node root; /** * 查找一个节点 * @param key 关键字 ID值 * @return */ public Node find(int key) { Node current = root; while(current.getId() != key) { //如果key小于当前节点,就去找左边比当前小的节点 if (current.getId() > key) { current = current.getLeftChild(); //如果key大于当前节点,就去找右边比当前大的节点 }else if (current.getId() < key) { current = current.getRightChild(); } if (current == null) { return null; } } return current; } /** * 插入节点 * @param id * @param data */ public void insert(int id,int data) { Node newNode = new Node(id, data); if (root == null) { root = newNode; }else { //为什么这里要存放current=root和parent=null这两个节点对象? Node current = root; Node parent = null; while (true) { parent = current; //如果新节点小于当前节点,我们就去左子节点找 if (id < current.getId()) {//左边 current = current.getLeftChild(); //如果没有左子节点,说明我们找到了,可以将新节点插入到此 if (current == null) { parent.setLeftChild(newNode); return; } }else {//右边 current = current.getRightChild(); //如果没有右子节点,说明我们找到了,可以将新节点插入到此 if (current == null) { parent.setRightChild(newNode); return; } } } } } /** * 前序---获取节点数据 * @param node */ public void preOrder(Node node) { if (node !=null) { System.out.println(node.getId()+" - "); preOrder(node.getLeftChild()); preOrder(node.getRightChild()); } } /** * 中序--获取节点数据 * @param node */ public void inOrder(Node node) { if (node != null) { inOrder(node.getLeftChild()); System.out.println(node.getId()+" - "); inOrder(node.getRightChild()); } } /** * 后序--获取节点数据 * @param node */ public void aftOrder(Node node) { if (node != null) { aftOrder(node.getLeftChild()); aftOrder(node.getRightChild()); System.out.println(node.getId()+" - "); } } /** * 获取最小节点数据(使劲往左边找) * @param node */ public Node getMinNode() { Node current = root; Node minNode = null; while (current != null) { minNode = current; current = current.getLeftChild(); } return minNode; } /** * 获取最大节点数据(使劲往右边找) * @param node */ public Node getMaxNode() { Node current = root; Node maxNode = null; while (current != null) { maxNode = current; current = current.getRightChild(); } return maxNode; } /** * 删除一个节点(删除节点有两个子节点的时候,要用它的中序后继来代替该节点) * 算法是:找到被删除节点的右子节点,然后查找这个右子节点下的最后一个左子节点, * 也就是这颗子树的最小值节点,这就是被删除节点的中序后继节点。 * 三种情况: * 1.没有子节点 * 2.只有一个子节点 * 3.有两个子节点 * @param key * @return */ public boolean delete(int key) { //先找到需要删除的节点 Node current = root; Node parent = root; boolean isLeftNode = true; while (current.getId() != key) {//没有找到 parent = current; if (current.getId() > key) {//当前节点大于key,往左找 isLeftNode = true; current = current.getLeftChild(); }else if (current.getId() < key) {//当前节点小于key,往右找 isLeftNode = false; current = current.getRightChild(); } if (current == null) { return false; } } //1.没有子节点 if (current.getLeftChild() == null && current.getRightChild() == null) { this.noChild(parent, current, isLeftNode); } //2.只有一个节点 else if (current.getRightChild() == null) { this.oneLeftNode(parent, current, isLeftNode); } else if (current.getLeftChild() == null) { this.oneRightNode(parent, current, isLeftNode); } //3.有两个子节点 else { //找到中序后继节点 Node successor = this.getSuccessor(current); if (current == root) { root = successor; }else { if (isLeftNode) { parent.setLeftChild(successor); }else { parent.setRightChild(successor); } } //设置后继节点的左节点 successor.setLeftChild(current.getLeftChild()); } return true; } /** * 找到要删除节点的中序后继节点 * 算法是:找到被删除节点的右子节点,然后查找这个右子节点下的最后一个左子节点, * 也就是这颗子树的最小值节点,这就是被删除节点的中序后继节点。 * @param current * @return */ private Node getSuccessor(Node delNode) { //这里为什么记录三个节点对象? Node successor = delNode; Node successorParent = delNode; Node current = delNode.getRightChild(); //查找最后一个左子节点 while (current != null) { successorParent = successor; successor = current; current = current.getLeftChild(); } if (successor != delNode.getLeftChild()) { successorParent.setLeftChild(successor.getRightChild()); successor.setRightChild(delNode.getRightChild()); } return successor; } private void oneRightNode(Node parent,Node current,boolean isLeftNode) { if (current == root) { root = current.getRightChild(); }else { if (isLeftNode) { parent.setLeftChild(current.getRightChild()); }else { parent.setRightChild(current.getRightChild()); } } } private void oneLeftNode(Node parent,Node current,boolean isLeftNode) { if (current == root) { root = current.getLeftChild(); }else { //这里为什么设置父节点的左右都设置为current的左节点? if (isLeftNode) { parent.setLeftChild(current.getLeftChild()); }else { parent.setRightChild(current.getLeftChild()); } } } /** * 没有子节点 * @param parent * @param current * @param isLeftNode */ private void noChild(Node parent,Node current,boolean isLeftNode) { //如果是根节点 if (current == root) { root = null; }else { //这里为什么把父节点的左右值空? if (isLeftNode) { parent.setLeftChild(null); }else { parent.setRightChild(null); } } } public static void main(String[] args) { BinaryTree tree = new BinaryTree(); tree.insert(6, 212); tree.insert(5, 211); tree.insert(8, 221); tree.insert(3, 321); tree.insert(7, 421); tree.insert(9, 521); System.out.println(tree.root.toString()); tree.inOrder(tree.find(6)); System.out.println(tree.getMinNode()); System.out.println(tree.getMaxNode()); tree.delete(5); System.out.println(tree.root.toString()); } }
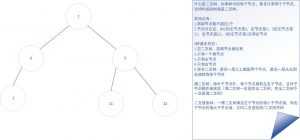
二叉搜索树是所有树结构的开始模型,它最明显的特性就是节点的左子节点比该节点大,比该节点的右子节点小,形成的树大家可以想想,我们可以说他“有序”。
大家不妨思考为什么在计算机里面会用这样的数据结构来做索引其实二叉树是没有节点的左右大小之分的,那为什么我们非要把左右节点搞出来个大小呢???
二叉搜索树复杂的就是删除大家看完代码会发现,数据的删除其实就是替换和制空的过程,这个过程有个关键性的操作就是存放临时变量,我在代码块里面备注的几个为什么大家思考思考是不是这个道理。
文章地址:java二叉搜索树原理
标签:nosql 时间 大小 OLE isl 性能 news etl let
原文地址:https://www.cnblogs.com/mojxtang/p/10122587.html