标签:vdc 图片 lcm tput 不可 LLC 分析 text 变化
base64编码原理:维基百科 - Base64
其实编码规则很简单,将字符串按每三个字符组成一组,因为每个字符的 ascii 码对应 0~127 之间(显然,不考虑其他字符集编码),即每个字符的二进制以 8 bit 存储,$ 3 \times 8 = 4 \times 6 $,这样就可以很方便的转为 4 个 6 bit 的字符,当一组中的字符(最后一组会出现这样的情况)少于3个字符,则用"="字符填充。
解码也就是一个逆过程,也不难。
既然是二进制,显然应该想到利用位操作。。。
注意到:
1. 6 bit 的二进制组成的数的十进制一定小于 64,$ (111111)_{2} = (63)_{10} $。这就是那张 base64 表的原因。
2.将前一个字符的多余的二进制,填充到后一位字符的二进制的前面以填充满 6 位,每 3 个字符为 1 周期 。
如果对位操作很熟练,那么这个算法会很简单(核心部分):
unsigned bit[6] = {0u};
size_t ens = 0, i = 2u;
for (unsigned j = 0u; inputs[j]; j++)
{
int asc_ = int(inputs[j]);
unsigned inx = asc_ >> i;
for (unsigned k = 0u; k < i - 2; k++)
inx += (bit[k] & 1) << (8 + k - i); // min: 0, max:{1, 2, 4, 8, 16, 32}
encode[ens++] = base64_table[inx];
if (i != 6) {
for (unsigned k = 0u, n = asc_; k < i; n >>= 1, k++)
bit[k] = n & 1;
i += 2;
}
else {
i = asc_;
inx = i >= 64 ? (i >= 128 ? i - 128 : i - 64) : i;
encode[ens++] = base64_table[inx];
if (inputs[j + 1] != ‘\0‘) i = 2;
}
}
下面从分析时间复杂度方向来解释算法:
unsigned bit[6] = {0u};
size_t ens = 0, i = 2u;
首先我们需要维护一个大小为6的无符号整形数组 bit 来存储6个二进制数位;
ens 是用来维护 encode 字符数组的栈下标;
变量 i 扮演了几个小而十分重要的角色:判断周期变化,维护扫描到的每一个字符当前应该做多少次的位移数,当 $ i = 6 $ ,意味着可以通过当前分组中的第3个字符的后 6 bit 编码得到第 4 个字符,这里为了减少局部变量冗余以及便利,我使用了 i 来多做了一点本不属于它的任务。
然后进入循环主体
for (unsigned j = 0u; inputs[j]; j++)
循环次数为我们需要编码的字符串的长度。
int asc_ = int(inputs[j]);
unsigned inx = asc_ >> i;
for (unsigned k = 0u; k < i - 2; k++)
inx += (bit[k] & 1) << (8 + k - i); // min: 0, max:{1, 2, 4, 8, 16, 32}
encode[ens++] = base64_table[inx];
上面代码片段的主要作用是:
1.将字符转为十进制ascii码
2.将 asc_ 右移 i 得到 6 bit,因为这里不用手动计算二进制,它本身就得到了一个 0~63 的十进制数,将其作为 base64 表的下标索引得到第一个字符(i 的所有取值情况为 { 2, 4, 6 } ,这也是 bit 数组为 6 的原因)。
3.如果程序进行到当前分组的第一个字符,那么循环
for (unsigned k = 0u; k < i - 2; k++)
inx += (bit[k] & 1) << (8 + k - i);
将不会进行,否则,计算该分组前一个字符存储在 bit 中的对应的 i 位上的值(计算字符移除的 bit 代码在后面,因为每组的第一个字符不需要计算加上 bit 的结果)。时间复杂度 $ O(1) $
例如(该例来自wikipedia - Base64):
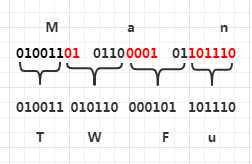
第一个字符右移出的2个bit(01)保存到bit数组,剩余的编码为 T 字符,扫描到字符 a 时,先将其值大小右移 4 位,变为 6(0110),将 bit 中的 2 个 bit 加到 0110 前面,也就是 010110,这里 bit 中的 1 的位为 4($ 1 \times 2^4 = 16 $ ),0的位为 5($ 0 \times 2^5 = 0 $ ), 可以根据 8 + k - i 来计算应该位移多少(注释中列举了可能情况)。
4.利用计算出的结果作为 base64 表的索引,取出对应的字符,并存储到 encode 栈中。
下一个片段:
if (i != 6) {
for (unsigned k = 0u, n = asc_; k < i; n >>= 1, k++)
bit[k] = n & 1;
i += 2;
}
当程序还在周期中进行时,程序就会进入到该片段,目的就是将当前字符后 i 个 bit 存储到 bit 数组中,以维护并填充下一个字符的前 i 个 bit。
否则执行片段:
else {
i = asc_;
inx = i >= 64 ? (i >= 128 ? i - 128 : i - 64) : i;
encode[ens++] = base64_table[inx];
if (inputs[j + 1] != ‘\0‘) i = 2;
}
当扫描到分组中第 3 个字符时,一个周期就结束了,因为 $ 4 \times 6 = 3 \times 8 $,所以,最后一个字符不需要位移,更准确的说,最后一个字符可以编码成两个字符,前 2 bit 结合前一个字符的后 4 bit,得到一个字符;后 6 bit 可以直接编码为一个字符。但如何将 8 bit 的前 2 个 bit 去掉呢?思考了一下,第7位二进制有效的最小的十进制值为64,第8位二进制有效的最小的十进制值为128,所以,就有了上面代码片段中第3行的代码,实际上,我们的输入是 ascii 字符集,不可能有大于等于 128 的情况,所以,可以写成:
inx = i >= 64 ? i - 64 : i;
然后将 inx 作为 base64 表的索引,取出字符并加入到 encode 栈顶。注意:inx 值是合法的,且一定不会导致越界发生。
最后如果下一个字符不是结束符,则将 i 重新置为 2,以开始新一轮的编码。当下一个字符为结束符时,i 的值一定大于 6(对于字母和数字的字符部分)。
核心部分基本就是这些了,但还有一些细节没处理。
对于上面的程序,当输入的字符串长度不能整除 3 时,最后一个字符的后面一部分一定会没有被编码出来,以及没有填充 "=" 来完成 base64 的编码规则。
所以,继续完善细节,见下面片段:
if (i <= 6)
{
unsigned inx = 0;
for (unsigned k = 0u; k < i - 2; k++)
inx += (bit[k] & 1) << (8 + k - i);
encode[ens++] = base64_table[inx];
}
while (i <= 6) encode[ens++] = ‘=‘, i += 2;
前面的程序的结束情况一定在 if 之后就完成循环了,最后一个字符的 8 bit 后面 i 部分存入 bit 中的后,没有用上,于是,将其取出来后面全填充为 0 并计算出值即可,然后判断循环结束前执行到周期的第几个字符(一定是1或2),填充上"="。时间复杂度 $ O(1) $
于是,该算法的总时间复杂度为 $ O(n) $ ,n 为字符串长度。
最后
完整实现代码:
#include <iostream>
#include <cstdio>
#include <cstring>
const char *base64_table = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
char* base64encode(char* encode, const char* inputs)
{
unsigned bit[6] = {0u};
size_t ens = 0, i = 2u;
for (unsigned j = 0u; inputs[j]; j++)
{
int asc_ = int(inputs[j]);
unsigned inx = asc_ >> i;
for (unsigned k = 0u; k < i - 2; k++)
inx += (bit[k] & 1) << (8 + k - i); // min: 0, max:{1, 2, 4, 8, 16, 32}
encode[ens++] = base64_table[inx];
if (i != 6) {
for (unsigned k = 0u, n = asc_; k < i; n >>= 1, k++)
bit[k] = n & 1;
i += 2;
}
else {
i = asc_;
inx = i >= 64 ? i - 64 : i;
encode[ens++] = base64_table[inx];
if (inputs[j + 1] != ‘\0‘) i = 2;
}
}
if (i <= 6)
{
unsigned inx = 0;
for (unsigned k = 0u; k < i - 2; k++)
inx += (bit[k] & 1) << (8 + k - i);
encode[ens++] = base64_table[inx];
}
while (i <= 6) encode[ens++] = ‘=‘, i += 2;
encode[ens] = 0;
return encode;
}
char* base64encode(char* encode, std::string inputs)
{
return base64encode(encode, inputs.c_str());
}
int main(int argc, char* argv[])
{
if (argc <= 1)
{
std::cout << "usage -i <input text>" << std::endl;
return 0;
}
if ( !strcmp(argv[1], "-i") )
{
std::string doc = argv[2];
int len = doc.size();
char* encode = new char[len * (4 / 3)];
std::cout << base64encode(encode, argv[2]) << std::endl;
delete[] encode;
encode = nullptr;
}
return 0;
}
测试一下(来自wiki - Base64):
base64encode -i "Man is distinguished, not only by his reason, but by this singular passion from other animals, which is a lust of the mind, that by a perseverance of delight in the continued and indefatigable generation of knowledge, exceeds the short vehemence of any carnal pleasure."
Output:
TWFuIGlzIGRpc3Rpbmd1aXNoZWQsIG5vdCBvbmx5IGJ5IGhpcyByZWFzb24sIGJ1dCBieSB0aGlzIHNpbmd1bGFyIHBhc3Npb24gZnJvbSBvdGhlciBhbmltYWxzLCB3aGljaCBpcyBhIGx1c3Qgb2YgdGhlIG1pbmQsIHRoYXQgYnkgYSBwZXJzZXZlcmFuY2Ugb2YgZGVsaWdodCBpbiB0aGUgY29udGludWVkIGFuZCBpbmRlZmF0aWdhYmxlIGdlbmVyYXRpb24gb2Yga25vd2xlZGdlLCBleGNlZWRzIHRoZSBzaG9ydCB2ZWhlbWVuY2Ugb2YgYW55IGNhcm5hbCBwbGVhc3VyZS4=
标签:vdc 图片 lcm tput 不可 LLC 分析 text 变化
原文地址:https://www.cnblogs.com/darkchii/p/10122404.html