标签:not python returns init 公式 技术 min mini sum
隔了好久木有更新了,因为发现自己numpy的很多操作都忘记了,加上最近有点忙.。。
接着上次
我们得到的迭代函数为
首先j != yi
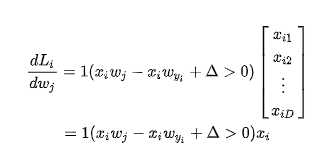
j = yi
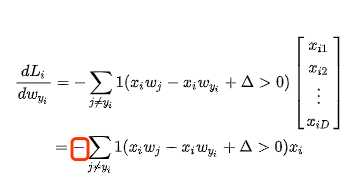
import numpy as np
def svm_loss_naive(W, X, y, reg):
"""
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in xrange(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in xrange(num_classes):
if j == y[i]: #根据公式,正确的那个不用算
continue
# 叠加margin
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
loss += margin
dW[:, y[i]] += -X[i, :] # 根据公式:?Wyi Li = - xiT(∑j≠yi1(xiWj - xiWyi +1>0)) + 2λWyi
dW[:, j] += X[i, :] # 根据公式: ?Wj Li = xiT 1(xiWj - xiWyi +1>0) + 2λWj , (j≠yi)
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += 0.5 * reg * np.sum(W * W)
dW += reg * W
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.Inputs and outputs
are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
scores = X.dot(W) # N by C
num_train = X.shape[0]
num_classes = W.shape[1]
scores_correct = scores[np.arange(num_train), y] # 1 by N
scores_correct = np.reshape(scores_correct, (num_train, 1)) # N by 1
margins = scores - scores_correct + 1.0 # N by C
margins[np.arange(num_train), y] = 0.0
margins[margins <= 0] = 0.0
loss += np.sum(margins) / num_train
loss += 0.5 * reg * np.sum(W * W)
# compute the gradient
margins[margins > 0] = 1.0
row_sum = np.sum(margins, axis=1) # 1 by N
margins[np.arange(num_train), y] = -row_sum
dW += np.dot(X.T, margins)/num_train + reg * W # D by C
return loss, dW
还没试一下,近期试一下这个的结果
标签:not python returns init 公式 技术 min mini sum
原文地址:https://www.cnblogs.com/chenyusheng0803/p/10129202.html