标签:ast 一个 pop other set androi ase maximum insert
Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.
Rules for a valid pattern:
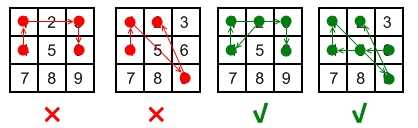
思路:
1. 求路径可行性,需要返回 —— 回溯
2. 用过的不能再用—— map
3. 下面是遍历1-9的做法,其实对称性可以看出1,3,7,9是一样的数量,2,4,6,8是一样数量,5单独一个数量。这样只用算三个数量即可。有时间实现。
1 class Solution { 2 public: 3 int numberOfPatterns(int m, int n) { 4 if (m > 9 || m < 1 || n > 9 || n < 1) return 0; 5 vector<int> path; 6 int ret = 0; 7 set<int> used; 8 helper(m, n, path, used, ret); 9 return ret; 10 } 11 void helper(int m, int n, vector<int> path, set<int> used, int& ret) { 12 if (used.size() >= m && used.size() <= n) ret++; 13 if (used.size() == n) return; 14 for (int i = 1; i <= 9; i++) { 15 if(used.count(i)) continue; 16 if (path.empty()) { 17 path.push_back(i); 18 used.insert(i); 19 helper(m, n, path, used, ret); 20 path.pop_back(); 21 used.erase(i); 22 } 23 else { 24 bool cond1 = path.back() % 2 == 1 && i == 5; 25 bool cond2 = path.back() == 5; 26 bool cond3 = path.back() % 2 == 1 && i % 2 == 1 && path.back() != 5 && used.count((path.back() + i) / 2) != 0; 27 bool cond4 = path.back() % 2 == 1 && i % 2 == 0; 28 bool cond5 = path.back() % 2 == 0 && (path.back() + i) / 2 == 5 && used.count(5) != 0; 29 bool cond6 = path.back() % 2 == 0 && (path.back() + i) != 10; 30 if (cond1 || cond2 || cond3 || cond4 || cond5 || cond6) { 31 path.push_back(i); 32 used.insert(i); 33 helper(m, n, path, used, ret); 34 path.pop_back(); 35 used.erase(i); 36 } 37 } 38 } 39 } 40 };
LC 351. Android Unlock Patterns
标签:ast 一个 pop other set androi ase maximum insert
原文地址:https://www.cnblogs.com/ethanhong/p/10134784.html