算法第5章上机实践

标签：img   图片   0-1背包   好的   上界   sum   实验   代码   难点   

1.实践题目 ：工作分配问题

2.问题描述

　　设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为cij 。 设计一个算法，对于给定的工作费用，为每一个人都分配1 件不同的工作，并使总费用达到最小。

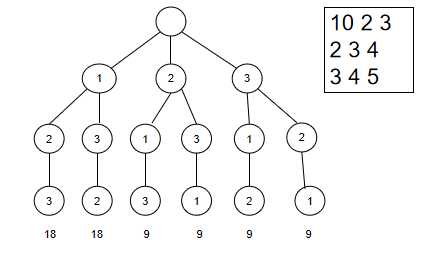
3.算法描述（包括解空间，画出测试样例的解空间树，剪枝（约束函数或限界函数）方法描述

• 解空间：(a₁,a₂,a₃,......,an),a₁表示第一个人被分配的工作序号，以此类推。
• 测试样例的解空间树：如图：

• 约束函数：

  for(int i=t;i<=n;i++)
  {
  if(sum+c[t][a[i]]>m)  //当当前工作费用与下一个待分配工作费用大于已知的可行解的费用，则无需对其及其子树进行遍历，即剪枝
  continue;
  else
  {
  sum += c[t][a[i]];
  swap(a[i],a[t]);
  backtrack(t+1);
  swap(a[i],a[t]);
  sum -= c[t][a[i]];
  }
  }

4.心得体会（对本次实践收获及疑惑进行总结）

　　本次上机实验让我对回溯法有了进一步的了解，尽管回溯法的原理比较简单且解题时可以套一个模板，但有许多需要注意的细节，如：约束函数的位置，回溯代码的“对称性”等。在工作分配问题中，开始时我只设了一个数组以保存“工作i分配给第j个人所需的费用”，然后直接对该数组进行交换，此时我没想清楚这无法保证“每一个人都分配1 件不同的工作”，但由于样例碰巧通过，所以花了很长时间去找到错误的根源。后来看了网上的代码，我才意识到要另设一个一维数组来做交换。

　　原来错误的代码：

else
{
sum += c[t][i];
swap(c[t+1][i],c[t+1][t]);
backtrack(t+1);
swap(c[t+1][i],c[t+1][t]);
sum -= c[t][i];
}

　　0-1背包问题同样花了我很长时间去解题，但最终仍对它的限界函数存有疑惑，我不明白的点在于：既然不允许只放物品的一部分，为什么上界更好的方法是“将剩余物品依次按照单位质量价值排序，然后依次装入物品，直至装不下时，再装入物品的一部分以装满背包，由此得到右子树中解的上界”？

　　我认为回溯法的算法的难点在于分析其解空间以及找到合适的剪枝方法。

算法第5章上机实践

标签：img   图片   0-1背包   好的   上界   sum   实验   代码   难点   

原文地址：https://www.cnblogs.com/Lucy1234567/p/10147059.html