标签：结果   ima   遍历路径   llb   顺序   binary   javascrip   .com   最大   

1.简述

二叉搜索树树（Binary Search Tree），它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

2.代码说明

首先先创建一个辅助节点类Node,它初始化了三个属性：节点值，左孩子，有孩子。

 class Node {
    constructor(value) {
      this.value = value;
      this.left = null;
      this.right = null;
    }
  }

接着创建一个二叉搜索树类BST，它初始化了根节点为null。

class BST {
    constructor() {
      this.root = null;
    }
  }

然后，给这个BST类声明一些方法：

• insert(value):向树中插入一个节点值为value的节点。
• midOrderTraverse(callback)：中序遍历树，并将树中的每个节点传入callback回调函数里。
• preOrderTraverse(callback)：前序遍历树，并将树中的每个节点传入callback回调函数里。
• lastOrderTraverse(callback)：后序遍历树，并将树中的每个节点传入callback回调函数里。
• minNodeInTree()：查找树中节点值最小的节点。
• maxNodeInTree()：查找树中节点值最大的节点。
• searchNodeInTree(value):判断树中是否存在某个节点值为value的节点

3.插入节点

要向树中插入一个新的节点（或项），要经历三个步骤。

1. 第一步是创建用来表示新节点的Node类实例。只需要向构造函数传递我们想用来插入树的节点值，它的左指针和右指针的值会由构造函数自动设置为null。
2. 第二步要验证这个插入操作是否为一种特殊情况。这个特殊情况就是我们要插入的节点是树的第一个节点。如果是，就将根节点指向新节点。
3. 第三步是将节点加在非根节点的其他位置。

代码如下：

insert(value) {
      var newNode = new Node(value);//实例化一个新节点
      var root = this.root;
      if (root == null) {           //如果根节点不存在
        this.root = newNode;        //将这个新节点作为根节点
      } else {                      //如果根节点存在
        insertNode(root, newNode);  //将这个新节点在根节点之后找到合适位置插入
      }
    }

如果是将节点加在非根节点的其他位置，那么这里为了方便起见，我们创建一个辅助函数：insertNode(node,newNode);

• 如果树非空，需要找到插入新节点的位置。因此，在调用insertNode方法时要通过参数传入树的根节点和要插入的节点。
• 如果新节点的键小于当前节点的键（现在，当前节点就是根节点），那么需要检查当前节点的左侧子节点。如果它没有左侧子节点，就在那里插入新的节点。如果有左侧子节点，需要通过递归调用insertNode方法继续找到树的下一层。在这里，下次将要比较的节点将会是当前节点的左侧子节点。
• 如果节点的键比当前节点的键大，同时当前节点没有右侧子节点，就在那里插入新的节点。如果有右侧子节点，同样需要递归调用insertNode方法，但是要用来和新节点比较的节点将会是右侧子节点。

/*
*函数名称：insertNode
*函数说明：将新节点newNode插入到node节点之后的合适位置
*函数参数：newNode,要插入的新节点
*        node,node节点
*/
function insertNode(node, newNode) {
//如果newNode节点值小于node节点值，进入node节点左分支
    if (newNode.value < node.value) {
      //如果node节点左孩子为空
      if (node.left == null) {
      //将newNode赋给node节点左孩子，插入完毕。
        node.left = newNode;
      } else {
      //如果node节点左孩子不为空，则继续向左孩子的左孩子递归
        insertNode(node.left, newNode);
      }
    } else {
      if (node.right == null) {
        node.right = newNode;
      } else {
        insertNode(node.right, newNode);
      }
    }
  }

有了插入节点的方法，那么接下来我们就可以创建出一颗二叉搜索树来。

let bst = new BST();
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
console.log(bst)

在控制台打印，我们就可以画出这个树的样子：

3.树的遍历

遍历一棵树是指访问树的每个节点并对它们进行某种操作的过程。访问树的所有节点有三种方式：中序、先序和后序。

3.1中序遍历

中序遍历是一种以上行顺序访问BST所有节点的遍历方式，也就是以从最小到最大的顺序访问所有节点。中序遍历的一种应用就是对树进行排序操作。中序遍历的执行顺序是先访问节点的左侧子节点，然后访问节点本身，最后是右侧子节点，其遍历路径如下图所示：

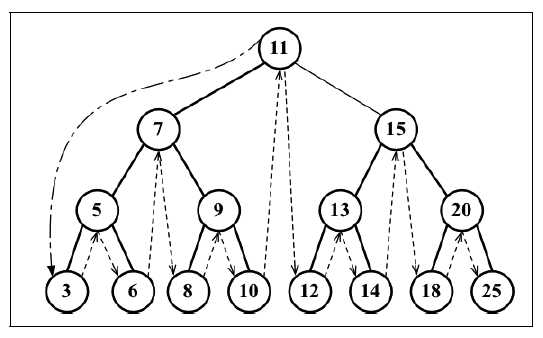
我们编写midOrderTraverse方法实现中序遍历树，该方法收一个回调函数作为参数。回调函数用来定义我们对遍历到的每个节点进行的操作。

// 中序遍历
midOrderTraverse(callback) {
    midOrderTraverseNode(this.root, callback);
}

同时，为了递归方便，编写一个辅助函数midOrderTraverseNode：

// 中序遍历辅助函数
function midOrderTraverseNode(node, callback) {
    if (node !== null) {
        midOrderTraverseNode(node.left, callback);
        callback(node);
        midOrderTraverseNode(node.right, callback);
    }
}

接下来，我们就可以测试一下我们编写代码的功能：以中序遍历上文构建好的二叉搜索树，并打印出每个节点的值。

//打印节点值得函数
function printNode(node) {
    console.log(node.value);
}
bst.midOrderTraverse(printNode)  //中序遍历
//输出结果：
//3 5 6 7 8 9 10 11 12 13 14 15 18 20 25

3.2先序遍历

先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构化的文档。先序遍历会先访问节点本身，然后再访问它的左侧子节点，最后是右侧子节点，其遍历路径如下图所示：

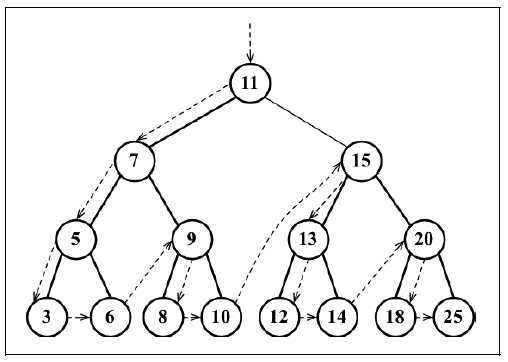
同中序遍历一样，先序遍历还是需要一个辅助函数：

// 先序遍历
preOrderTraverse(callback){
    preOrderTraverseNode(this.root,callback)
}
// 先序遍历辅助函数
function preOrderTraverseNode(node,callback){
    if (node !== null) {
        callback(node);
        preOrderTraverseNode(node.left, callback);
        preOrderTraverseNode(node.right, callback);
    }
}

测试：

//打印节点值得函数
function printNode(node) {
    console.log(node.value);
}
bst.preOrderTraverse(printNode)  //先序遍历
//输出结果：
//11 7 5 3 6 9 8 10 15 13 12 14 20 18 25

3.3后序遍历

后序遍历则是先访问节点的后代节点，再访问节点本身。后序遍历的一种应用是计算一个目录和它的子目录中所有文件所占空间的大小。后序遍历会先访问左侧子节点，然后是右侧子节点，最后是父节点本身。其遍历路径如下图所示：

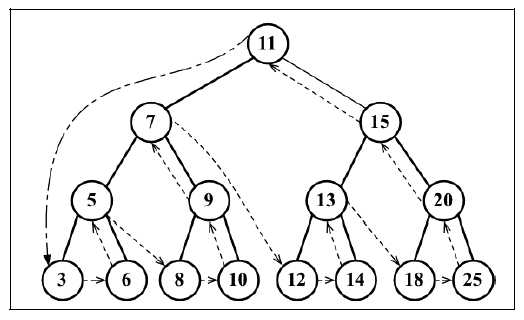
后序遍历还是需要一个辅助函数：

// 后序遍历
lastOrderTraverse(callback){
    lastOrderTraverseNode(this.root,callback)
}
// 后序遍历辅助函数
function lastOrderTraverseNode(node,callback){
    if (node !== null) {
        lastOrderTraverseNode(node.left, callback);
        lastOrderTraverseNode(node.right, callback);
        callback(node);
    }
}

测试：

//打印节点值得函数
function printNode(node) {
    console.log(node.value);
}
bst.lastOrderTraverse(printNode)  //先序遍历
//输出结果：
//3 6 5 8 10 9 7 12 14 13 18 25 20 15 11

3.4总结

通过以上，你会发现，中序、先序和后序遍历的实现方式是很相似的，唯一不同的是访问节点本身、访问左子节点、访问右子节点的顺序。

我们可以这样记忆：

以节点本身为参考，

• 访问顺序为：左——>节点本身——>右，节点本身在中间，即为中序遍历
• 访问顺序为：节点本身——>左——>右，节点本身在最前，即为前序遍历
• 访问顺序为：左——>右——>节点本身，节点本身在最前，即为后序遍历

4.搜索树中的值

4.1搜索树中最小值和最大值

我们知道，在二叉搜索树中，左子节点的值永远小于右子节点的值，所以，树的最小值一定是树的最后一层最左侧的节点，而树的最大值一定是树的最后一层最右侧的节点。

所以，搜索树中的最小值和最大值即就是搜索树中的最后一层最左侧节点和最右侧节点，代码如下：

// 查找树中节点值最小的节点
minNodeInTree(node){
    if (node) {
        while (node && node.left) {
            node = node.left;
        }
        return node.value;
    } else {
        return null;
    }
}
// 查找树中节点值最大的节点
maxNodeInTree(node){
    if (node) {
        while (node && node.right) {
            node = node.right;
        }
        return node.value;
    } else {
        return null;
    }
}

（未完待续。。。）

原生JS实现二叉搜索树（Binary Search Tree）

标签：结果   ima   遍历路径   llb   顺序   binary   javascrip   .com   最大   

原文地址：https://www.cnblogs.com/wangjiachen666/p/10155507.html