机器学习---算法---K-近邻算法

标签：情况下   缩放   ima   htm   倒数   过拟合   算法思想   就是   良好的   

转自：https://www.cnblogs.com/Rosanna/p/3615507.html

 K-近邻和最近邻（K=1）是模式识别中常用的分类方法，K-近邻算法思想是找到与当前样本相邻的K个有标签样本，然后通过投票决定此样本的类别。例如下图中如何分类未知的绿色圆圈呢？

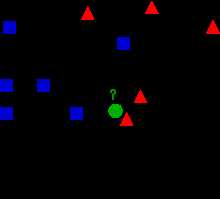
      例如我们可以取K=3个临近的样本时，通过投票（红色两个大于蓝色一个），从而将绿色圆圈归于红色三角一类。

一.基于实例的学习

      K-近邻和局部加权回归就是基于实例的学习。基于实例的学习过程只是简单的存储已知的训练数据，当遇到新的待分类样本时，将从训练数据中挑选出一系列相似的样本，并用来分类新的样本。

      与常见的分类算法（如神经网络）不同的是，基于实例的方法可以为不同的待分类样本建立不同的函数逼近。只建立目标函数的局部逼近，而不是建立在整个样本空间都表现良好的逼近。所以，当目标函数很复杂但可以用不太复杂的局部逼近描述时，用基于实例的学习方法会有很大的优势。

      同时我们可以看到基于实例的学习方法一个很明显的缺点就是它分类新样本开销很大，因为几乎所有的计算都放生在分类时，而不是第一次遇到训练样本时。另外还有一个缺点就是从训练数据中寻找相似样本时，我们一般都是计算样本的所有属性的距离，当样本只依赖于其中几个属性时，新的待分类样本会离真正相似样本很远，从而发生错误分类。

二.K-近邻算法

      假设一个样本的特征向量为{a₁(x),a₂(x),…,a_n(x)}，a_r(x)表示样本x的第r个属性值。那么两个样本xi,xj之间的距离可以表示为

d(xi,xj)=sqrt(sum(a_r(xi)-a_r(x_j))²)   r=1~n

        K-紧邻的算法流程很简单：

• 训练：讲训练样本加入train_set；
• 分类：对一个新的待分类样本x_q
•          计算train_set中最靠近x_q的k个样本，记为x₁，x₂，...，x_k
•          返回最多的类别信息

      关于K值的选择，摘自李航《统计学习方法》：

• 如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
• 如果选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单；
• K=N，则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的累，模型过于简单，忽略了训练实例中大量有用信息。

三.K-近邻算法改进

      针对K-近邻算法的不足可以做出几点改进：

1.距离加权

      本文一开始的示例图中，若K=5，那么绿色圈圈就会被分类到蓝色方块中。为了解决这个问题，可以对K个近邻的贡献加权，权值为距离平方的倒数：

w_i=1/(d(x_i,x_j)²) 

      即距离越远，权值越小，距离越近，权值越大。

2.对每个属性加权

      并不是样本所有的属性都是有助于分类的，例如一个样本由20个属性描述，但这些属性中只有2个与分类有关。在这种情况下，一个测试样本可能在20维的空间中与它想死的训练样本相距很远，结果导致了错误分类。解决的办法就是给每个属性加权，这相当于按比例缩放欧式空间的坐标轴，缩短不太相关的属性的坐标轴，拉长对应于更相关的属性的坐标轴，可以通过交叉验证自动决定。

3.建立索引

      K-近邻推迟了所有的计算，直到来了一个新的测试样本，分类时需要大量计算。一个高效的解决办法就是对存储的训练样本进行索引，在增加一定存储开销的情况下更快速的找到K个临近样本，比如Kd-tree[参考2]。

四.总结

1.KNN的优点：

• 理论成熟，算法简单；
• 可用于非线性分类；
• 对outlier不敏感。

2.KNN的缺点：

• 不平衡样本效果不好；
• 预测计算量大；
• 占用内存多。

参考资料：

1.《机器学习》

2.从K近邻算法、距离度量谈到KD树、SIFT+BBF算法

机器学习---算法---K-近邻算法

标签：情况下   缩放   ima   htm   倒数   过拟合   算法思想   就是   良好的   

原文地址：https://www.cnblogs.com/qing1991/p/10163288.html