标签:image 分享 回溯 count class out 0-1背包 技术 产生
1.实践题目:
设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为cij 。 设计一个算法,对于给定的工作费用,为每一个人都分配1 件不同的工作,并使总费用达到最小。
2.问题描述:
将n份工作分别分配给n个人,每个人分配一份不同的工作,通过某一种分配方式,使得总费用达到最小。
3.算法描述:
代码:
1 #include<iostream> 2 using namespace std; 3 4 int n,cost=0; 5 int x[100],c[100][100]; 6 7 void work(int i,int count) 8 { 9 if(i>n && count<cost) 10 { 11 cost = count; 12 return ; 13 } 14 if(count<cost) 15 for(int j=1;j<=n;j++) 16 if(x[j] == 0) 17 { 18 x[j] = 1; 19 work(i+1,count+c[i][j]); 20 x[j] = 0; 21 } 22 } 23 int main() 24 { 25 cin>>n; 26 for(int i=1;i<=n;i++) 27 { 28 for(int j=1;j<=n;j++) 29 { 30 cin>>c[i][j]; 31 x[j] = 0; 32 } 33 cost+=c[i][i]; 34 } 35 work(1,0); 36 cout<<cost<<endl; 37 return 0; 38 }
解空间树:
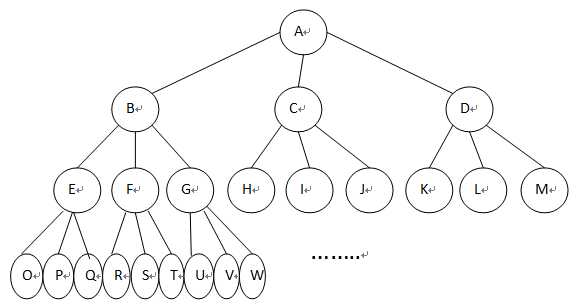
说明:每一层表示给第i个工人分配工作,第一棵子树表示分配工作1,第二棵子树表示分配工作2,第三棵子树表示分配工作3.
剪枝方法:
在每次计算当前产生费用count的值时,比较count和cost(记录最小费用)的大小。如果count已经大于cost,就不用再往下分配了,因为这时得到的解必然不是最优解。
4.心得体会:
在这次实践中,很多同学都卡在了第一题即0-1背包问题,我和我的搭档也是如此,主要问题是剪枝函数,题目要求必须用严格型,否则运行超时,经过讨论分析,我们才把第一题解决了。通过这次的上机实践课,我们对回溯法都有了进一步的理解,以后遇到类似问题时也会提高警惕,科学分析,得到最终的答案,不断提高自己的分析能力、解题能力。
标签:image 分享 回溯 count class out 0-1背包 技术 产生
原文地址:https://www.cnblogs.com/yilun578663140/p/10164762.html