标签:mic bubuko pass eth 试题 有用 父类 符号 ack
一. 经典类和新式类
1.python多继承
在继承关系中,python子类自动用友父类中除了私有属性外的其他所有内容.python支持多继承.一个类可以拥有多个父类
2.python2和python3的区别
python2中存在两种类,一个叫经典类,在python2.2之前,一直使用的经典类.经典类是在基类的根如果什么都不写.表示继承xxx
另一个叫做心事类,在python2.2之后出现了心事类.新式类的特点是基类的根是object
python3中使用的都是新式类.如果基类谁都不继承,那这个类会默认继承object
二. 经典类的MRO
1. 经典类的MRO 树型结构的深度优先遍历 --> 树形结构遍历
class Foo:
pass
class Foo(object):
pass
MRO: method resolution order 方法的查找顺序
class Base:
pass
class Base1:
def chi():
pass
class Bar(Base, Base1):
pass
b = Bar() # Bar -> Base -> Base1
b.chi()
再举一个例子
class A:
pass
class B(A):
pass
class C(A):
pass
class D(B, C):
pass
class E:
pass
class F(D, E):
pass
class G(F, D):
pass
class H:
pass
class Foo(H, G):
pass
来看关系图
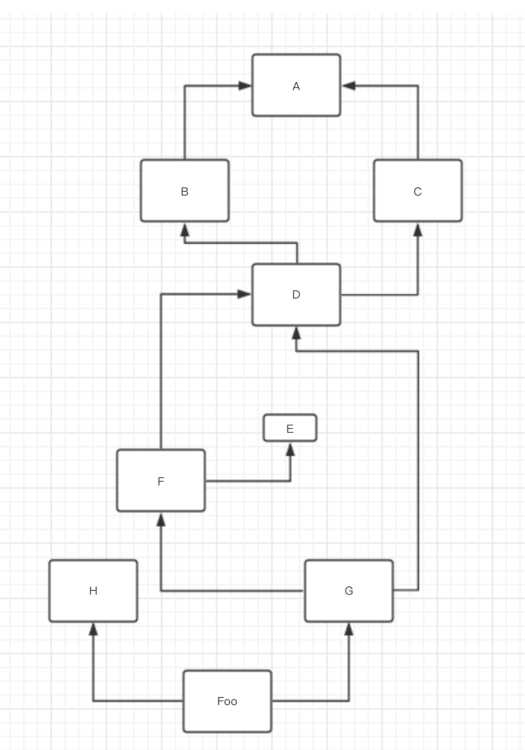
进行深度优先遍历
MRO: Foo-> H -> G -> F -> D -> B -> A -> C -> E.
2. 新式类的MRO C3算法
C3方法解决顺序
让我介绍几个简单的符号,这些符号对以下讨论很有用。我将使用快捷方式表示法
C1 C2 ... CN
表示类别列表[C1,C2,...,CN]。
列表的头部是它的第一个元素:
head = C1
而尾巴是列表的其余部分:
tail = C2 ... CN。
我也会用这个符号
C +(C1 C2 ... CN)= C C1 C2 ... CN
表示列表的总和[C] + [C1,C2,...,CN]。
现在我可以解释MRO如何在Python 2.3中运行。
考虑多继承层次结构中的C类,其中C继承自基类B1,B2,...,BN。我们想要计算C类的线性化L [C]。规则如下:
C的线性化是C的总和加上父母的线性化和父母的列表的合并。
用符号表示法:
L [C(B1 ... BN)] = C +合并(L [B1] ... L [BN],B1 ... BN)
特别是,如果C是没有父项的对象类,则线性化是微不足道的:
L [object] =对象。
但是,通常必须根据以下处方计算合并:
取第一个列表的头部,即L [B1] [0]; 如果这个头不在任何其他列表的尾部,那么将它添加到C的线性化并将其从合并中的列表中删除,否则查看下一个列表的头部并将其取出,如果它是好头。然后重复操作,直到所有课程都被移除或者找不到好头。在这种情况下,不可能构造合并,Python 2.3将拒绝创建类C并将引发异常。
如果可以保留排序,则此处方确保合并操作保留排序。另一方面,如果无法保留订单(如上面讨论的严重订单不一致的例子),则无法计算合并。
如果C只有一个父(单继承),那么合并的计算是微不足道的。在这种情况下
L [C(B)] = C +合并(L [B],B)= C + L [B]
官网解释 https://www.python.org/download/releases/2.3/mro/
举例说明
class A:
pass
class B(A):
pass
class C(A):
pass
class D(B, C):
pass
class E(C, A):
pass
class F(D, E):
pass
class G(E):
pass
class H(G, F):
pass
首先确定的是要找的H
把每个类转换为C3算法的形式
L(A) = A
L(B) = B + L(A) + A
L(C) = C + L(A) + A
L(D) = D + L(B) + L(C) + BC
L(E) = E + L(C) + L(A) + CA
L(F) = F + L(D) + L(E) + DE
L(G) = G + L(E) + E
L(H) = H + L(G) + L(F) + GF
之后我们来化简
加法:merge(), 拿第一项的第一位和 后面每项的除了第一位比较. 如果没有出现, 则该位元素算出
如果出现了. 此时开始下一项的第一位继续和后面每一项的除了第一位比较:
L(A) = A
L(B) = B + L(A) + A = BC
L(C) = C + L(A) + A = CA
L(D) = D + L(B) + L(C) + BC = D + BC + CA = DBCA
L(E) = E + L(C) + L(A) + CA = E + CA + A + CA = ECA
L(F) = F + L(D) + L(E) + DE = F + DBCA + ECA = FDBECA
L(G) = G + L(E) + E = G +ECA + E = GECA
L(H) = H + L(G) + L(F) + GF = H + GECA + FDBECA + GF = HGFDBECA
三. super
super() 找MRO顺序的下一个
来看一道面试题
# MRO + super ?面试题
class Init(object):
def __init__(self, v):
print("init")
self.val = v
class Add2(Init):
def __init__(self, val):
print("Add2")
super(Add2, self).__init__(val)
print(self.val)
self.val += 2
class Mult(Init):
def __init__(self, val):
print("Mult")
super(Mult, self).__init__(val)
self.val *= 5
class HaHa(Init):
def __init__(self, val):
print("哈哈")
super(HaHa, self).__init__(val)
self.val /= 5
class Pro(Add2,Mult,HaHa): #
pass
class Incr(Pro):
def __init__(self, val):
super(Incr, self).__init__(val)
self.val+= 1
# Incr Pro Add2 Mult HaHa Init
p = Incr(5)
print(p.val)
c = Add2(2)
print(c.val)
先算出MRO
L(Init) = Init
L(Add2) =Add2 + L(Init) + Init = Add2 , Init
L(Mult) = Mult + L(Init) + Init = Mult ,Init
L(HaHa) = HaHa + L(Init) + Init = HaHa,Init
L(Pro) = Pro +L(Add2) + L(Mult) + L(HaHa) + Add2,Mult,HaHa = Pro + Add2 , Init + Mult ,Init + HaHa,Init + Add2,Mult,HaHa = Pro,Add2,Mult,HaHa,Init
再进行运算

标签:mic bubuko pass eth 试题 有用 父类 符号 ack
原文地址:https://www.cnblogs.com/robertx/p/10169427.html