标签:each 数据 数据结构 ons 循环 length oat img str

| 数据结构 | 数组 |
|---|---|
| 最差时间复杂度 | O(n^2) |
| 最优时间复杂度 | O(n) |
| 平均时间复杂度 | O(n^2) |
| 最差空间复杂度 | 总共O(n),需要辅助空间O(1) |
思路和代码:
//假如有几个数字 按照从小到大排序。有2种思路
public static int[] arr = new int[] { 74, 88, 69, 67, 75 };
public static int[] arr2 = new int[] { 74, 88, 69, 67, 75 };
//第一种,arr[j] 和arr[j + 1] 比较 如果 前者比后者大,把前者和后者调换顺序,两两调换后一轮下来 最大的会被排到最后去。外层循环arr.length-1次。
//每一轮j都从0开始,每次i轮排序,后面的i个数字已经是排好的,所以后面的每轮都不用理他了,也就是 arr.length-1-i 往后的数不用管了。
//如上:
//第一轮有4个数字 i为0 ,那么arr.length-1-i 为3,也就是下标是3以后的可以不用管,3往后没有数字,所以第一轮所有的数字都要参加比较。
//实现代码如下:
public static void Order()
{
int iCount = 0;
for (int i = 0; i < arr.Length - 1; i++)
{
iCount++;
int jCount = 0;
for (int j = 0; j < arr.Length - i - 1; j++)
{
jCount++;
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
Console.WriteLine($"i:{iCount} j:{jCount}");
}
arr.ToList().ForEach((x) =>
{
Console.WriteLine(x);
});
}
//第二种思路,由后向前比较,最小的会排在最前面
public static void Order2()
{
int iCount = 0;
for (int i = 0; i < arr2.Length - 1; i++)
{
iCount++;
int jCount = 0;
for (int j = arr2.Length - 1; j > i; j--)
{
jCount++;
if (arr2[j] < arr2[j - 1])
{
int temp = arr2[j];
arr2[j] = arr2[j - 1];
arr2[j - 1] = temp;
}
}
Console.WriteLine($"i:{iCount} j:{jCount}");
}
arr2.ToList().ForEach((x) =>
{
Console.WriteLine(x);
});
}
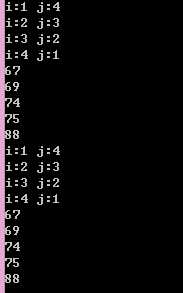
结果:
标签:each 数据 数据结构 ons 循环 length oat img str
原文地址:https://www.cnblogs.com/luanxm/p/10200519.html