标签:return show can 有向无环图 pos aaa [1] href 指针
我还什么都不会啊
字符串还是很重要的,省选肯定会考的吧
所以还是先写一下马拉车吧
$ $
是一个求最长回文子串的算法,复杂度\(O(n)\)
核心原理就是利用回文串的性质
首先还是按照对称轴来找回文串,为了避免分类讨论回文串的奇偶性,所以可以在字符串之间先填充特殊字符
具体做法就是倍长原来的字符串,在第\(0\)位和最后一位填上特殊字符作为边界,之后原来每一个字符之间也填充上特殊字符
比如\(abaaa\),就会被填充成为\(\#a\#b\#a\#a\#a\#\)
显然偶数位置会是特殊字符,而奇数位置则是原来的字符
之后是具体的工作原理也很简单
在过程中我们存一个当前扩展出的回文串中最靠右的在哪里,用\(R\)表示,\(mid\)表示当前回文串的对称轴在哪里,用\(r[i]\)表示\(i\)这个位置能够形成的最长的回文半径是多少,也就是最多能向左右同时扩展多少位
对于一个新扩展的位置\(i\),显然是要大于\(mid\)的,如果这个时候\(i<=R\)那么就有一个非常显然的性质,就是在这个以\(mid\)为轴的回文串里,和\(i\)对称的位置\(j\),一定存在\(r[i]>=r[j]\)
非常显然\(j=mid*2-i\)
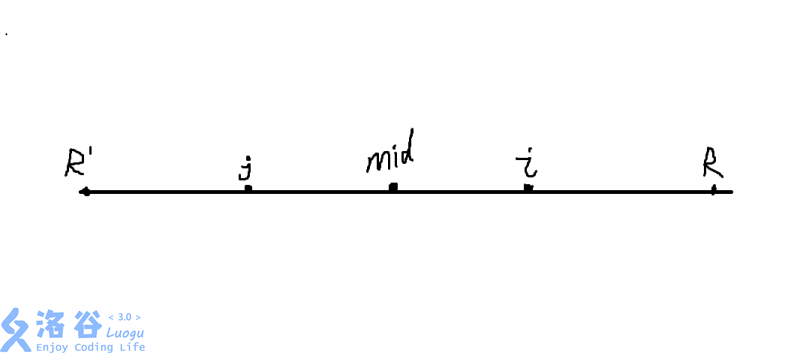
显然由于\([R‘,R]\)都是一个回文串,所以会满足\(S[i+1]=S[j-1]\),\(S[i-1]=S[j+1],S[i+2]=S[j-2],S[i-2]=S[j+2]...\),也就是说只要没超过当前的这个\(R\),都会满足这样的性质,但是这样最多也只能扩展到\(R\)位置
我们可以直接让\(r[i]=min(r[j],R-i)\),之后往左右两边暴力扩展就好了
如果\(r[i]+i>R\)了,我们就更新\(R\)和\(mid\),最后所有\(r[i]\)的最大值就是答案了
板子
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 11000005
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
char S[maxn<<1];
int r[maxn<<1];
int n,ans;
int main()
{
scanf("%s",S+1);
n=strlen(S+1)<<1;
for(re int i=n-1;i>1;i-=2) S[i]=S[(i>>1)+1];
for(re int i=n;i;i-=2) S[i]=0;
int mid=1,R=1;
for(re int i=1;i<=n;i++)
{
if(i<=R) r[i]=min(r[(mid<<1)-i],R-i);
for(re int j=r[i]+1;j<=i&&j<=n&&S[i+j]==S[i-j];j++) r[i]=j;
if(i+r[i]>=R) R=i+r[i],mid=i;
ans=max(ans,r[i]);
}
std::cout<<ans;
return 0;
}这个就真的是神仙操作了
我还是只会后缀排序
后缀排序的意思就是给出一个字符串,把它的所有后缀按照字典序来排序
具体后缀排序的思路就不讲了,放一个很好的链接吧
之后可能看了这个还是一脸蒙蔽
于是放上加了很多注释的板子
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 1000005
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define pt putchar(1)
inline int read()
{
char c=getchar();int x=0;
while(c<‘0‘||c>‘9‘) c=getchar();
while(c>=‘0‘&&c<=‘9‘) x=(x<<3)+(x<<1)+c-48,c=getchar();return x;
}
int rk[maxn],tp[maxn],sa[maxn],tax[maxn];
//sa[i]表示排名为i的后缀
//rk[i]表示后缀i的排名
int n,m;
char S[maxn];
inline void qsort()
{
for(re int i=0;i<=m;i++) tax[i]=0;
for(re int i=1;i<=n;i++) tax[rk[i]]++;//统计第一关键字的数量
for(re int i=1;i<=m;i++) tax[i]+=tax[i-1];//做一个前缀和,可以快速的确定每一种第一关键字所对应的最后的位置是多少
for(re int i=n;i;--i) sa[tax[rk[tp[i]]]--]=tp[i];
//这里比较复杂了
//从里面一步一步的推吧
//首先我们倒着循环的,也就是按照第二关键字从大往小的顺序
//rk[tp[i]当前对应的桶是多少
//由于我们是倒着循环的,所以肯定是当前桶里最大的一个,自然要放在桶里最靠前的位置
}
int main()
{
scanf("%s",S+1);
n=strlen(S+1);
for(re int i=1;i<=n;i++)
rk[i]=S[i]-‘0‘,tp[i]=i;
m=75;
qsort();
for(re int w=1,p=0;p<n;m=p,w<<=1)
//w表示当前的已经处理好的长度,也就是对于每个后缀来说往后数w位在当前的sa里是有序的
//p表示当前一共有多少种不同的第一关键字,当p=n的时候就意味着已经排好序了
{
p=0;
for(re int i=1;i<=w;i++) tp[++p]=n-w+i;
//这里是把最后的w位加进来,这些位置的第二关键字都是0
for(re int i=1;i<=n;i++) if(sa[i]>w) tp[++p]=sa[i]-w;
//tp[i]表示第二关键字排名为i的位置,也就是哪一个位置+w对应的sa是i
qsort();
for(re int i=1;i<=n;i++) std::swap(tp[i],rk[i]);
//tp已经没有什么用了,于是用来存一下上次的rk
rk[sa[1]]=p=1;
for(re int i=2;i<=n;i++)
rk[sa[i]]=(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+w]==tp[sa[i]+w])?p:++p;
//更新rk,如果本次排序还没有区分出来,那么p不变,否则就有一个新的接下来排序需要的第一关键字了
}
for(re int i=1;i<=n;i++) printf("%d ",sa[i]);
return 0;
}之后着重说一下\(height\)数组这个神奇的东西
\(height[i]=lcp(sa[i],sa[i-1])\)也就是\(height[i]\)表示排名为\(i\)的后缀和排名为\(i-1\)的后缀的最长公共前缀的长度
\(height\)数组如何快速求出呢,反正我只会背板子
从学长那里抄来一个证明
首先我们不妨设第i-1个字符串按排名来的前面的那个字符串是第k个字符串,注意k不一定是i-2,因为第k个字符串是按字典序排名来的i-1前面那个,并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。
这时,依据height[]的定义,第k个字符串和第i-1个字符串的公共前缀自然是height[rk[i-1]],现在先讨论一下第k+1个字符串和第i个字符串的关系。
第一种情况,第k个字符串和第i-1个字符串的首字符不同,那么第k+1个字符串的排名既可能在i的前面,也可能在i的后面,但没有关系,因为height[rk[i-1]]就是0了呀,那么无论height[rk[i]]是多少都会有height[rk[i]]>=height[rk[i-1]]-1,也就是h[i]>=h[i-1]-1。
第二种情况,第k个字符串和第i-1个字符串的首字符相同,那么由于第k+1个字符串就是第k个字符串去掉首字符得到的,第i个字符串也是第i-1个字符串去掉首字符得到的,那么显然第k+1个字符串要排在第i个字符串前面。同时,第k个字符串和第i-1个字符串的最长公共前缀是height[rk[i-1]],
那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rk[i-1]]-1。
到此为止,第二种情况的证明还没有完,我们可以试想一下,对于比第i个字符串的排名更靠前的那些字符串,谁和第i个字符串的相似度最高(这里说的相似度是指最长公共前缀的长度)?显然是排名紧邻第i个字符串的那个字符串了呀,即sa[rank[i]-1]。但是我们前面求得,有一个排在i前面的字符串k+1,LCP(rk[i],rk[k+1])=height[rk[i-1]]-1;
又因为height[rk[i]]=LCP(i,i-1)>=LCP(i,k+1)
所以height[rk[i]]>=height[rk[i-1]]-1,也即h[i]>=h[i-1]-1。那么这个\(height\)数组有什么用呢,非常显然可以用来求两个后缀的\(lcp\)啊
对于两个后缀\(i,j\),约定\(rk[i]<rk[j]\),他们的\(lcp\)长度就是
\[min(height[rk[i]+1]...height[rk[j]])\]
也就是说可以通过\(rmq\)快速求出两个后缀的\(lcp\)长度
利用这个性质还是有一些题目的
可能还会和一些数据结构套在一起,比如说单调栈,主席树,\(st\)表之类的
之后是后缀数组的几个非常经典的应用(都是从论文里抄的自然非常经典了)
这个非常好做,显然答案就是\(height\)数组里的最大值
这个就比刚才那个多了一个限制,就是\(sa[i]+lcp(i,j)<=sa[j]\)
这里需要用到一个经典的套路,就是二分之后对\(height\)分组
显然答案存在单调性,所以我们现在要判断的是是否存在一个长度为\(mid\)的不重叠子串
我们可以对\(het\)数组分组,使得一个组内部的\(het\)都大于等于\(mid\),之后我们从这个组里找到最大和最小的\(sa\),如果差超过\(mid\),就代表答案合法了
和上面是一个套路,我们还是二分一个答案\(mid\),之后对\(height\)分组,之后我们判断一个组内部的数量时候大于等于\(k\)就好了
这类的题也有一些
这个直接写了题解了
这样的题好像也不少啊,但是我就没做多少
我怎么可能学会这么神仙的东西
\(SAM\)是一个非常强大的自动机,可以直接匹配一个串的所有子串,就是那种完全不需要动脑子直接放在自动机上跑一跑的那种
一个\(SAM\)由两个结构组成:一个是一张有向无环图(\(DAWG\)),之后就是一棵\(parent\)树
\(SAM\)的任何一个节点都可以同时在这两种结构上被找到
但是一个字符串的所有子串数目高达\(n^2\)级别,如何用尽量少的字符使得自动机能匹配所有子串是一个非常优雅的问题
显然必须得把一些信息压缩起来处理
而\(SAM\)上的一个节点表示的,则是一个或者多个子串,因为从最开始的状态出发,可以到这个节点的路径有很多种,每一条路径都可以表示一个子串
而一个节点所表示的所有子串,都必定是一个某一个前缀的一些后缀,且这些前缀的后缀的长度都相差\(1\)
算了还是决定正儿八经写一下\(SAM\)这个东西了
先讲一下几个非常重要的概念吧
每个\(DAWG\)上的节点都会对应一个\(endpos\)集合,其含义是这个节点所表示的最长的子串在整个字符串里出现的结束位置
比如说母串是\(abcbca\),那么\(endpos(bc)=\{3,5\}\),\(endpos(a)=\{1,5\}\)
在一个\(SAM\)上没有两个节点的\(endpos\)集合是相同的,因为\(SAM\)上的节点表示的是一个\(endpos\)等价集合,相等的\(endpos\)会被合并在一起
之后关于\(endpos\)有几条显然的性质
\[endpos(w)\subseteq endpos(u)(u\text{是}w\text{的后缀})\]
\[endpos(w)\cap endpos(u)=\oslash (u\text{不是}w\text{的后缀})\]
于是我们定义\(min(v)\)表示\(v\)这个节点所代表的\(endpos\)等价类中的最短长度也就是\([x,y]\)里的\(x\),\(len(v)\)表示最长长度也就是\(y\)
有什么用吗,接下来肯定有用了
这个是\(parent\)树上的东西了,或者说\(parent\)根本就是靠着这个搭起来的
先来看看定义吧
\(u\)的最大值加一恰好能和\(v\)的最小值连接起来,也就是说明如果\(u\)的子串长度区间是\([x_1,y_1]\),\(v\)是\([x_2,y_2]\),那么两个就可以连起来了,变成\([x_1,y_2]\),于是通过\(parent\)树上反复向上跳我们就能把每一个后缀的所有前缀都访问一遍
换句话说我们从\(v\)在\(parent\)树上跳\(link\)最后得到的区间是\([0,len(v)]\)
看起来还是很鸡肋的性质,但是接下来就非常有用了
其实也不是特别麻烦
\(SAM\)的构建采取的是增量算法,就是每次都往\(SAM\)里添加一个字符,添加到最后的时候就会得到整个串的\(SAM\)了
考虑我们每次插入会产生那些子串
一个新的前缀
这个新的前缀的所有后缀
简单描述一下算法过程吧
设当前加入的字符为\(c\),建立一个新节点\(p\),这个新节点要继承上一次加入的节点的状态,于是\(len(p)=len(last)+1\),这样的话我们就新成立了一个\(endpos\)等价类,也完成了插入一个新的前缀的工作
之后要插入这个新的前缀的所有后缀,设\(f=last\),\(last=p\),之后往上一直对\(f\)跳\(link\),如果当前的\(f\)没有\(c\)这个转移我们就给它加上,表示我们插入了这个新前缀的一些后缀,跳到\(parent\)树上的根或者跳到\(f\)有\(c\)这个儿子为止
到现在我们要插入的所有新的子串都插入完了,之后就是要给新插入的\(p\)找一个\(link\)了
如果跳到了根,那么\(link(p)=1\)退出就好了
否则的话我们就设\(x\)为当前\(f\)的\(c\)转移,可能我们的\(link(p)\)就是\(x\)了,但是别忘了我们的\(link\)必须得满足一个条件,就是\(len(x)+1=min(p)\),这个时候\(min(p)\)肯定是\(len(f)+2\)了,这显然是最小的长度了,所以我们必须要使得\(len(x)=len(f)+1\),如果\(len(x)\)这是时候正好是\(len(f)+1\),我们就直接\(link(p)=x\)之后退出就好了
否则的话情况就非常棘手了,我们得强行使得\(len(x)=len(f)+1\),但又得遵循原来的\(len(x)\),于是我们再新开一个节点\(y\),令\(y\)继承\(x\)的所有状态,但是\(len(y)=len(f)+1\),这个时候\(link(p)=y\)就可以啦
这还没完,我们还得一路把\(f\)改上去,如果到\(c\)的转移是\(x\)我们就把它更新成\(y\)
之后终于没了
把自己的板子放上去吧
inline void ins(int c)
{
int f=lst,p=++cnt; lst=p;
len[p]=len[f]+1,sz[p]=1;
while(f&&!son[f][c]) son[f][c]=p,f=link[f];
if(!f){link[p]=1;return;}
int x=son[f][c];
if(len[x]==len[f]+1) {link[p]=x;return;}
int y=++cnt;
len[y]=len[f]+1,link[y]=link[x],link[p]=link[x]=y;
for(re int i=0;i<26;i++) son[y][i]=son[x][i];
while(f&&son[f][c]==x) son[f][c]=y,f=link[f];
}标签:return show can 有向无环图 pos aaa [1] href 指针
原文地址:https://www.cnblogs.com/asuldb/p/10205581.html