标签:scan 逆序 对应关系 图像 完全 关系 运算 定义 没有
都应该知道多项式是什么对吧(否则学什么多项式乘法)
我们用\(A(x)\)表示一个\(n-1\)多项式,即\(A(x)=\sum_{i=0}^{n-1} {a_i}*x^i\)
例如\(A(x)=x^2+3x+1\)就是一个\(x\)的二次多项式
多项式的加减都接触过,就是合并同类项的过程
乘法也很简单,就是初中的化简式子题
那么计算两个多项式相乘的时间复杂度是什么呢?
如果我们用初中学到的暴力拆括号法,第一个括号里的每一项都要与第二个括号了的项相乘,时间复杂度显然是\(O(n^2)\)的,看上去就十分糟糕
于是人们发明了FFT
那么又有新问题了,如果所有的系数对一个数取余呢?(这一点在生成函数中尤为关键)
于是人们又发明了NTT
我们先来了解一下FFT,不过在此之前,我们最好了解一下以下内容——
先看这样一个问题:对于两个未知数\(x,y\),我至少要给你多少个方程你才能解出\(x,y\)的值?很明显至少要两个
这又是一个初中的结论的:\(n\)个未知数我们至少需要\(n\)个方程来求值
这给了我们一个新的表示一个多项式的方法,对于任意一个\(n-1\)次的多项式\(A(x)\)而言,加入我们知道了对于\(n\)个不同的\(x\)的取值的多项式的取值\(y\),即已知了函数图像上的\(n\)个点\((x_1,y_1),(x_2,y_2),\cdots ,(x_n,y_n)\),那么这个\(A(x)\)的解析式就应该是确定的了
很明显的发现,对于两个多项式\(A(x)\)和\(B(x)\),令\(C(x)=A(x)*B(x)\),假设最终的\(C(x)\)是\(n-1\)次的,那么我们可以任取\(n\)个不相同的\(x\)的值代入\(A(x)\)和\(B(x)\)中,得到它们的点值表示,对于它们的某一组\(x\)值相同的点值\((x_i,A_i),(x_i,B_i)\),会有\((x_i,A_iB_i)\)成立,因此我们可以在\(O(n)\)的时间内求得两个多项式的乘积
但这又一个前提——开始的\(A(x)\)和\(B(x)\)均为点值表达式。如果是最为人熟悉的系数表达式的话就要进行转化,将一个\(x\)代入求值需要\(O(n)\)的时间,所以朴素的求出某个多项式的点值表达式又是\(O(n)\)的
诶这和最开始的做法有什么区别啊QAQ
但这里至少有一个可以优化的地方——我们如何快速的将一个系数表达式转化成点值多项式。和明显代入值是无法避免的,所以只能对代入的\(x\)进行优化了
所以丧心病狂的学者们找到了下面这个好东西——单位根,但在了解单位根之前,我们先要知道
日常打成负数,两者是完全不一样的
最直观的理解复数可以从这个问题入手:我们知道\(\sqrt 9=3\),那么\(\sqrt {-9}\)等于什么呢?很明显答案不是3或-3
于是无所事事的数学家发明了一个新的数——虚数,写作\(i\),这个数满足\(i^2=-1\)
然后将它和实数写在一起即\(a+bi\)(a,b均为实数),并将这一坨东西叫做复数
后来,人们又魔改了笛卡尔坐标系,将原来的\(x\)轴作为实轴,原来的\(y\)轴作为虚轴,于是虚数就被表示成了这个坐标轴上的一个点(也可以理解成向量),这个坐标轴也被叫做复平面。我们之后要提到的单位根,就和这个复平面有关
但在这之前,我们先来开一下与复数有关的运算
在c++中定义了虚数类型的库
#include<complex>不过由于这玩意自带大常数,所以建议还是自己手打复数+重载运算符
复数的加减十分简单:
\[
(a+bi)\pm(c+di)=(a\pm c)+(b\pm d)i
\]
乘法也是一样的,直接拆开即可
\[
(a+bi)*(c+di)=ac+adi+bc-bd=(ac-bd)+(ad+bc)i
\]
这个东西在坐标系中表现为:模长相乘,幅角相加
把上面的东西整理一下得到如下的代码
struct complex{
double x,y;
complex(double x1=0.0,double y1=0.0) {x=x1,y=y1;}
};
complex operator +(complex a,complex b)
{
return complex(a.x+b.x,a.y+b.y);
}
complex operator -(complex a,complex b)
{
return complex(a.x-b.x,a.y-b.y);
}
complex operator *(complex a,complex b)
{
return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}(从这里开始的所有论述中,均保证\(n=2^k(k\in Z)\),你往下看就会发现这极大地简化了运算)
考虑一些数\(z\)满足\(z^n=1\),那么这些\(z\)就被叫做单位根,它有一些很神奇的性质
我们考虑在复平面中的单位圆,并将其分成\(n\)等分(如下图\(n=4\))
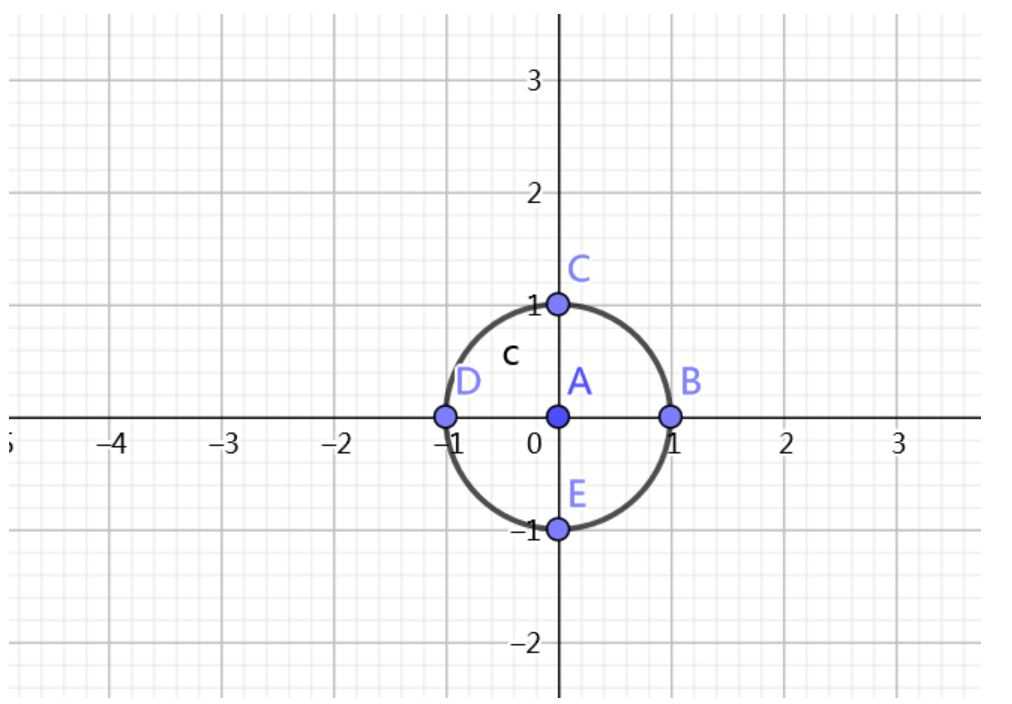
得到的这些点就是上面提到的单位根,记做\(w_n^0,w_n^1,\cdots,w_n^{n-1}\),且\(w_n^0=1\)
我们来考虑一下它们的通项公式,由下面的图应该会有
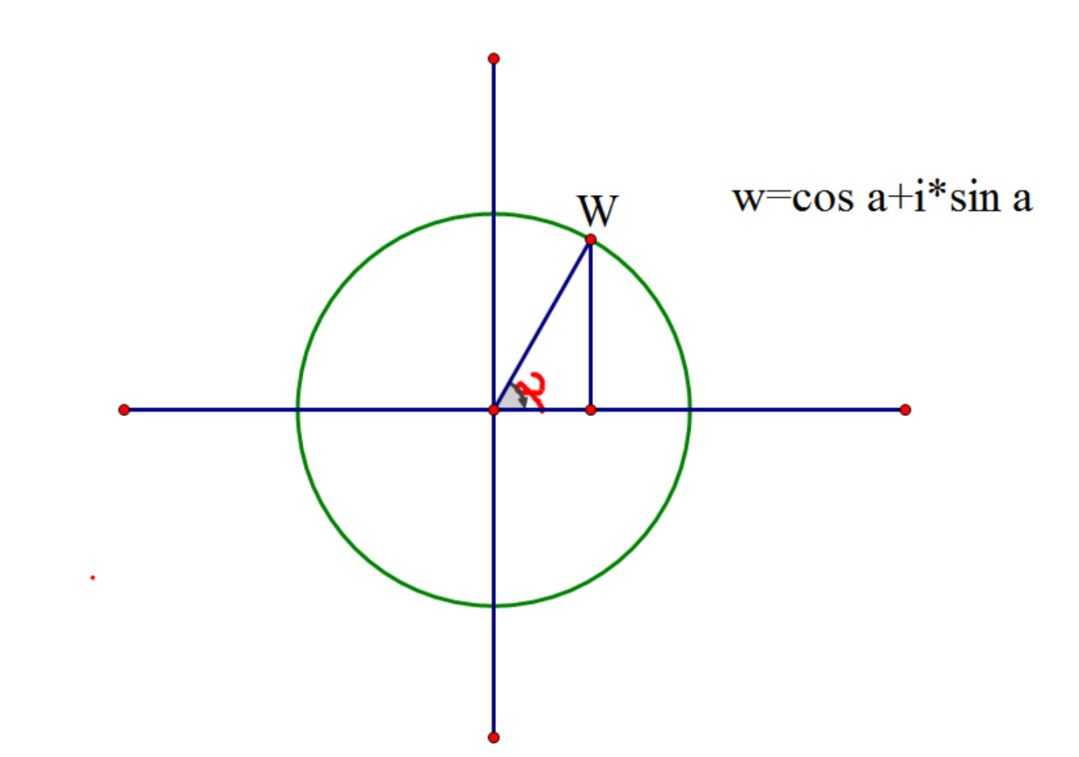
将其用弧度制表示便有
\[
w_n^k=cosk*\frac{2\pi}{n}+isink*\frac{2\pi}{n}
\]
我们把这样的\(w_n^0,w_n^1,\cdots,w_n^{n-1}\)代入到多项式\(A(x)\)中得到对应的值,这个过程叫做DFT(离散傅里叶变换)。为了更好的了解这样做的优越性,我们还需要知道单位根的性质
这个不就是定义吗
证明:
\[
w_{2n}^{2k}=cos2k*\frac{2\pi}{2n}+isin2k*\frac{2\pi}{2n}=cosk\frac{2\pi}{n}+isink\frac{2\pi}{n}=w_n^k
\]
证明:
\[
w_n^{k+\frac{1}{2}n}=w_n^k*w_n^{\frac{1}{2}n}=w_n^k*(cos\frac{1}{2}n*\frac{2\pi}{n}+isin\frac{1}{2}n*\frac{2\pi}{n})=w_n^k*(cos\pi+isin\pi)=-w_n^k
\]
前置芝士好长啊
在前置芝士中介绍到了DFT,那么为了配套我们在这里补充这个
这一块内容充分解释了为什么要用单位根来进行代入求值
假设一个\(n-1\)的多项式\(A(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1}\)的DFT为\((y_0,y_1,\cdots,y_{n-1})\)。我们用一种类似于生成函数的方式再构造一个函数\(B(x)=y_0+y_1x+y_2x^2+\cdots+y_{n-1}x^{n-1}\),这时,我们不将单位根带入,取而代之的将他们的相反数(即\(-w_n^0,-w_n^1,\cdots,-w_n^{n-1}\))代入,得到了一组新数记做\((z_n^0,z_n^1,\cdots,z_n^{n-1})\)来化简一波式子
\[
\begin{align}
z_k &= \sum_{i=0}^{n-1}y_i(w_n^{-k})^i\ &= \sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j*(w_n^i)^j)(w_n^{-k})^i\ &= \sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}({w_n^{j-k}})^i)
\end{align}
\]
我们注意到里面的和式是一个等比数列,当\(j=k\)的时候,里面就是\(\sum_{i=0}^{n-1}=n\)。而如果\(j\neq k\)时,根据等比数列的求和公式,这个式子就是酱紫的
\[
\sum_{i=0}^{n-1}({w_n^{j-k}})^i=\frac{(w^{j-k}_n)^n-1}{w^{j-k}_n-1}=\frac{(w^n_n)^{j-k}-1}{w^{j-k}_n-1}=\frac{1-1}{w_n^{j-k}-1}=0
\]
所以上面的式子只有在\(j=k\)的时候的值才是非零的,且为\(n\),我们进一步化简就有
\[
z_k=na_k
\]
即
\[
a_k=\frac{z_k}{n}
\]
这也就为我们在点值表示法和系数表示法之间连接了一座桥梁——我们将单位根代入,可以得到多项式的点值表示;再将单位根的相反数代入由点值表示法得到的点值作为系数的多项式,可以得到这个多项式的系数表示法
至此,我们已经解决了点值和系数的互相转化,它的时间复杂度仍然是将单位根代入求值的复杂度,也就是\(O(n^2)\),仍然不够优秀,有没有更好的方法?
在这里单位根的另一大优越性就体现出来了
对于一个多项式\(A(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^{n-1}\),我们考虑下面的两个新多项式
\[
A_1(x)=a_0+a_2x+a_4x^2+\cdots+a_{n-2}x^{\frac{n}{2}-1}
A_2(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}x^{\frac{n}{2}-1}
\]
那么应该有
\[
A(x)=A_1(x^2)+xA_2(x^2)
\]
对于这个式子,我们将单位根代入,看看会有什么诡异的事情
我们保证\(k<\frac{n}{2}\),先将\(w_n^k\)代入
\[
A(w_n^k)=A_1(w_n^{2k})+w_n^kA_2(w^{2k}_n)
\]
接下来是\(w_n^{k+\frac{n}{2}}\)
\[
\begin{align}
A(w_n^{k+\frac{n}{2}}) &=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}A_2(w^{2k+n}_n)\ &=A_1(w_n^{2k}*w_n^{n})-w_n^kA_2(w^{2k}_n*w^n_n)\ &=A_!(w_n^{2k})-w_n^kA_2(w^{2k}_n)
\end{align}
\]
我们惊奇的发现,这两者之间只是一个符号的差别
这也就是说我们可以将原问题分治成两个子问题——求\(A_1(x)\)与\(A_2(x)\)的点值表示,然后再\(O(n)\)合并
总时间为\(T(n)=2T(\frac{n}{2})+O(n)\),由主定理知为\(O(nlogn)\)
好了最大的瓶颈已经被突破了
黏贴一波代码
#include<iostream>
#include<string>
#include<string.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
using namespace std;
#define rep(i,a,b) for (i=a;i<=b;i++)
typedef long long ll;
#define maxd 1e9+7
#define pi acos(-1.0)
struct complex{
double x,y;
complex(double x1=0.0,double y1=0.0) {x=x1,y=y1;}
};
complex operator +(complex a,complex b)
{
return complex(a.x+b.x,a.y+b.y);
}
complex operator -(complex a,complex b)
{
return complex(a.x-b.x,a.y-b.y);
}
complex operator *(complex a,complex b)
{
return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}
int n,m;
complex a[8000100],b[8000100];
int read()
{
int x=0,f=1;char ch=getchar();
while ((ch<‘0‘) || (ch>‘9‘)) {if (ch==‘-‘) f=-1;ch=getchar();}
while ((ch>=‘0‘) && (ch<=‘9‘)) {x=x*10+(ch-‘0‘);ch=getchar();}
return x*f;
}
void fft(int lim,complex *a,int typ)
{
//cout << lim << endl;
if (lim==1) return;//cout << ‘a‘ << endl;
complex a1[(lim>>1)+10],a2[(lim>>1)+10];int i;
for (i=0;i<=lim;i+=2)
{
a1[i>>1]=a[i];a2[i>>1]=a[i+1];
}
fft(lim>>1,a1,typ);
fft(lim>>1,a2,typ);
complex wn=complex(cos(pi*2.0/lim),sin(pi*2.0/lim)*typ),w=complex(1.0,0.0);
for (i=0;i<(lim>>1);i++,w=w*wn)
{
a[i]=a1[i]+w*a2[i];
a[i+(lim>>1)]=a1[i]-w*a2[i];
}
}
int main()
{
n=read();m=read();int i,lim=1;
for (i=0;i<=n;i++) a[i].x=read();
for (i=0;i<=m;i++) b[i].x=read();
while (lim<=n+m) lim<<=1;
//cout << lim << endl;
fft(lim,a,1);//cout << ‘a‘ << endl;
fft(lim,b,1);
for (i=0;i<=lim;i++) a[i]=a[i]*b[i];
fft(lim,a,-1);
for (i=0;i<=n+m;i++) printf("%d ",(int)(a[i].x/lim+0.5));
return 0;
}
然后你就惊喜的发现了TLE,我们发现luogu的机子足够快让你卡过去了,但时间及其不美观
于是我们考虑优化
所以为什么时间大?元凶很明显就是每一次的递归耗费了大量的时间
于是又有人开始思考了——能不能不用递归?
我们考虑原多项式的系数在递归过程中都被分在了哪个数组里
(借网上一张精美的图)
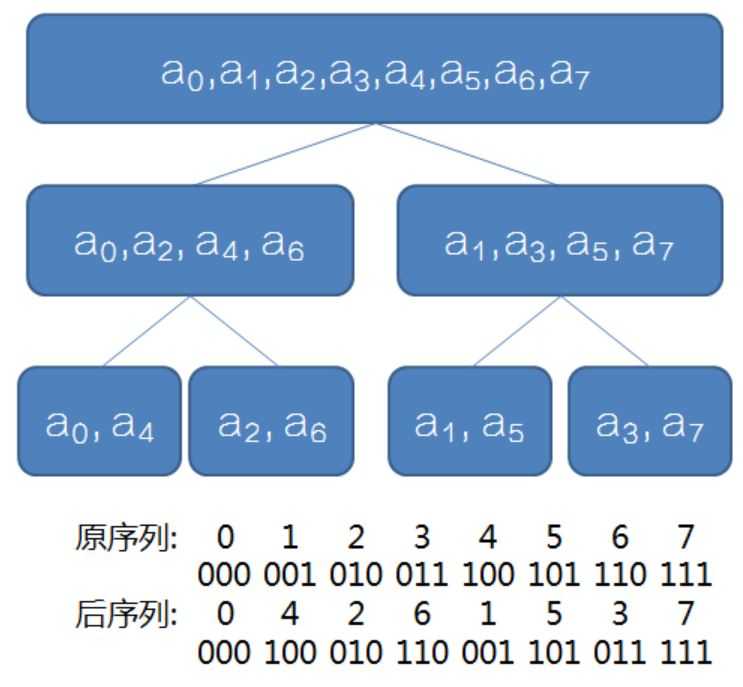
我们发现了原序列与后序列之间每个位置上的数的对应关系就是原序列的数的二进制翻转
证明的话直接考虑每一次分组的话就是根据当前位(从低到高依次考虑每一位)是0还是1,是0的话就分在前一组,是1的话就分在后一组,于是在最后统计的时候就反过来了(从高到低)
我们可以考虑从下面(最底层开始)一层一层的向上合并,最后得到我们想要的结果
于是我们就可以写出下面的有三个循环的嵌套的常数小一点的丑陋的FFT
#include<iostream>
#include<string>
#include<string.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
using namespace std;
#define rep(i,a,b) for (i=a;i<=b;i++)
typedef long long ll;
#define maxd 1e9+7
#define pi acos(-1.0)
struct complex{
double x,y;
complex(double xx=0.0,double yy=0.0) {x=xx;y=yy;}
};
complex operator +(complex a,complex b)
{
return complex(a.x+b.x,a.y+b.y);
}
complex operator -(complex a,complex b)
{
return complex(a.x-b.x,a.y-b.y);
}
complex operator *(complex a,complex b)
{
return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}
complex a[10001000],b[10001000];
int n,m,r[10001000];
int read()
{
int x=0,f=1;char ch=getchar();
while ((ch<‘0‘) || (ch>‘9‘)) {if (ch==‘-‘) f=-1;ch=getchar();}
while ((ch>=‘0‘) && (ch<=‘9‘)) {x=x*10+(ch-‘0‘);ch=getchar();}
return x*f;
}
void fft(int lim,complex *a,int typ)
{
int i,mid;
for (i=0;i<lim;i++)
if (i<r[i]) swap(a[i],a[r[i]]);
for (mid=1;mid<lim;mid<<=1)
{
complex wn=complex(cos(pi/mid),sin(pi/mid)*typ);//也就是w_n^1,方便枚举所有的单位根
int len=mid<<1,sta,j;
for (sta=0;sta<lim;sta+=len)
{
complex w=complex(1,0);
for (j=0;j<mid;j++,w=wn*w)
{
complex x1=a[sta+j],x2=w*a[sta+j+mid];
a[sta+j]=x1+x2;
a[sta+j+mid]=x1-x2;
}
}
}
}
int main()
{
n=read();m=read();int i,lim=1,cnt=0;
for (i=0;i<=n;i++) scanf("%lf",&a[i].x);
for (i=0;i<=m;i++) scanf("%lf",&b[i].x);
while (lim<=n+m) {cnt++;lim<<=1;}
for (i=0;i<=lim;i++)
r[i]=((r[i>>1]>>1)|((i&1)<<(cnt-1)));//处理每一个数的二进制逆序转化,大体思路就是将一个数拆成前n-1位和最后1位然后分别转换
//for (i=0;i<=lim;i++) cout << r[i] << endl;
fft(lim,a,1);
fft(lim,b,1);
for (i=0;i<=lim;i++) a[i]=a[i]*b[i];
fft(lim,a,-1);
for (i=0;i<=n+m;i++)
printf("%d ",(int)(a[i].x/lim+0.5));
return 0;
}好吧FFT是很强大的,在很多组合的题目经常出现
但是它还是有一个缺陷的——多次调用了C++中的三角函数,我们知道这样的话常数巨大且有可能产生精度误差
在某些我们保证了系数均为整数的情况下显得十分多于(这在某些生成函数题中尤为明显)
更重要的是,它并没有对取模这种运算进行很好的兼容
所以又有人才们搞出了一个新东西——NTT
我会在不就之后继续介绍NTT(前提是作业少)
所以想看NTT的话就找我的老师让他少布置点作业吧
完结撒花(雾)
标签:scan 逆序 对应关系 图像 完全 关系 运算 定义 没有
原文地址:https://www.cnblogs.com/zhou2003/p/10212036.html