标签:amp bre root mst 环路 kruskal算法 思路 最小生成树 路径
最小生成树的形成
(1)一个贪心策略设计如下
每个时刻生长最小生成树的一条边,并在整个策略的实施过程中,遵守下述循环不变式的边集合A:
![]()
每一步,选择一条边(u,v)加入集合A,使得A不违反循环不变式。
这样的边使得我们可以“安全地”将之加入到集合A而不会破坏A的循环不变式,因此称之为集合A的“安全边”。

(2)使用的循环不变式方式如下:
初始化:集合A直接满足循环不变式。
保持:算法的循环通过只加入安全边来维持循环不变式。
终止:所有加入到集合A中的边都属于某棵最小生成树,因此,算法第5行所返回的集合A必然是一棵最小生成树。
说明:循环不变式告诉了我们存在一棵生成树,满足![]() 。在进入while循环时,A是T的真子集,因此必然存在一条边
。在进入while循环时,A是T的真子集,因此必然存在一条边![]() ,使得
,使得![]() ,并且(u,v)对于集合A是安全的。
,并且(u,v)对于集合A是安全的。
(3)定义一些概念
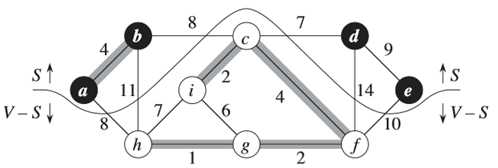
切割:无向图G=(V,E)的一个切割(S,V-S)是集合V的一个划分。
横跨切割:如果一条边(u,v)∈E的一个端点在集合S中,另一个端点在集合V-S中,则称该条边横跨切割(S,V-S)。
尊重集合:如果集合A中不存在横跨该切割的边,则称该切割尊重集合A。
轻量级边:在横跨一个切割的所有边中,权重最小的边称为轻量级边
(4)距离说明上述概念
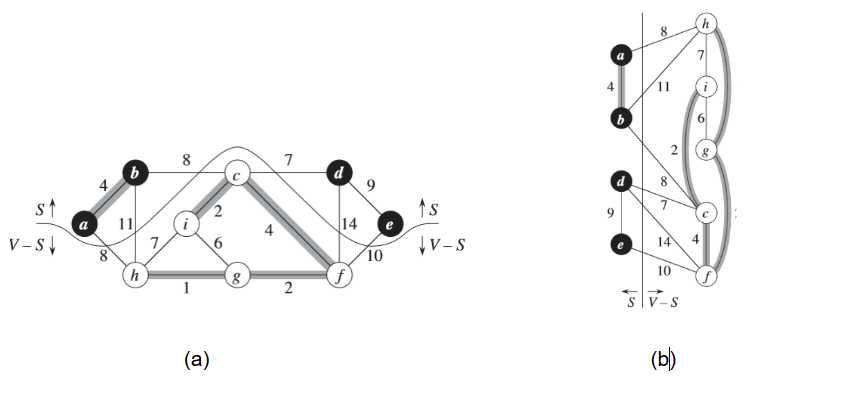
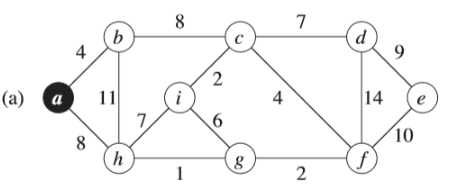
图(a)中所示的黑色结点位于集合S中,白色结点位于V-S中。横跨该切割的边是那些连接白色结点和黑色结点的边。如<a,h><b,c><c,d>等等,其中<d,c>是轻量级边。若定义加了阴影的边属于集合A,那么可以看出集合A中没有横跨切割的边,所以切割<S,V-S>尊重集合A。
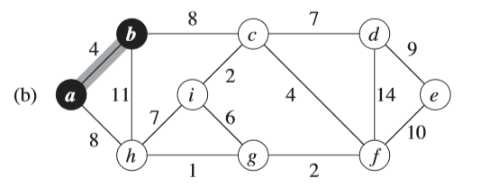
图(b)中是同样一个图,只是换了视角。
(5)辨认安全边的规则
设G=(V,E)是一个在边E上定义了实数值权重函数ω的连通无向图。设集合A为E的一个子集,且A包含在图G的某棵最小生成树中,设(S,V-S)是图G中尊重集合A的任意一个切割,
又设(u,v)是横跨切割(S,V-S)的一条轻量级边。那么边(u,v)对于集合A是安全的。
证明:
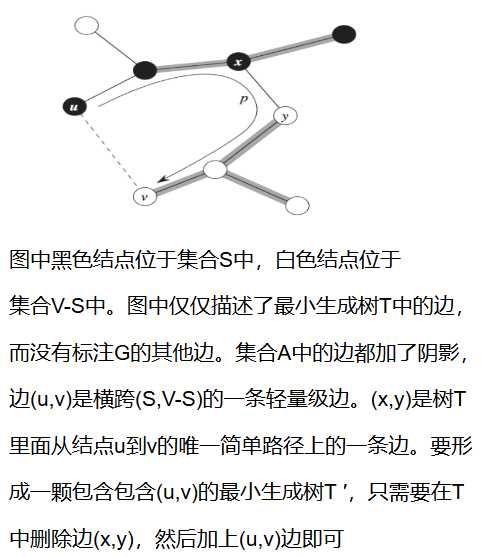
我们现在构建一个最小生成树T ′,通过将A∪{(u,v)}包括在树T ‘中,从而证明(u,v)对集合A来说是安全的。T中包含有G的所有结点,所以(u,v)与T中从结点u到结点v的简单路径p形成一个环。如上图所示。由于结点u,v分别处于切割S,V-S中,T中至少含有一条简单路径p并且横跨该切割。假设(x,y)是这样一条边。由于切割(S,V-S)尊重集合A,所以(x,y)不在集合A中。又因为(x,y)位于T中从u到v的唯一一条简单路径上,将这条边删除会导致T被分为两个连通分量,这时候,将(u,v)加入就能将这两个连通分量连接起来成为一颗心得生成树![]() 。
。
这时候我们来证明T ′是一颗最小生成树。
由于(u,v)是横跨切割的一条轻量级边,并且边(x,y)也横跨该切割,所以我们有ω(u,v)≤ ω(x,y),所以可以简单得出这样一个关系
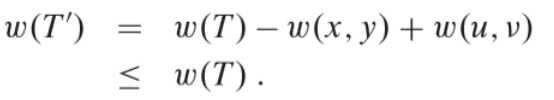
又因为T是一颗最小生成树,ω(T) ≤ ω(T ‘),因此T ′也是一颗最小生成树。
因为 A∈T,且 (x,y)?A,所以A∈T ‘ 。因此![]() 。由于T ‘ 是最小生成树,(u,v)对于集合A而言是安全的。
。由于T ‘ 是最小生成树,(u,v)对于集合A而言是安全的。
在算法GENERIC-MST推进的过程中,集合A始终保持无环状态( 每条边都是安全的 )。算法执行的任意时刻,图G A =(V,A)是一个森林。
while循环执行|V|-1次,每次找出构造最小生成树所需的一条边。每遍循环将树的数量减少1。当整个森林只含有一棵树时,算法终止。
Kruskal算法
Kruskal和Prim算法是求解最小生成树的两个经典算法。它们都是GENERIC-MST算法的具体细化:
(1)Kruskal算法找安全边的方法:在所有连接森林中两棵不同树的边中,找权重最小的边(u,v)。设C 1 和C 2 为边(u,v)所连接的两棵树。边(u,v)是C 1 的一条安全边。

(2)简单讲述一下Kruskal算法的工作过程。算法的1~3行将集合A初始化为一个空集,并创建|V|棵树,每棵树仅包含一个结点,作为初始情况。5~8行中的for循环按照权重从低到高的次序对每一条边逐一进行检查。对于每条边(u,v)而言,循环将检查该结点u和结点v是否属于同一棵树。如果是,这条边不能加入,避免形成环路。如果不是,则两个端点分别属于不同的树,算法第7行将吧这些边加入到集合A中,第8行将两棵树进行合并。
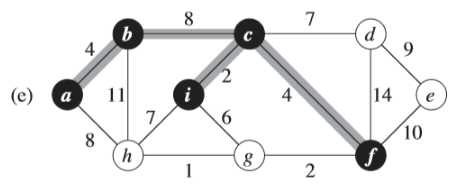
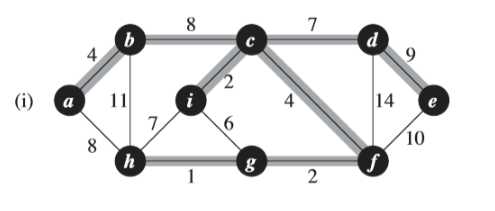
(3)下面给出一个具体的例子看看算法的流程
①首先找到最小权重的边为<h,g> = 1
②继续寻找下一条权重次小的边,以此类推
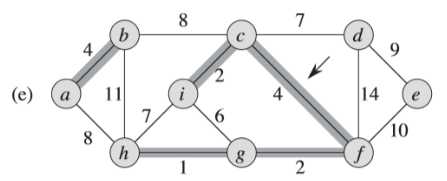
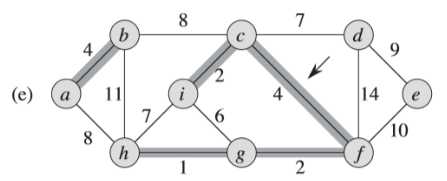
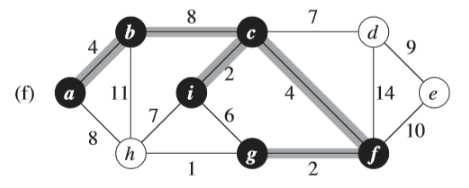
③注意到,(f)图中此时权重为6的边的两个端点i和g都属于同一棵树(<i,c,f,g,h>)中,所以不能加这条边加入,否则会形成环路
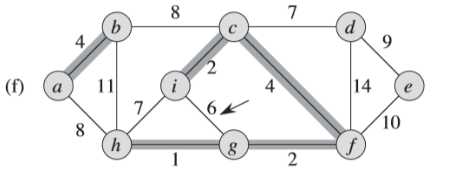
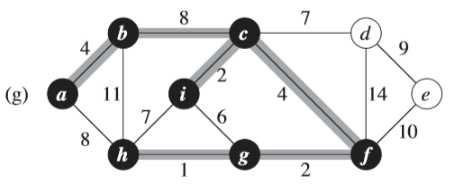
④同③一样,(h)图中的权重为7的边不同加入集合中,避免形成环路(<i,c,f,g,h>)
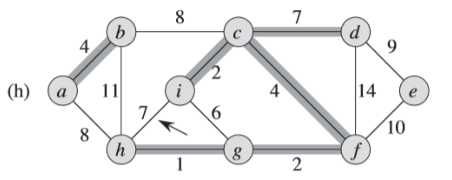
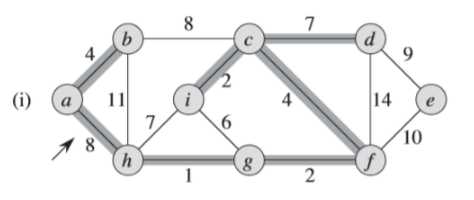
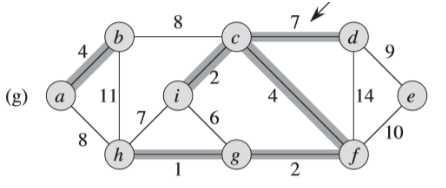
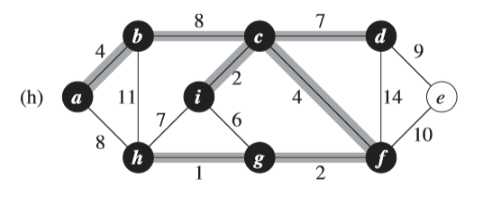
⑤同④一样,(j)图中的权重为8的边不同加入集合中,避免形成环路(<a,b,d,c,f,g,h>)
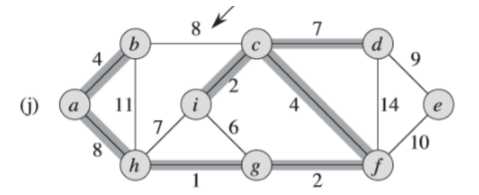
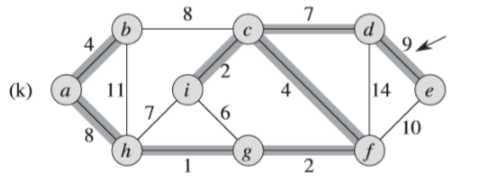
⑥同理,<e,f>边如果加入集合中,会形成环路<c,d,e,f>;<b,h>不能加入集合中,会形成<a,b,h>环路;<d,f>不能加入集合中,会形成<c,f,d>环路

1 package cn.Graph; 2 3 import java.util.ArrayList; 4 import java.util.Scanner; 5 6 /** 7 * 使用kruskal算法生成图的MST 8 * 其中: 9 * 1.图的顶点存在了数组中 10 * 2.图的带权边使用了EdgeNode对象,存在了数组中 11 * 3.边按照权重进行排序利用最小堆进行排序,每次取出最小堆的根节点,便是权最小的边 12 * 4.每次向MST中添加边肯定添加最小权的边,唯一条件便是不构成环 13 * 5.上述不构成环是利用等价类<并查集>实现的 14 * 6.并查集实现:树!每个顶点两个域:parent域&root域!find-union!重量规则! 15 * @author cy 16 * 17 */ 18 public class Kruskal { 19 boolean[] root; 20 int[] parent; 21 int currentSize=0; 22 int maxSize=0; 23 EdgeNode[] minHeap=new EdgeNode[20]; 24 25 /** 26 * 初始化每个顶点为一个类 27 * @param verNum 顶点的数量 28 */ 29 public void initialize(int verNum){ 30 root=new boolean[verNum+1]; 31 parent=new int[verNum+1]; 32 33 for(int vertex=1;vertex<=verNum;vertex++){ 34 parent[vertex]=1; 35 root[vertex]=true; 36 } 37 } 38 39 /** 40 * 寻找某个顶点元素所在的类 41 * @param vertex 顶点 42 * @return 返回的是顶点所在的类 43 */ 44 public int find(int vertex){ 45 while(!root[vertex]){ 46 vertex=parent[vertex]; 47 } 48 return vertex; 49 } 50 51 /** 52 * 利用重量规则将两个根节点为i,j的类合并 53 * @param i 根节点为i 54 * @param j 根节点为j 55 */ 56 public void union(int i,int j){ 57 if(parent[i]<parent[j]){ 58 parent[j]+=parent[i]; 59 root[i]=false; 60 parent[i]=j; 61 }else{ 62 parent[i]+=parent[j]; 63 root[j]=false; 64 parent[j]=i; 65 } 66 } 67 68 /** 69 * 通过weight构建以EdgeNode为节点的最小堆 70 * @param edgeNode为带权的边集 71 */ 72 public void createMinHeap(EdgeNode[] edgeNode){ 73 currentSize=edgeNode.length; 74 maxSize=minHeap.length; 75 if(currentSize>=maxSize){ 76 maxSize*=2; 77 minHeap=new EdgeNode[maxSize]; 78 } 79 for(int i=0;i<currentSize;i++) 80 minHeap[i+1]=edgeNode[i]; 81 82 int y,c; 83 for(int i=currentSize/2;i>=1;i--){ 84 EdgeNode node=minHeap[i]; 85 y=node.weight; 86 c=2*i; 87 while(c<currentSize){ 88 if(c<=currentSize && minHeap[c].weight>minHeap[c+1].weight) 89 c++; 90 if(minHeap[c].weight>=y) 91 break; 92 minHeap[c/2]=minHeap[c]; 93 c=c*2; 94 } 95 minHeap[c/2]=node; 96 } 97 } 98 99 /** 100 * 最小堆删除两种思路,一种和前面一样,就是一直跟踪放在根节点的那个最后一个节点最终插入的位置 101 * 另一种思路便是每一次完成完整的交换然后下一一层在进行同样处理 102 */ 103 public EdgeNode deleteMinHeap(){ 104 if(currentSize<1) 105 System.out.println("堆已经为空!无法执行删除"); 106 EdgeNode node=minHeap[1]; 107 minHeap[1]=minHeap[currentSize]; 108 currentSize-=1; 109 110 int c=2,j=1; 111 EdgeNode node1=minHeap[currentSize+1]; 112 while(c<=currentSize){ 113 if(c<currentSize && minHeap[c].weight>minHeap[c+1].weight) 114 c++; 115 if(node1.weight<=minHeap[c].weight) 116 break; 117 minHeap[j]=minHeap[c]; 118 j=c; 119 c=c*2; 120 } 121 minHeap[j]=node1; 122 return node; 123 } 124 125 /** 126 * 根据图的顶点集合带权边集生成MST 127 * @param verArray 顶点集 128 * @param edgeNode 带权边集 129 */ 130 public void minSpanningTree(int[] verArray,EdgeNode[] edgeNode){ 131 ArrayList<EdgeNode> nodeList=new ArrayList<EdgeNode>(); 132 133 initialize(verArray.length); 134 createMinHeap(edgeNode); 135 136 for(int i=1;i<=currentSize;i++){ 137 System.out.println(minHeap[i].u+" "+minHeap[i].v+" "+minHeap[i].weight); 138 } 139 140 for(int i=0;i<edgeNode.length;i++){ 141 EdgeNode node=deleteMinHeap(); 142 int jRoot=find(node.u); 143 int kRoot=find(node.v); 144 if(jRoot!=kRoot){ 145 nodeList.add(node); 146 union(jRoot,kRoot); 147 } 148 } 149 System.out.println("使用Kruskal算法得到图的最小生成树为:"); 150 for(int i=0;i<nodeList.size();i++){ 151 System.out.println(nodeList.get(i).u+" "+nodeList.get(i).v+" "+nodeList.get(i).weight); 152 } 153 } 154 155 public static void main(String[] args) { 156 System.out.println("请输出图的顶点数和边数:"); 157 @SuppressWarnings("resource") 158 Scanner scan=new Scanner(System.in); 159 int verNum=scan.nextInt(); 160 int edgeNum=scan.nextInt(); 161 162 int[] verArray=new int[verNum]; 163 System.out.println("请依次输入顶点:"); 164 for(int i=0;i<verNum;i++){ 165 int vertex=scan.nextInt(); 166 verArray[i]=vertex; 167 } 168 169 EdgeNode[] edgeNode=new EdgeNode[edgeNum]; 170 System.out.println("请依次输入边的顶点和权重:"); 171 for(int i=0;i<edgeNum;i++){ 172 int u=scan.nextInt(); 173 int v=scan.nextInt(); 174 int weight=scan.nextInt(); 175 EdgeNode node=new EdgeNode(); 176 node.u=u; 177 node.v=v; 178 node.weight=weight; 179 edgeNode[i]=node; 180 } 181 Kruskal kruskal=new Kruskal(); 182 kruskal.minSpanningTree(verArray,edgeNode); 183 } 184 } 185 class EdgeNode { 186 int weight; 187 int u,v; 188 }
Prim算法
(1)Prim算法的每一步是在连接集合A和A之外的结点的所有边中,选择一条轻量级边加入到A中。所加入的边对于A也是安全的。Prim算法的基本性质:集合A中的边总是构成一棵树。
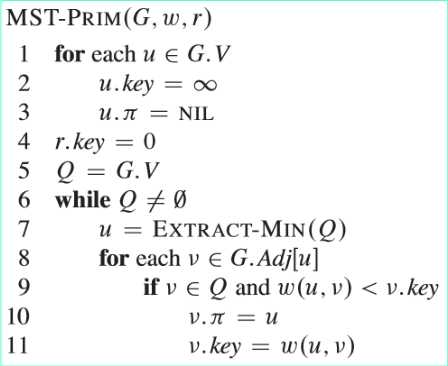
(2)简单描述一下上述算法的流程。1~5行将每个节点的key值设置为∞(除根节点r以外,根节点key值置为0,作为第一个被处理的点),然后将每个结点的父节点置为NIL,并对最小优先队列Q进行初始化,使其包含图中的所有节点。
算法维持的循环不变式由3个部分组成:
①A={(v,v.π):v∈V-{r}-Q}
②已经加入到最小生成树中的结点集合为V-Q
③对于所有结点v∈Q,如果v.π≠NIL,则v.key<∞并且v.key是连接结点v和最小生成树中某个节点的轻量级边(v,v.π)的权重
第7行找出结点v∈Q,该结点是某条横跨切割<V-Q,Q>的轻量级边的一个端点,然后将结点u从队列中删除,并将其加入到集合V-Q中,也就是将边<u,u.π>加入到集合A中。8~11行的for循环将每个与u邻接但是不在树中的结点v的key和π属性进行更新,从而维持循环不变式。
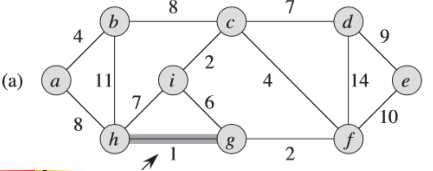
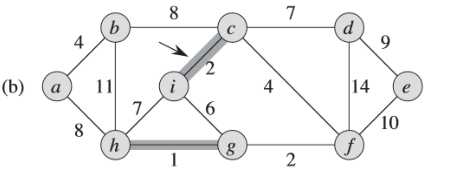
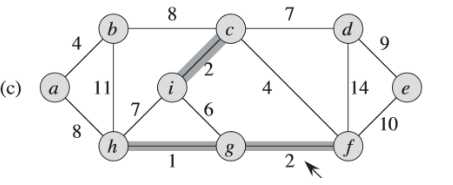
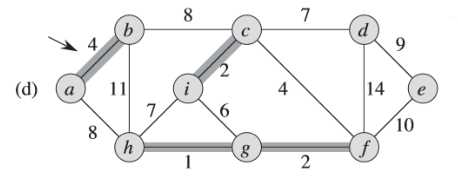
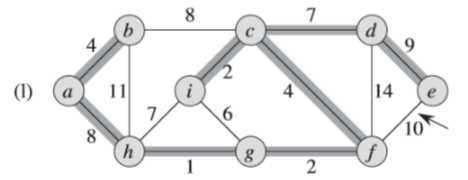
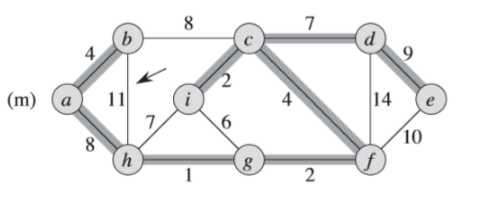
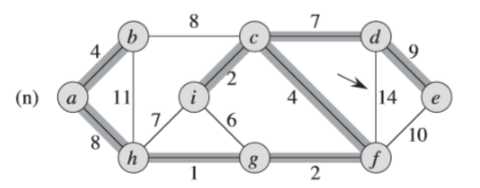
(3)简单看一个Prim算法的例子
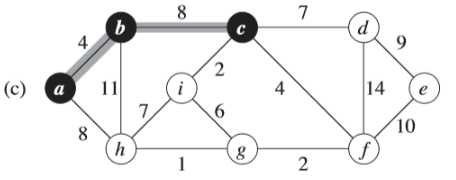
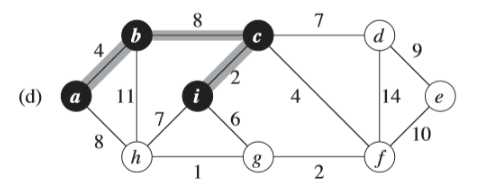
例子中,初始的根节点为a,加阴影的边和黑色结点属于树A。在算法的每一步,树中的结点就决定了图的一个切割,横跨该切割的一条轻量级边就被加入到树中。
例如:在图(b),轻量级边有两条,<b,c>,<a,h>的权重都为8,所以可以选择两条边中的一条加入到树中
标签:amp bre root mst 环路 kruskal算法 思路 最小生成树 路径
原文地址:https://www.cnblogs.com/fsmly/p/10215179.html