标签:之间 测试 ima 百度 最长回文字串 nbsp 最大字串 子串 tin
百度了好长时间,看了很多篇博客才稍微看懂,所以自己写篇博客加深一下映像,并且写的尽量详细一些 希望大家能够只这篇博客就能看懂,能少走些弯路
1.添加特殊字符
通常情况下,对于一个字符串,需要求解其最长子串时,我们通常需要考虑其字符长度的奇偶性问题,比如‘aba‘与‘abba‘的求解方式不太一样,但是马拉松算法在每个字符之间都添加了一个特殊字符(原字符串所没有的),比如‘#‘或‘$‘符号,比如‘aba‘==>‘#a#b#a#‘,‘abba‘==>‘#a#b#b#a#‘,那么此时,无论之前字符长度是否为奇偶,现在都变成了奇数,此时我们只需要考虑这一种情况就可以了
为什么插入特殊字符后,字符串都变为奇数个字符了?
偶数情况: 假设我们有一个偶数个字符的字符串,我们令其字符数为a,此时我们为其插入特殊字符,特殊字符数为(两边各一个+中间插入a-1个) 即有: 插入后字符个数 = a+(a-1+2) =2a+1==> 因2a为偶数所以2a+1为奇数 奇数情况: 假设我们有一个奇数个字符的字符串,我们令其字符数为a+1,其a为偶数,此时我们插入特殊字符数为(两边各一个+中间插入a个) 即有: 插入后字符数=a+1+a+2 =2a+3==>2a为偶数所以2a+3为奇数
如果我们令每一个字符都与自己构成回文数,并且记录其回文半径(以当前字符为中心,向两边扩散,如果字符对称则半径+1,直到出现不对称字符),比如单个字符‘a‘变为新字符串‘#a#‘,新字符串的回文半径将为[1,2,1],此时我们可以写一下代码
1 public static void test(String str) { 2 3 /* 向字符串插入特殊字符 */ 4 List<Character> strs=new ArrayList<>(); 5 6 strs.add(‘#‘); 7 for (int i = 0; i < str.length(); i++) { 8 strs.add(str.charAt(i)); 9 strs.add(‘#‘); 10 } 11 12 /* 存储每位字符的最大回文半径 */ 13 int[] len=new int[strs.size()]; 14 /* 最大回文字串的中心位置 */ 15 int id=0; 16 17 /* 遍历新字符串 */ 18 for (int i = 0; i < strs.size(); i++) { 19 20 while(i-len[i]>=0&&i+len[i]<strs.size()&&strs.get(i-len[i])==strs.get(i+len[i])) { 21 len[i]++; 22 } 23 24 /* 如果新查找串更长 则替换最长回文字串的中心位置 */ 25 if(len[i]>len[id]) { 26 id=i; 27 } 28 } 29 30 for (int i = id-(len[id]-1); i <= id+(len[id]-1); i++) { 31 System.out.print(strs.get(i)); 32 } 33 }
测试一下
public static void main(String[] args) { test("123242329"); }
结果: #2#3#2#4#2#3#2#
此时我们已经能获取到最长字串了,当然这还远远不能算是马拉松算法,见图片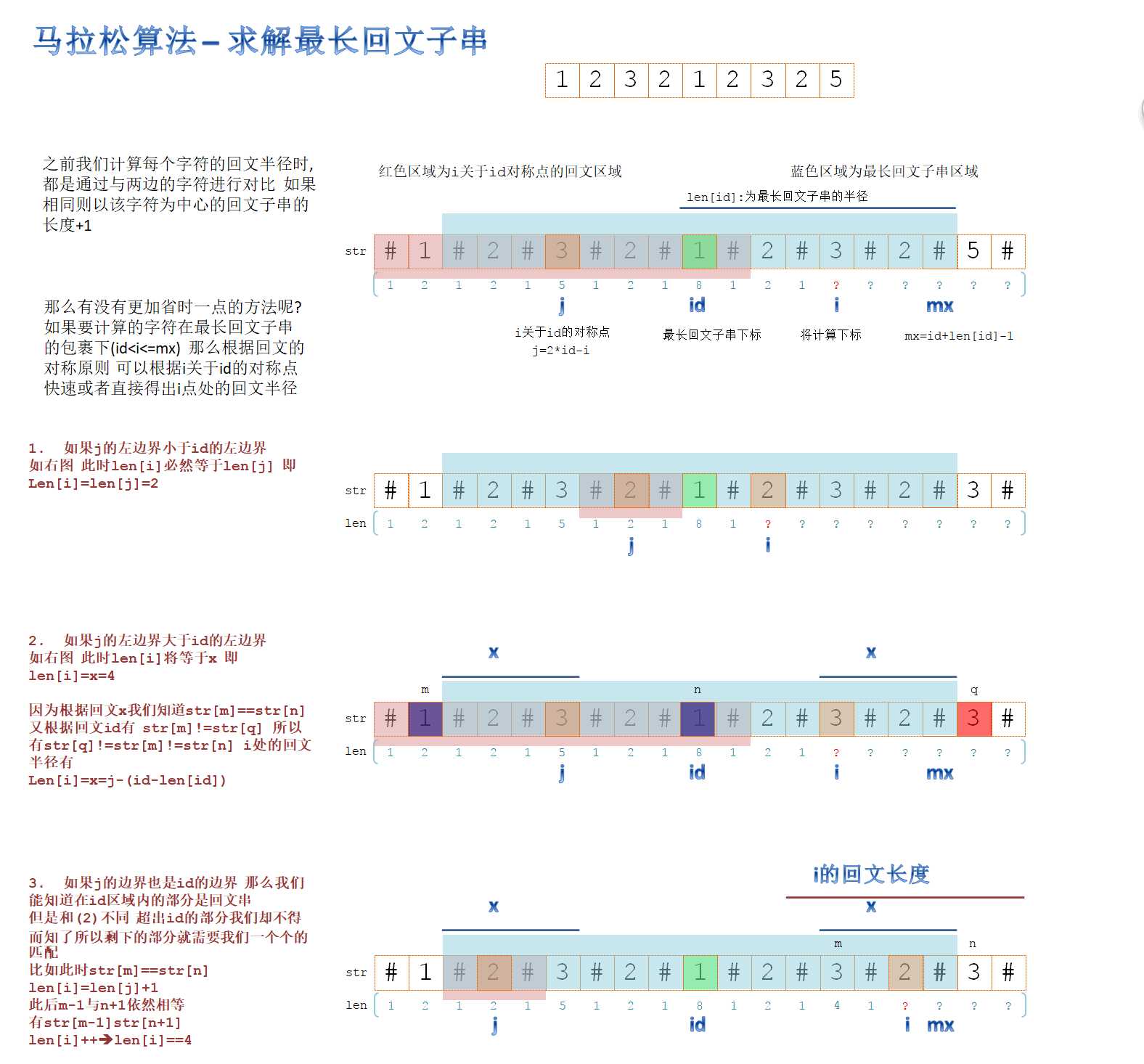
代码
1 public static void manacher(String str) { 2 3 /* 向字符串插入特殊字符 */ 4 List<Character> strs=new ArrayList<>(); 5 6 strs.add(‘#‘); 7 for (int i = 0; i < str.length(); i++) { 8 strs.add(str.charAt(i)); 9 strs.add(‘#‘); 10 } 11 12 /* 存储每位字符的最大回文半径 */ 13 int[] len=new int[strs.size()]; 14 /* 最大回文字串的中心位置 */ 15 int id=0; 16 /* 最大回文字串的右边界 */ 17 int mxindex=0; 18 19 /* 遍历新字符串 */ 20 for (int i = 0; i < strs.size(); i++) { 21 /* 如果 i在最大回文串中 则可以进行一些判断 */ 22 if(i<mxindex) { 23 /* 判断i点关于最大字串中心对称点j的回文半径长度 */ 24 int j=2*id-i; 25 26 /** 27 * 当字符串 "# 1 # 2 # 3 # 2 # 4 # 2 # [3] # 2 # 9 #" 28 * 运行到3位置时,其左边字符必定全部计算过回文数了 29 * 此时最大的回文串为 "# 1 # 2 # 3 # 2 # $4$ # 2 # [3] # 2 #" 30 * 右3包含与其中 并且位于中心字符$4$的右边 31 * 此时根据对称原则找到3的对称点\332 * "# 1 # 2 # \3\ # 2 # $4$ # 2 # [3] # 2 #" 33 * 此时的对称点\3\必然已经计算过了,而其回文半径有一下几种情况 34 * 1. 对称点\3\的回文半径在在最长回文之内 根据对称原则 此时计算点回文半径必然也为此值 35 * 2. 对称点\3\的回文半径超过了最长回文字符,此时计算点回文半径应为对称点\3\到左边界的长度 36 * 3. 对称点\3\的回文半径刚好在最长回文边界处 此时计算点的回文半径为[对称点回文半径+继续暴力求解] 37 * 38 *///1.2.两种情况都不会为最长回文子串 所以只需要设置其回文半径就可以 39 if(len[j]<mxindex-i) { 40 len[i]=len[j]; 41 continue ; 42 }else if(len[j]>mxindex-i) { 43 len[i]=mxindex-i; 44 continue ; 45 }else if(len[j]==mxindex-i) { 46 len[i]=len[j]; 47 } 48 } 49 50 51 while(i-len[i]>=0&&i+len[i]<strs.size()&&strs.get(i-len[i])==strs.get(i+len[i])) { 52 len[i]++; 53 } 54 55 /* 如果新查找串更长 则替换最长回文字串的中心位置 */ 56 if(len[i]>len[id]) { 57 mxindex=i+len[i]-1; 58 id=i; 59 } 60 } 61 62 for (int i = id-(len[id]-1); i <= id+(len[id]-1); i++) { 63 System.out.print(strs.get(i)); 64 } 65 } 66
如果有地方写的错误,或者有什么疑问与建议,欢迎大家提出来 愿与大家一同进步
标签:之间 测试 ima 百度 最长回文字串 nbsp 最大字串 子串 tin
原文地址:https://www.cnblogs.com/wangbingc/p/10217139.html