标签:培训 结构 分辨率 情况 假设 关心 图片 缺点 训练
基于递阶递归神经网络的音频超分辨率
作者:Berthy Feng
摘要
本工作提出了一种用于音频超分辨率的递归模型,该模型的任务是推断低分辨率录音的高分辨率版本。鉴于缺乏基线方法和最合适的深度学习方法的模糊性,我们将重点放在递归神经网络上。我们提出了一种分层递归神经网络(Hrnn),它使用基于回归的损失和感知损失相结合的损失函数进行训练。在本文中,我们提出了基线hrnn的体系结构,以及改进基线的两种感知损失。我们的基线模型优于插值方法,通过提供可解释性和产生感知现实结果,我们提出的感知损失在基线上得到了改善。
一、引言
1.1 音频超分辨率
音频超分辨率的任务是提高音频记录的分辨率.有各种方法来概念化这个任务,无论是在时域还是在频域。
在时域上,任务是提高给定音频波形的采样率。例如,在16 kHz采样的音频的分辨率是在8 kHz时采样的音频的两倍。较高的采样率每个时间单位捕获更多的样本,从而捕获更高频率的声音成分,其中可能包括浊音的泛音和房间的混响。在频域中,任务是扩大音频信号的带宽。也称为带宽扩展,目标是从给定的窄带信号产生宽带信号,其中宽带输出具有恢复较高频带频率的能量。
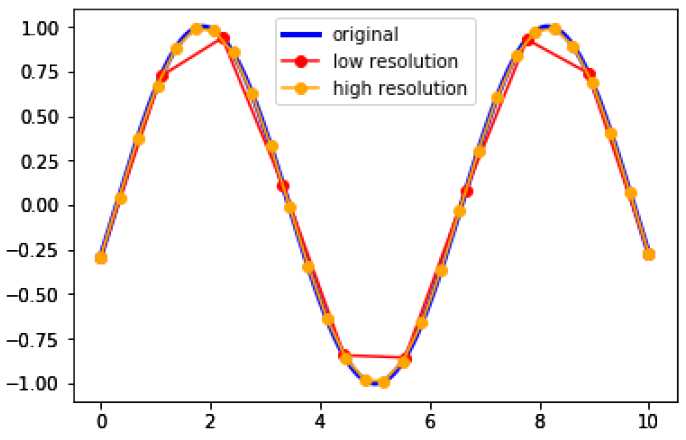
图1:采样率对波形分辨率影响的可视化。橙色线采样原始正弦波的频率是红线的三倍,从而得到更准确的波形。我们的任务是推断出仅给出红线的橙色线。
关于音频超分辨率的两种思维方式都是有效的,因为它们都旨在恢复高频分量。然而,它们往往导致不同的结果。时域方法将音频建模为时间序列,从而更准确地再现信号的波形和相位信息。频域方法将音频建模为频率频谱,从而更准确地再现每个频率上的能量和音频的“颜色”。换句话说,时域方法可能会导致更真实的波形,而频域方法可能会导致更真实的谱图。目前,大多数最先进的音频合成方法都是在频域工作的,使用的是前馈网络,而不是反复出现的网络。
1.2 我们的工作
我们的方法是在时域,因为所提出的结构工作在波形水平。为了提高频域的准确性,我们提出了一种感知损失,以鼓励真实感谱图的结果。我们的任务特别是单扬声器语音的超分辨率,其中输入是一个8千赫的语音记录,输出是16千赫的版本,恢复了更高的频带频率。
单说话人的原因是很难建立一个代表所有人类声音的模型,因为一个声音的特征是它的音色。将采样率提高到16 kHz的原因是为了给录音增加一种存在感。许多带宽扩展技术的目标是从很低的采样率(如3 kHz)到中等采样率(例如8 kHz)。达到8 kHz将恢复基本的语音质量,并且在许多电信应用中都很有用,从而使传输语音具有可分辨性。然而,超过8千赫的频率增加了更微妙的分辨率和颜色,给听众一个更清晰的画面房间和扬声器。
考虑到音频波形的时序性,我们实验了一种用于音频超分辨率的递归模型.我们将注意力集中在递阶递归神经网络上,它能够在多个时间尺度上对序列信息进行建模。
1.3 递归神经网络
递归神经网络(RNN)是具有反馈连接的神经网络[15]。在给定的时间步骤t中,rnn有一个隐藏状态ht,它是根据先前的隐藏状态ht??1和特定于该时间步骤的输入xt的函数计算的。这个重复公式表示为:
$$h_t=f_W(h_{t-1},x_t)$$
函数fw具有参数sw,一旦学会,就会在所有时间步骤中保持不变。
Rnns模型的时序数据非常好。它们广泛应用于与自然语言处理相关的任务中,包括机器翻译、图像字幕和文本生成。自从20世纪90年代流行起来[15]以来,出现了各种类型的rnn,包括长时记忆(Lstm)网络[4]和门控递归单元(Gru)[1]。
1.4 层次递归神经网络
音频的连续性使其成为一种循环模型。然而,一个RNN可能不足以捕获重建高分辨率信号所需的信息。音频包含低级信息,如精确的采样值,以及高级信息,如语音音素、回声和混响。层次RNN(hrnns)提供了一种在多个层次上使用信息的方法。
hrnn包含多个rnn层,每个层的输入覆盖不同的范围。samplernn是一种最先进的音频生成方法,其体系结构为hrnn[12]。例如,具有三层的样本,可能一次具有最高层的rnn处理八个样本,中间层rnn一次处理两个样本,而低层rnn一次处理一个样本。在hrnn中,较低层rnns通常将较高层rnn输出作为附加输入。在此层次结构中安排rnn允许模型从多个级别的信息中学习。这种方法在音频中特别有用,因为在音频中有一个记录语音特征的层次结构。
1.5 概括
在第二节中,我们描述了我们工作的动机,包括音频超分辨率的应用,以及我们使用反复模型和知觉损失的想法背后的灵感。在第三节中,我们阐述了项目的两个主要和相互关联的目标。在第四节中,我们回顾了带宽扩展和音频生成方面的相关工作。在第五节中,我们解释了所提出的hrnn体系结构和两种类型的知觉损失。在第六节中,我们描述了我们的实施和培训方法。在第7节中,我们展示了我们的结果,并证明了我们提出的方法实现了感知现实的输出。在第8节和第9节中,我们为未来的工作提供结论和指导。
2.1 音频超分辨率应用
传统上,音频超分辨率被称为带宽扩展.这项任务在电信领域有着重要的应用,在那里,提高低带宽设备上的语音质量是很重要的。音频超分辨率也有更现代的应用。它在文本到语音合成中很有用,在这种情况下,语音可以首先在低分辨率的情况下合成.它也是有用的人谁希望改善他们的录音质量,因为音频最初记录在一个低质量的麦克风或因为音频被压缩到一个较低的采样率。由于我们的工作集中在8千赫以上的高频段,我们的目标是给一种在场感的演讲录音。我们假设窄带语音已经是智能的。
2.2 理解RNN的建模能力
WaveNET[17]是一种用于音频生成的前馈网络,它的成功促使许多研究人员默认使用前馈网络来执行音频合成任务。然而,一种基于时间的、反复出现的音频超分辨率方法的可能性还有待于充分探讨.需要用rnns来进行超分辨率的实验,这是这项工作的动机之一。
2.3 来自机器视觉的启发
计算机视觉中的许多思想都可以转换成音频。对于图像的超分辨率,已经提出了多种最先进的方法,因此,从图像超分辨率中获得洞察力可以帮助我们在音频领域。具体来说,增加知觉损失对图像的超分辨率有很大的帮助.感知丢失的关键思想是鼓励感知真实的结果,而音频超分辨率的目的也是为了产生感知真实的结果(例如相移等变换不会影响人耳感知的质量,所以我们不关心与地面真相完全匹配的问题)。考虑到感知损失这一有前途的想法,可能有可能克服RNN的典型缺点,例如过度平滑。因此,另一个动机是利用计算机视觉中的洞察力,并将它们应用于音频问题。
3、 目标
本项目的目的是开发一种用于音频超分辨率的分级递归神经网络。具体来说,这意味着完成这两个步骤:
1。提出了一种基线hrnn方法,对单个说话人的语音达到可接受的效果。
2.提出了一种感知损失改进的基线方法。更普遍的目标是找出基于RNN的音频超分辨率方法的优缺点,并为今后的工作提出方向。
4、有关工作
4.1 基于学习的声码器方法
声码器是一种常用的音频域建模方法。在该方法中,提取窄带输入信号的频谱参数,并将其映射到相应的宽带输出信号的频谱特征。已有许多经典的机器学习方法,包括码本映射、高斯混合模型和隐马尔可夫模型.神经网络也被用来编码输入特征并对其进行解码以产生宽带输出。为此提出了稠密神经网络[10]和递归神经网络[3]。尽管声码器的参数化,但这些方法的难点是恢复相位谱,同时保持原始的语音质量。
4.2 生成音频模型
由于WaveNet[17]及其后续产品Tacotron 2[14]的成功,基于波形的音频生成方法变得越来越流行。两种方法都使用扩张卷积来扩展卷积神经网络(CNN)的接收场,并且都是完全前馈的。塔克龙2是以梅尔光谱图预测为条件的,这一想法影响了我们的设计。基于光谱图的知觉损失。Wavenet和Tacotron 2用于随机音频生成和文本到语音合成,这两个问题都需要从头开始模拟音频分布。但是,这些方法并没有针对超分辨率任务进行优化,因此在培训期间可以进行更多的监督。虽然这些前馈网络实现了最先进的综合,我们的目标是提出一个替代,循环网络,专门在超分辨率。
Samplernn[12]是主要的循环生成模型,也是我们建议的建筑灵感。然而,由于采样的目的是从零开始对音频的分布进行建模,并且允许输出的随机性,所以它并没有为超分辨率进行优化。然而,超分辨率取决于输入信号,因此任务允许更有限的输出空间和有监督的训练方案。
4.3 深度学习的方法
直到最近,研究人员才专门为音频超分辨率设计了深度学习模型。库拉肖夫等人。提出了一种简单的卷积神经网络作为音频超分辨率的基线神经网络[8]。玲等人将samplernn应用于带宽扩展,并获得比完全前馈网络更好的结果[11]。这两项工作都提供了相当简单的模型,并提出了改进的机会。林等人的工作。为我们的方法提供了灵感,尽管我们修改和改进了它们的模型,使其更适合于音频的超分辨率。
5、方法
5.1 hrnn体系结构
一般情况下,分层递归神经网络总体上可能有k层,其中顶层k??1层在帧级(其中帧是样本序列)上工作,底层一次处理一个样本。我们提出了一个三层递归神经网络作为基线模型,它包括两个帧层和一个样本层。
输入。窄带输入在8 kHz采样,然后上采样到16 kHz,使其与宽带16 kHz输出具有相同的采样长度。注意,即使输入包含每秒16000个样本,其频率内容仍然不超过8 kHz。然后使用Mu-law编码将每个样本量化为0到255之间的值。这允许我们使每个输入样本成为长度256的一个热编码向量,其中对应于样本量化值的索引被标记为“1”,所有其他索引都标记为“0”。设fx1;:;xtg表示长度t的整个输入序列(例如,对于在16 kHz采样的三秒音频,t=48000)。每个xt表示一个热向量,表示样本在t处的量化值。
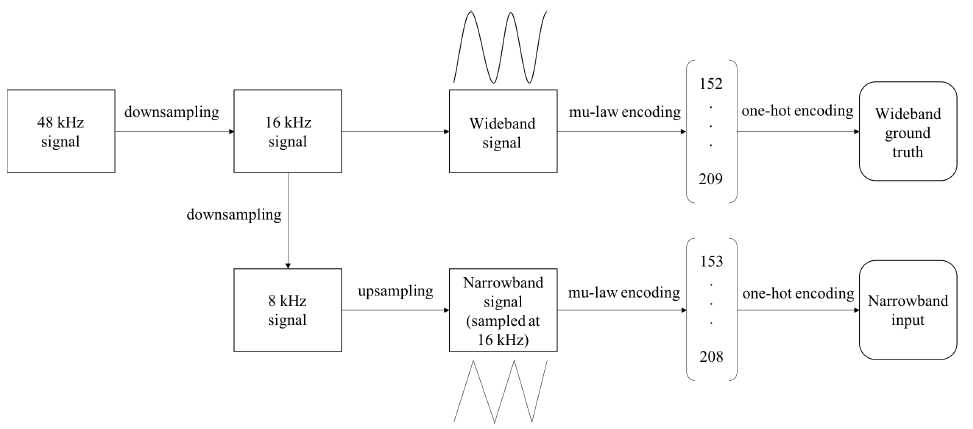
图三 准备输入
第三层。最高帧层一次处理8个样本。我们将其实现为单层RNN(尽管可以添加任意数量的层)。在t时,它的输入是:
$$f_t^3={x_t,...,x_{t+7}}$$
RNN的隐藏状态表示为:
$$h_t^3=g^3(h_t-1^3,g_t^3)$$
其中ht??1是以前的隐藏状态,g3是学习的rnn函数。
为了将信息传递到下一层,顶层为第2层生成条件向量。由于第二层每次处理两个样本,第三层一次处理八个样本,第三层在每一时间步骤输出四个条件向量(它处理的每两个样本中就有一个)。时间t处的条件向量表示为:
$$d_{t+j}^3=W_j^3h_t^3,j=0,2,4,6$$
所有d3tj都成为第2层的输入。
在第三层中,我们为每一个新的时间步骤增加8个样本。这是因为我们希望第3层的每个时间步骤都有不重叠的输入序列。
第二级。中间层一次处理两个样本。也是作为单层RNN实现的,它在时间t处的输入是样本输入和第3层的条件向量的线性组合:
$$f_t^2={x_t,x_{t+1}}+{d_t^3}$$
其隐藏状态表示为:
$$h_t^2=g^2(h_{t-1}^2,f_t^2)$$
第2级还为每个样本输出一个条件向量,然后将其用作第1层的输入。在每个时间步骤t中,RNN输出两个条件向量:
$$d_{t+j}^3=W_j^3h_t^3,j=0,1$$
在第二层中,我们为每一个新的时间步骤增加两个样本,这样输入序列是不重叠的。
第1级最低层,也称为样本层,是一个完全前馈多层感知器(MLP).我们将其实现为三个完全连接的层。在此阶段,输入样本被发送到一个学习的256维嵌入层,因此每个输入样本XT被嵌入为实值的256维向量ET。输入(表示为i1)是嵌入向量f1=[E1;:;ET]和条件向量D2=[D21;:;D2 t]:
$$i^1=W^1f^1+d^2$$
对于每个输入样本XT,MLP在输入信号的窄带版本中预测相应的输出样本yt(注意yt是标量)。总之,我们描述了用hrnn建模的函数背后的体系结构:
$$y_t=HRNN(x_t),\forall t\in T$$
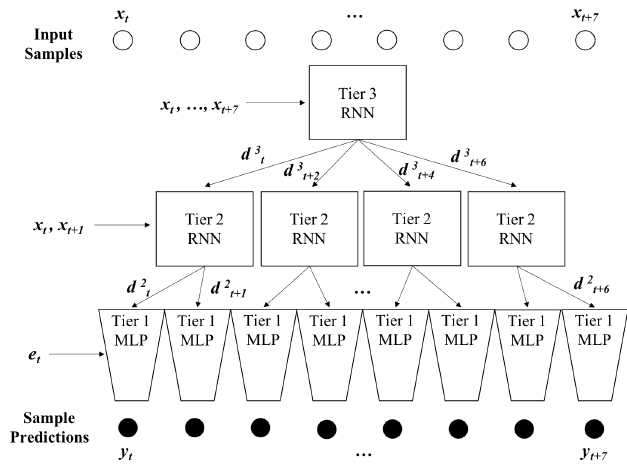
图4 HRNN 建筑学
Hierarchical Recurrent Neural Networks for Audio Super-Resolution
标签:培训 结构 分辨率 情况 假设 关心 图片 缺点 训练
原文地址:https://www.cnblogs.com/LXP-Never/p/10228643.html