『算法学习』轻量级网络MobileNet_v2

标签：输入   说明   time   网络   ima   公式   实验   情况   spl   

前文链接：『算法学习』深度可分离卷积和MobileNet_v1

一、MobileNet v1 的不足

Relu 和数据坍缩

Moblienet V2文中提出，假设在2维空间有一组由 个点组成的螺旋线 数据，经随机矩阵 映射到 维并进行ReLU运算，即：

再通过 矩阵的广义逆矩阵 将 映射回2维空间：

对比 和 发现，当映射维度 时，数据坍塌；当 时，数据基本被保存。虽然这不是严格的数学证明，但是至少说明：channel少的feature map不应后接ReLU，否则会破坏feature map。

简单说一下上图：对于一个输入图像，首先通过一个随机矩阵T将数据转换为n维，然后对这n维数据进行ReLU操作，最后再使用T的逆矩阵转换回来，实验发现当n很小的时候，后面接ReLU非线性变换的话会导致很多信息的丢失，而且维度越高还原的图片和原图越相似。

ResNet 、Relu 和神经元死亡

在神经网络训练中如果节点的值变为0就会“死掉”。因为ReLU对0值的梯度是0，后续无论怎么迭代这个节点的值都不会恢复了。而通过ResNet结构的特征复用，可以很大程度上缓解这种特征退化问题（这也从一个侧面说明ResNet为何好于VGG）。另外，一般情况训练网络使用的是float32浮点数；当使用低精度的float16时，这种特征复用可以更加有效的减缓退化。

二、Inverted residual block

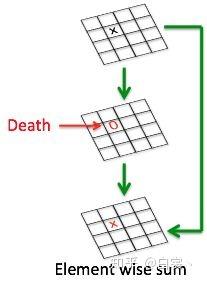
理解之前的问题后看，其实Mobilenet V2使用的基本卷积单元结构有以下特点：

• 整体上继续使用Mobilenet V1的Separable convolution降低卷积运算量
• 引入了特征复用结构，即采取了ResNet的思想
• 采用Inverted residual block结构，对Relu的缺陷进行回避

Inverted residuals 可以认为是residual block的拓展，其重点聚焦在残差网络各层的层数，进入block后会先将特征维数放大，然后再压缩回去，呈现梭子的外形，而传统残差设计是沙漏形，下面是MobileNetV1、MobileNetV2 和ResNet微结构对比：

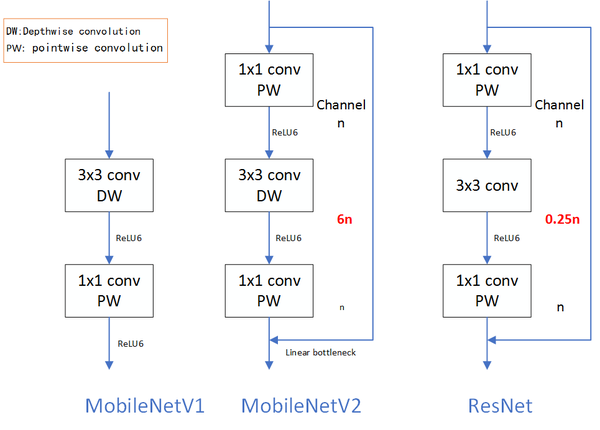可以看到MobileNetV2 和ResNet基本结构很相似。不过ResNet是先降维（0.25倍）、提特征、再升维。而MobileNetV2 则是先升维（6倍）、提特征、再降维。、

注：模型中使用 ReLU6 作为非线性层，在低精度计算时能压缩动态范围，算法更稳健。
ReLU6 定义为：f(x) = min(max(x, 0), 6)，详见 tf.nn.relu6 API

至于Linear Bottlenecks，论文中用很多公式表达这个思想，但是实现上非常简单，就是在MobileNetV2微结构中第二个PW后无ReLU6，对于低维空间而言，进行线性映射会保存特征，而非线性映射会破坏特征，实际代码如下：

def _bottleneck(inputs, nb_filters, t): 
    x = Conv2D(filters=nb_filters * t, kernel_size=(1,1), padding=‘same‘)(inputs) 
    x = Activation(relu6)(x) 
    x = DepthwiseConv2D(kernel_size=(3,3), padding=‘same‘)(x) 
    x = Activation(relu6)(x) 
    x = Conv2D(filters=nb_filters, kernel_size=(1,1), padding=‘same‘)(x) 
    # do not use activation function 
    if not K.get_variable_shape(inputs)[3] == nb_filters: 
        inputs = Conv2D(filters=nb_filters, kernel_size=(1,1), padding=‘same‘)(inputs) 
    outputs = add([x, inputs]) 
    return outputs 

相对应的，主结构堆叠上面的block 即可，下面是一个简单的版本，

def MobileNetV2_relu(input_shape, k): 
    inputs = Input(shape = input_shape) 
    x = Conv2D(filters=32, kernel_size=(3,3), padding=‘same‘)(inputs) 
    x = _bottleneck_relu(x, 8, 6) 
    x = MaxPooling2D((2,2))(x) 
    x = _bottleneck_relu(x, 16, 6)
    x = _bottleneck_relu(x, 16, 6) 
    x = MaxPooling2D((2,2))(x) 
    x = _bottleneck_relu(x, 32, 6) 
    x = GlobalAveragePooling2D()(x) 
    x = Dense(128, activation=‘relu‘)(x) 
    outputs = Dense(k, activation=‘softmax‘)(x) 
    model = Model(inputs, outputs) 
    return model

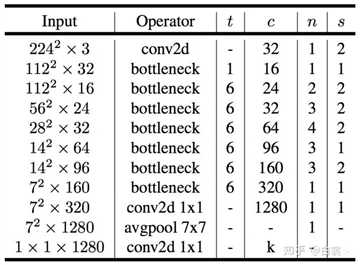
原文网络结构如下：

『算法学习』轻量级网络MobileNet_v2

标签：输入   说明   time   网络   ima   公式   实验   情况   spl   

原文地址：https://www.cnblogs.com/hellcat/p/10246646.html