标签:因此 play 算术 lock 它的 agg 采样 决策树 src
来自:https://www.cnblogs.com/pinard/p/6156009.html
集成学习有两个流派,一个是boosting,特点是各个弱学习器之间有依赖关系;一个是bagging,特点是各个弱学习器之间没依赖关系,可以并行拟合。
在集成学习原理总结中,给出bagging的原理图。
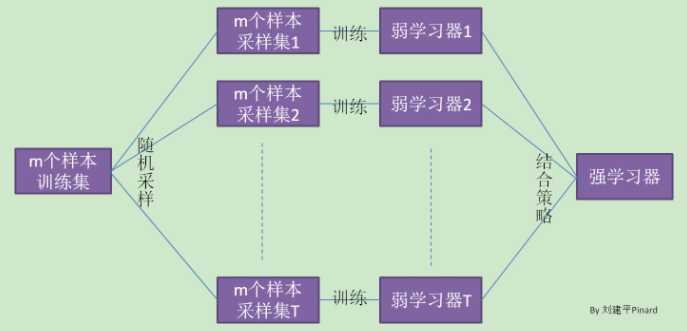
Bagging的弱学习器之间没boosting那样的联系。它的特点在“随机采样”。
随机采样常见的是自助随机采样,即有放回的随机采样。Bagging算法,一般会随机采集和训练集样本数m一样的个数的样本。这样得到的采样集和训练集样本个数相同,但样本内容不同。我们对m个样本训练集做T次的随机采样,则由于随机性,T个采样集各不相同。
注意到这和GBDT的子采样不同。GBDT的子采样是无放回采样,而Bagging的子采样是放回采样。
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是1/m。
样本在m次采样中始终不被采到的概率是:
P(一次都未被采集) = (1-1/m)m
对m取极限得到:
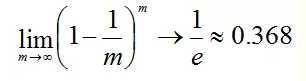
也就是说bagging的每轮随机采样中,训练集大约有36.8%的数据没被采集。
对于大约36.8%没被采样的数据,称为“袋外数据”。这些数据没参与训练集模型的拟合,但可以作为测试集用于测试模型的泛化能力,这样的测试结果称为“外包估计”。
bagging对于弱学习器没有限制,这和Adaboost一样。但是最常用的一般也是决策树和神经网络。
bagging的集合策略也比较简单,对于分类问题,通常使用简单投票法,得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题,通常使用简单平均法,对T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。
由于Bagging算法每次都进行采样来训练模型,因此泛化能力很强,对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些,也就是模型的偏倚会大一些。
标签:因此 play 算术 lock 它的 agg 采样 决策树 src
原文地址:https://www.cnblogs.com/keye/p/10252134.html