标签:循环 计算 评估 @param ++ i+1 查找算法 else lse

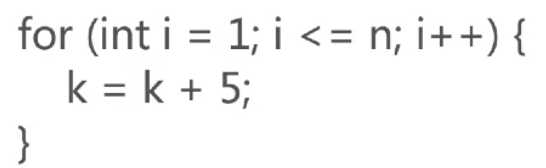
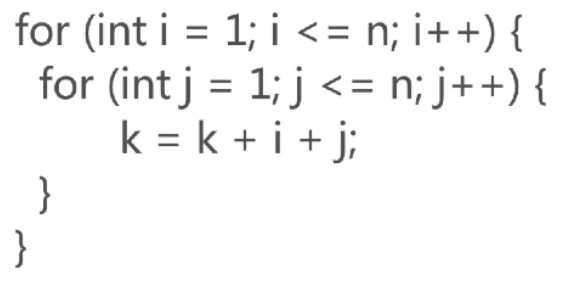
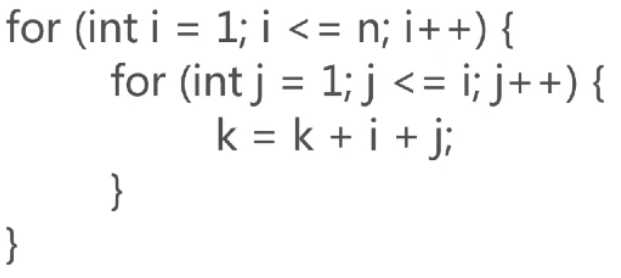

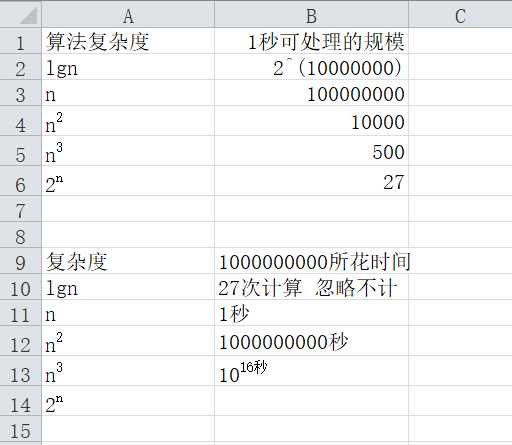
高斯解决1+2+3+....+100的办法 (1+100)*50 常数阶算法

public class Contrast { public static void main(String[] args) { int []x = new int[10000*10000]; for (int i = 0; i < x.length; i++) { x[i] = i+1; } int target = 10000*10000; long now = System.currentTimeMillis(); // 统计当前时间的方法 int index = binarySearch(x, 0, x.length-1, target); System.out.println("二分查找所需时间:"+(System.currentTimeMillis()-now)+"ms"); System.out.println(target+"所在位置为:"+index); now = System.currentTimeMillis(); index = search(x, target); System.out.println("顺序查找所需时间:"+(System.currentTimeMillis()-now)+"ms"); } /** * 二分查找 非递归 * @param arr * @param low * @param high * @param key * @return */ static int binarySearch(int arr[],int low,int high,int key){ while(low<=high){ int mid = low + ((high-low) >> 1); // (high+low) >>> 1 防止溢出,移位更加高效,同时,每次循环都需要更新 int midVal = arr[mid]; if (midVal<key) { low = mid +1; }else if (midVal>key) { high = mid - 1; }else { return mid; // key found } } return -(low + 1); // key not found } /** * 顺序查找 */ static int search(int arr[],int key){ for (int i = 0; i < arr.length; i++) { if (arr[i]==key) { return i; } } return -1; } }
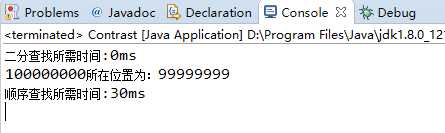
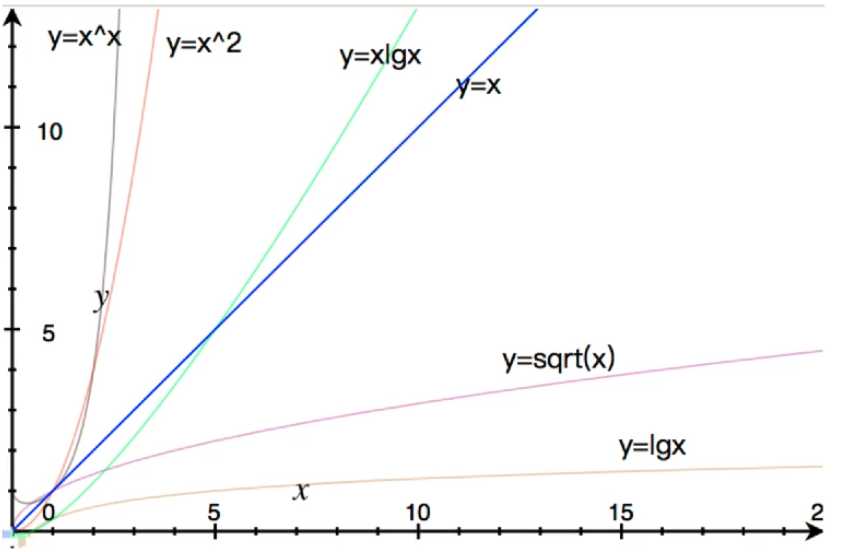
结论:二分查找时间为0ms,时间几乎可以忽略不计,可以发现这两种查找算法的时间相差很大,所以O(lgn)与O(n)的性能差别很大,
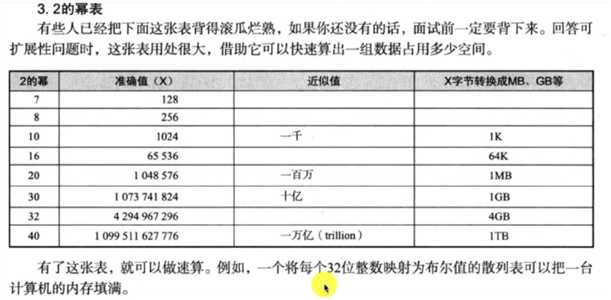
标签:循环 计算 评估 @param ++ i+1 查找算法 else lse
原文地址:https://www.cnblogs.com/xiaoyh/p/10259283.html