标签:遍历 基本 快排 次数 基于 对比 分治策略 oid master
归并排序是完全遵循分治策略的排序算法。什么是分治法?
分治法,即将原问题分解为几个规模较小的子问题,递归的求解这些子问题,之后再合并这些子问题的解,最终得到原问题的解。
归并排序遵照分治法的思想,可分为三个步骤:
同时,我们知道递归不可能无线递归下去,当分解到基本情形的时候,我们可以直接获得该问题的答案,这也是递归的出口。如果一个问题永远无法递归到基本情形,则分治法不适用。
归并排序(merge sort)的基本情形为:子数列的大小为1时,此时数列天生已排序好,开始向上回溯。
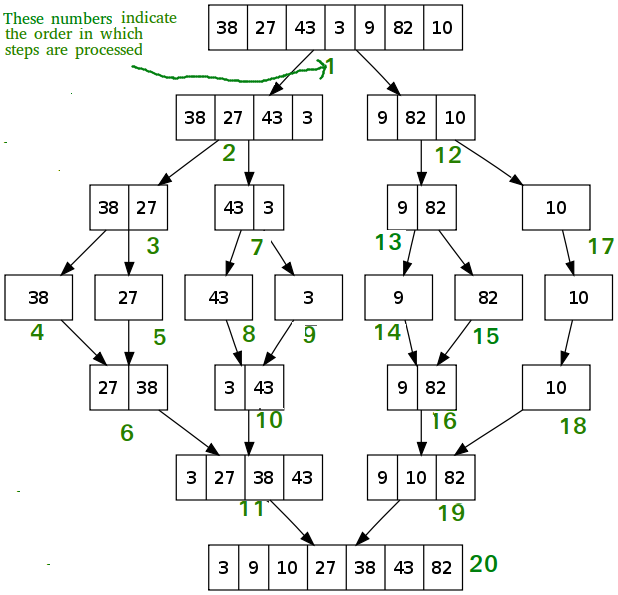
上图可见,排序数列\((38,27,43,3,9,82,10)\),我们不断的分拆数列,直至每个子数列大小为1。然后,再将子数列两两归并,逐步回溯。最终,完成排序。
以上对归并的描述可以总结以下步骤:
merge-sort(A):
if(A.length >= 1)
array A divide into array L and array R
merge-sort(L);
merge-sort(R);
merge(L,R);可以看到,核心思想就是将数组Adivide成两个子数组,在对子数组进行归并。然后merge L和R两个子数组。
merge的核心伪代码如下:
for k in (1...A.length):
if L[i] <= R[j]
A[k] = L[i];
++i;
else
L[i] >= R[j]
A[k] = R[j];
++j;merge方法也是归并排序的核心部分,但是他的思想却很简单。
由于子数组L和R都是有序的,因此只需要逐个对比两个数组的元素,其中小的元素放进数组A中,直到数组A被填满为止。
/**
* @author: luzj
* @date:
* @description: 归并排序
* 大致思想:
* 0 将数组A拆成B和C
* 1 对B和C单独排序
* 2 合并B和C成一个有序数组
* 3 B和C的排序方式同A,此为递归的基础
*/
public class MergeSort {
/**
* 排序
* @param A
* @param p
* @param r
*/
void sort(Integer[] A, int p, int r) {
if (p < r) {//开始回归的基本条件,确保最小数组大小为1结束递归
int q = Math.floorDiv(p + r, 2);
sort(A, p, q);
sort(A, q + 1, r);
merge(A, p, q, r);
}
}
/**
* 合并两个子数组
* 其实是将左右两个已经排序的子数组,进行原址排序
* @param A
* @param p 左边子数组的边界
* @param q 左右子数组的分界点
* @param r 右边子数组的边界
* 该方法的增长率为:O(n)
*/
void merge(Integer[] A, int p, int q, int r) {
int n1 = q - p + 1;//左边子数组的元素个数
int n2 = r - q; //右边子数组的元素个数
//将A数组拆成两个数组来装
Integer[] L = new Integer[n1 + 1];
Integer[] R = new Integer[n2 + 1];
for (int i = 0; i < n1; i++) {
L[i] = A[p + i];
}
for (int j = 0; j < n2; j++) {
R[j] = A[q + j + 1];
}
//哨兵,当某个子数组已经遍历完后还接着遍历时,哨兵将很好的阻止越界并且将遍历转向另一个子数组
L[n1] = Integer.MAX_VALUE;
R[n2] = Integer.MAX_VALUE;
int i = 0, j = 0;
//重排,每次都进行比较,将较小的装进A数组(如果是降序排列,则塞较大的)
for (int k = p; k <= r; k++) {
if (L[i] <= R[j]) {
A[k] = L[i];
i++;
} else {
A[k] = R[j];
j++;
}
}
}
public static void main(String[] args) {
Integer[] A = {5,2,4,7,1,3,2,6};
new MergeSort().sort(A,0,A.length-1);
for (int i = 0; i < A.length; i++) {
System.out.print(A[i]+" ");
}
}
}归并排序的时间复杂度为:\(nlg(n)\)。
我们可以大致算一笔账:
每一次数组将会分裂成两份,即从中间一分为二,最终形成一个二叉树。那么这个二叉树多少层呢,答案是\(log_2{n}+1\)。
同时注意到,每一次递归的时间复杂度都来自merge(A) 方法,而merge方法复杂度为\(c*{n_i}\).每一层都有\(c({n_1+n_2+...+n_i})\),即\(c*(n)\)的复杂度。因此,可以看到每一层不管有多少个节点,他的复杂度都是\(c*{n}\).
最终可得,merger-sort的复杂度为:\(O(nlg({n}))\)。
这里还有一个结论,就是所有基于比较的排序方法,他的性能上限都是\(O(n*lg{(n)})\),因此快排的平均时间复杂度也不超过这个数。在《算法导论》中,有一个基于决策树的精彩论述,有兴趣的同学可以研读一下。
归并排序使用分治法,时间复杂度为\(nlg(n)\)。
标签:遍历 基本 快排 次数 基于 对比 分治策略 oid master
原文地址:https://www.cnblogs.com/Franken-Fran/p/merger-sort.html