快速排序

标签：des   均衡   算法   sort   性能   script   插入排序   不同的   最好   

快速排序

同归并排序一样，快排也使用了分治法的思想。不同的是，归并的思路是将两个有序数列合并成一个有序数列，并将该步骤不断的递归下去。而快排的思路是如果数列中的每一个数都比他的左边的所有数都大，比他右边的所有数都小，那么该数列就一定是升序排列的。

步骤描述

分解，将数组\(A[p...r]\)分成两个子数组\(A[p...q-1]\)和\(A[q+1...r]\)。使得\(A[q]\)大于等于\(A[p...q-1]\)的每一个数，同时大于等于\(A[q+1...r]\)的每一个数

递归,对子数组\(A[p...q-1]\)和\(A[p+1...r]\)分别执行快排

出口,当子数组大小为1的时候,数组天然有序,此时停止递归,开始回溯

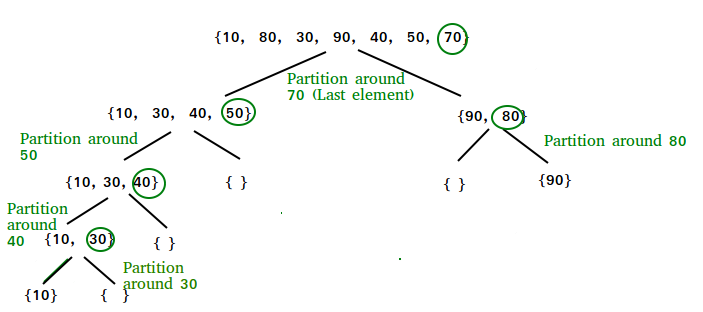
上图可见,对数列\((10,80,30,90,40,50,70)\)排序.第一次选取70作为中间值,将数列分为\(L = (10,30,40,50)\) 和 \(R = (90,80)\).后面的以此类推,知道子数组大小为1或者0为止

伪代码

quickSort(A,p,r):
    if(p < r)
        q = partition(A,p,r);
        quicksort(A,p,q-1)
        quicksort(A,q+1,r)

以上是快排的伪代码,当\(A.length > 1\)的时候,即对该数组进行 partition 操作,然后对子数组递归

其中 partition 就是二分数组的方法,返回值为中间值的索引,一下为 partition 的操作描述

partition(A,p,r)
    x = A[r] //选取最后一个值为中间值,以他为标的分割数组
    i= p-1
    for j in (p...r-1)
        if A[j] <= x
            ++i
            交换 A[i] 和 A[j]
    //经过一系列交换后,导致A[i+1]左边的都小于A[r],右边的都大于A[r]
    交换 A[i+1] 和 A[r] 
    // (i+1) 就是A[r]的索引,作为返回值
    return i+1

以上是 partition 操作的伪代码,大致思路就是选取最后一个值为中间值,然后使用两个游标\(i,j\)开始遍历数组.\(i+1\)左边的都小于\(A[r]\),i到j的都是大于A[r]的.最终,\(j == r-1\)

代码实现(Java)

/**
 * @author: luzj
 * @date: 
 * @description: 快排,已测试
 */
public class QuickSort {

    void quickSort(Integer[] A, int p, int r) {
        if (p < r) {
            int q = partition(A, p, r);
            quickSort(A, p, q - 1);
            quickSort(A, q + 1, r);
        }
    }

    private int partition(Integer[] A, int p, int r) {
        Integer x = A[r];
        int i = p - 1;
        for (int j = p; j < r; j++) {
            if (A[j] <= x) {
                i++;
                Integer tmp0 = A[i];
                A[i] = A[j];
                A[j] = tmp0;
            }
        }
        Integer tmp1 = A[i + 1];
        A[i + 1] = A[r];
        A[r] = tmp1;
        return i + 1;
    }

    public static void main(String[] args) {
        Integer[] A = {13,19,9,5,12,8,7,4,21,2,6,11};
        new QuickSort().quickSort(A,0,A.length-1);
        for (int i = 0; i < A.length; i++) {
            System.out.print(A[i]+" ");
        }
    }
}

时间复杂度

快排的时间复杂度依赖于输入的分布,平均情况下快排的时间复杂度为\(O(nlog(n))\).在均衡分割的时候(即\(A[r]\)的索引落在数组中间),性能最好.

其实,即使每次数组分割都很不均匀的情况下,比如99:1的比例分割,快排的期望运行时间仍未\(O(nlog(n))\).算法导论的７.4.2部分给出期望运行时间分析。

最坏的情况下,快排的运行时间为\(O(n^2)\).当输入为一个有序数列的时候,快排坍缩为插入排序.每一次分叉只能分出一个数组出来,因此无法保证二叉树为对数高度.

小结

快排同归并排序一样，使用的是分治法．时间复杂度依赖于输入分布，平均期望运行时间为\(O(nlog(n))\)

参考

• 《算法导论》
• 维基百科－快速排序

快速排序

标签：des   均衡   算法   sort   性能   script   插入排序   不同的   最好   

原文地址：https://www.cnblogs.com/Franken-Fran/p/quickSort.html