标签:划算 结构 切割 算法实现 for == 自己 -- pen
从斐波那契数列看动态规划
斐波那契数列:

def fibnacci(n): if n == 1 or n==2: return 1 else: return fibnacci(n-1)+fibnacci(n-2) # print(fibnacci(100)) #--------------------------------------------------------- # 递归会出现子问题的重复计算 # f(6) = f(5)+f(4) # f(5) = f(4)+f(3) # f(4) = f(3)+f(2) # f(3) = f(2)+f(1) # 动态规划(DP)的思想=最优子结构==>递推式子(需要自己总结) + 重复子问题 def fibnacci_no_recurision(n): f = [0,1,1] if n>2: for i in range(n-2): num = f[-1]+f[-2] f.append(num) print(f) return f[n] # n==3 i==0 num=2 f=[0,1,1,2] # 子问题重复 # n==4 i==0 num=2 f=[0,1,1,2];i==1 num=3 f=[0,1,1,2,3] print(fibnacci_no_recurision(4))

-----------------------------------------------------------------------------------------------------------------------------------------------------
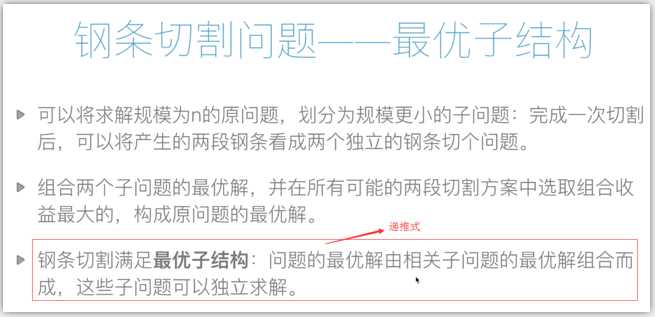

钢条切割问题:自顶向下实现
时间复杂度O(2^n)---不采取
递归算法由于重复求解相同子问题,效率低
动态规划的思想:
每一次子问题只求解一次,保存求解结果
之后需要此问题时,只需要查找保存的结果
钢条切割问题:自底向上实现


标签:划算 结构 切割 算法实现 for == 自己 -- pen
原文地址:https://www.cnblogs.com/foremostxl/p/10263423.html