标签:因此 攻击 多项式 十六进制 subbyte tostring 产生 decrypt 最大
高级数据加密标准(Advanced Encryption Standard),简称AES,由美国政府于1997年开始公开征集的新的数据加密标准算法。经过三轮筛选,美国政府最终于2000年10月2日正式宣布选中密码学家Joan Daemen和Vincent Rijmen提出的RINJDAEL算法作为AES。
RINJDAEL算法之所以能够最终被选为AES的原因是其安全、性能好、效率高、实用、灵活。
RINJDAEL算法是一个数据块长度和密钥长度都可变的分组加密算法,其数据块长度和密钥长度都可独立地选定为大于等于128位且小于等于256位的32位的任意倍数。而美国颁布AES时却规定数据块的长度为128位,密钥的长度可分别选择为128位、192位或256位。
RINJDAEL算法仍然采用分组密码的一种通用结构:对轮函数实施迭代的结构。只是轮函数结构采用的是代替/置换的网络结构(SP结构)。
AES算法中的许多运算是按字节和4字节的字来定义的。把一个字节看成是在有限域GF(28)上的一个元素,把一个4字节的字看成是系数取自GF(28),并且次数小于4次的多项式。
一个由比特位b7b6b5b4b3b2b1b0组成的字节B可表示成系数为0或1的二进制多项式:b7x7+b6x6+b5x5+b4x4+b3x3+b2x2+b1x+b0。例如,字节B=10011011与二进制多项式b(x)=x7+x4+x3+x+1相对应。
在GF(28)上的加法定义为二进制多项式的加法,其系数模2相加。
e.m.
(x7+x4+x3+x+1)+(x6+x5+x3+x2+x+1)=x7+x6+x5+x4+x2
在GF(28)上的乘法定义为二进制多项式的乘积,如果乘积次数大于7次则模一个次数为8的不可约二进制多项式。
e.m.对于不可约多项式m(x)=x8+x4+x3+x+1,
(x6+x4+x2+x+1)(x7+x+1)
=(x13+x11+x9+x8+x6+x5+x4+x3+1)(mod x8+x4+x3+x+1)
=x7+x6+1
在GF(28)中,二进制多项式b(x)的乘法逆为满足a(x)b(x)=1的二进制多项式a(x),并记为
a(x)=b-1(x)。其中,‘00‘的乘法逆为其本身。
可以使用扩展欧几里得算法求得乘法逆,也可以直接将‘00‘~‘FF‘这128中情况全部试代求得乘法逆。
e.m.对于不可约多项式m(x)=x8+x4+x3+x+1,因为
x6+x2+x+1=(x8+x4+x3+x+1)+(x6+x4+x2+x+1)
x4=(x6+x4+x2+x+1)+(x6+x2+x+1)=(x8+x4+x3+x+1)+(x2+1)(x6+x4+x2+x+1)
x2+x+1=(x6+x2+x+1)+x2·x4=(x2+1)(x8+x4+x3+x+1)+x4(x6+x4+x2+x+1)
x=x4+(x2+x)(x2+x+1)=x6+x2+x+1=(x4+x+1)(x8+x4+x3+x+1)+(x6+x5+x2+1)(x6+x4+x2+x+1)
1=(x2+x+1)+(x+1)x=(x5+x4)(x8+x4+x3+x+1)+(x7+x5+x4+x3+x2+x+1)(x6+x4+x2+x+1)
所以
(x6+x4+x2+x+1)(x7+x5+x4+x3+x2+x+1)=1
即
(x6+x4+x2+x+1)-1=x7+x5+x4+x3+x2+x+1
在GF(28)中,倍乘函数 xtime(b(x))定义为x·b(x) (mod m(x))。即把字节B左移一位,若结果次数大于7次,则加上不可约多项式m(x)。
e.m.对于不可约多项式m(x)=x8+x4+x3+x+1,
x(x6+x4+x2+x+1)=x7+x5+x3+x2+x
x(x7+x5+x3+x2+x)=(x8+x6+x4+x3+x2)+(x8+x4+x3+x+1)=x6+x2+x+1
有限域GF(28)上的多项式是系数取自GF(28)域元素的多项式。这样,一个4字节的字与一个次数小于4次的GF(28)上的多项式相对应。例如,字c=‘03010102‘与多项式c(x)=‘03‘x3+‘01‘x2+‘01‘x+‘02‘相对应。
GF(28)上的多项式的加法定义为相应项系数相加。所以,在域GF(28)上的两个4字节的字相加也就是按位异或。
e.m.
(‘03‘x3+‘01‘x2+‘01‘x+‘02‘)+(‘0B‘x3+‘0D‘x2+‘09‘x+‘0E‘)=‘08‘x3+‘0C‘x2+‘08‘x+‘0C‘
GF(28)上的多项式a(x)=a3x3+a2x2+a1x+a0和b(x)=b3x3+b2x2+b1x+b0相乘,如果乘积次数超过4次,则模x4+1。即对于c(x)=a(x)b(x)=c3x3+c2x2+c1x+c0,
c0=a0b0⊕a3b1⊕a2b2⊕a1b3
c1=a1b0⊕a0b1⊕a3b2⊕a2b3
c2=a2b0⊕a1b1⊕a0b2⊕a3b3
c3=a3b0⊕a2b1⊕a1b2⊕a0b3
GF(28)上的多项式b(x)=b3x3+b2x2+b1x+b0的倍乘x·b(x)=b2x3+b1x2+b0x+b3。即多项式的系数循环左移一位。
在AES算法中,加解密要经过多次数据变换操作,每一次变换操作都会产生一个中间结果,这个结果称为状态。把状态表示为一个4行Nb列的二维字节数组,其中Nb为数据块长度除以32。因为状态数组有4行,所以状态数组的每一列便为一个4字节的字。
例如,对于长度为128的数据块B15B14...B1B0,Nb=128÷32=4,即该数据块可以表示为状态数组
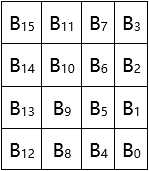
AES算法中规定数据块长度为128位,即Nb=128÷32=4。
类似地,密钥也可以表示为4行Nk列的二维字节数组,其中Nk为密钥长度除以32。同样地,密钥数组的每一列为一个4字节的字。
例如,对于长度为128的密钥K15K14...K1K0,Nk=128÷32=4,即该密钥可以表示为密钥数组
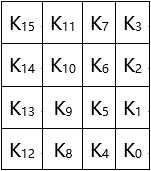
AES算法中规定密钥长度为128位、192位或256位,即Nk取值为4、6或8。
AES算法的迭代轮数Nr由Nb和Nk共同决定:
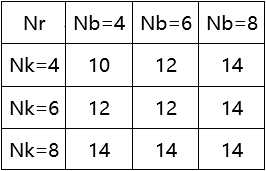
AES规定Nb=4,所以对应Nk取值4、6、8,Nr取值分别为10、12、14,即在Nb=4的情况下,Nr=Nk+6。
在AES算法中,不可约多项式建议为:m(x)=x8+x4+x3+x+1,其系数的十六进制表示为m=‘11B‘。
AES的轮函数由以下3层组成:
1.非线性层:进行非线性S盒变换,由16个S盒并置而成,起混淆的作用;
2.线性混合层:进行行移位变换和列混合变换以确保多轮之上的高度扩散;
3.密钥加层:进行轮密钥加变换,将轮密钥简单地异或到中间状态上。
S盒变换是按字节进行的代替变换,是作用在状态中每个字节上的一种非线性字节变换。
加密过程中的S盒变换按以下2步进行:
(1)把字节的值用它的乘法逆来代替;
(2)进行如下的仿射变换:
xi‘=xi⊕xi+4⊕xi+5⊕xi+6⊕xi+7
y7y6y5y4y3y2y1y0=(x7‘x6‘x5‘x4‘x3‘x2‘x1‘x0‘)⊕(01100011)

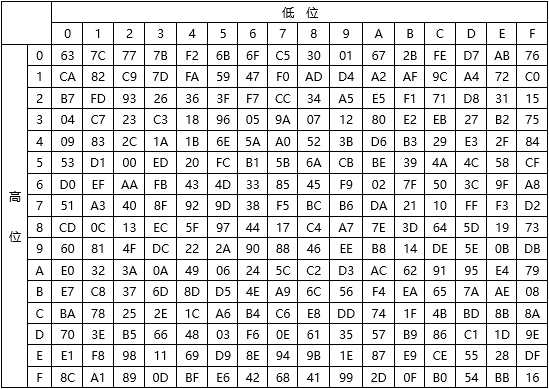
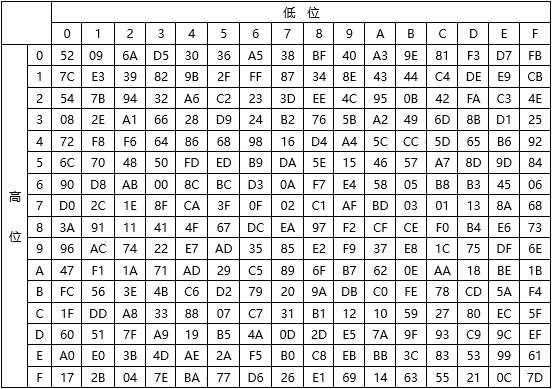
加密过程的S盒表如下:
解密过程中的S盒变换按以下2步进行:
(1)进行如下的仿射变换:
xi‘=xi+2⊕xi+5⊕xi+7
y7y6y5y4y3y2y1y0=(x7‘x6‘x5‘x4‘x3‘x2‘x1‘x0‘)⊕(00000101)

(2)把字节的值用它的乘法逆来代替。
解密过程的S盒表如下:
行移位变换是对状态的行进行循环移位变换。移位值C1、C2、C3与Nb有关:
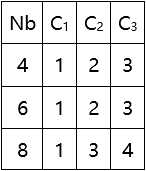
AES规定Nb=4,所以C1=1,C2=2,C3=3。
加密过程中的行移位变换,状态的第0行不移位,第1行循环左移C1字节,第2行循环左移C2字节,第3行循环左移C3字节。
解密过程中的行移位变换,状态的第0行不移位,第1行循环左移Nb-C1字节,第2行循环左移Nb-C2字节,第3行循环左移Nb-C3字节。
列混合变换是对状态的列进行混合变换。
加密过程中的列混合变换,把状态中的每一列看作GF(28)上的多项式,并与固定多项式c(x)=‘03‘x3+‘01‘x2+‘01‘x+‘02‘相乘。
解密过程中的列混合变换,把状态中的每一列看作GF(28)上的多项式,并与固定多项式c(x)=‘0B‘x3+‘0D‘x2+‘09‘x+‘0E‘相乘。
轮密钥加变换是利用轮密钥对状态进行模2相加的变换。轮密钥长度等于数据块长度。在这个操作中,轮密钥被简单地异或到状态中去。
轮密钥根据轮密钥产生算法由主密钥产生得到。轮密钥产生分2步进行:密钥扩展和轮密钥选择,且遵循以下原则:
1.轮密钥的比特总数为数据块长度与轮数加1的,即Nb(Nr+1)。
2.首先将用户密钥扩展为一个扩展密钥。
3.再从扩展密钥中选出轮密钥:第1个轮密钥由扩展密钥中的前Nb个字组成,第2个轮密钥由接下来的Nb个字组成,以此类推。
加密过程的轮密钥产生分以下2步进行:
1.密钥扩展:用1个字元素的一维数组W[Nb(Nr+1)]存储扩展密钥。把主密钥放在数组W最开始的Nk个字中,其他的字由它前面的字经过处理(处理过程参照代码部分)后得到。分Nk≤6和Nk>6两种情况进行密钥扩展,两种情况的密钥扩展策略稍有不同。
2.轮密钥选择:轮密钥i由轮密钥缓冲区W[Nb*i]到W[Nb*(i+1)-1]的字组成。
解密过程的轮密钥产生分以下2步进行:
1.加密过程的轮密钥产生。
2.把解密过程的列混合变换应用到除第一个和最后一个轮密钥之外的所有轮密钥上。
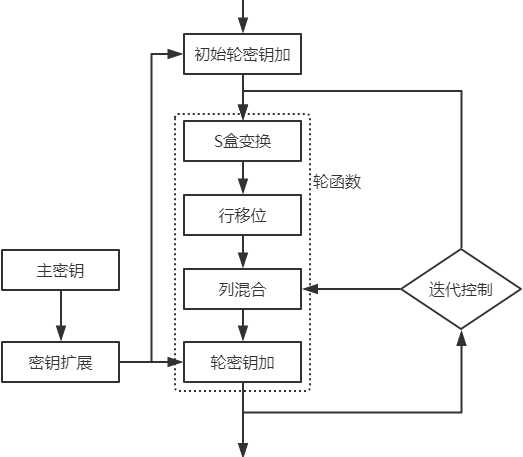
无论是加密过程还是解密过程,都由以下部分组成:
1.一个初始轮密钥加。
2.Nr-1轮的标准轮函数(包括S盒变换、行移位、列混合、轮密钥加)。
3.最后一轮的非标准轮函数(只包括S盒变换、行移位、轮密钥加,不需要列混合)。
AES的安全涉及策略是宽轨迹策略。宽轨迹策略是针对差分攻击和先行攻击提出来的。它的最大优点是可以给出算法的最佳差分特征的概率以及最佳线性逼近的偏差界,由此可以分析算法的抵抗差分攻击和线性攻击的能力。从而确保密码算法具有所需要的抵抗差分攻击和线性攻击的能力,确保密码算法的安全。
AES的主要密码部件S盒和列混合都设计得相当好。其列混合的一个重要密码学指标分支数达到了最佳值,其S盒在非线性度、自相关性、差分均匀性、代数免疫性等主要密码学指标方面都达到相当好的水平。
然而,AES中的列混合的扩散度不够,密钥扩展的非线性不够,而且缺少抵抗侧信道分析的设计。这些不足之处给密码分析提供了可乘之机。
AES的加解密算法采用不同的密钥扩展算法,而且都使用了非线性的S盒变换,并且在扩展产生每一轮密钥中使用不同的轮函数。这些措施使得AES不存在弱密钥和半弱密钥,也就是说,在AES加解密算法中,对密钥的选择没有除长度外的任何限制。
AES的密钥长度可变,因此能够适应不同的安全应用环境。即使今后计算能力和攻击能力提高了,只要及时提高密钥的长度,便可获得满意的安全,因此密码的安全使用寿命长。
1 public class word { 2 byte[] word; 3 4 public word(byte[] b) { 5 word = new byte[4]; 6 for (int i = 0; i < 4; i++) 7 word[i] = b[i]; 8 } 9 10 public word(word w) { 11 word = new byte[4]; 12 for (int i = 0; i < 4; i++) 13 word[i] = w.word[i]; 14 } 15 16 @Override 17 public String toString() { 18 String str = ""; 19 for (byte b : word) 20 str += Integer.toHexString((b & 0xff) + 0x100).substring(1); 21 return str; 22 } 23 24 /** 25 * 在GF(2^8)上的多项式加法 26 * @param a 27 * @param b 28 * @return 29 */ 30 static word add(word a, word b) { 31 word c = new word(new byte[4]); 32 for (int i = 0; i < 4; i++) 33 c.word[i] = add(a.word[i], b.word[i]); 34 return c; 35 } 36 37 /** 38 * 在GF(2^8)上的多项式乘法 39 * @param a 40 * @param b 41 * @return 42 */ 43 static word multiply(word a, word b) { 44 word c = new word(new byte[4]); 45 c.word[0] = add( 46 add( 47 add( 48 multiply(a.word[0], b.word[0]), multiply(a.word[3], b.word[1])), 49 multiply(a.word[2], b.word[2])), 50 multiply(a.word[1], b.word[3])); 51 c.word[1] = add( 52 add( 53 add( 54 multiply(a.word[1], b.word[0]), multiply(a.word[0], b.word[1])), 55 multiply(a.word[3], b.word[2])), 56 multiply(a.word[2], b.word[3])); 57 c.word[2] = add( 58 add( 59 add( 60 multiply(a.word[2], b.word[0]), multiply(a.word[1], b.word[1])), 61 multiply(a.word[0], b.word[2])), 62 multiply(a.word[3], b.word[3])); 63 c.word[3] = add( 64 add( 65 add( 66 multiply(a.word[3], b.word[0]), multiply(a.word[2], b.word[1])), 67 multiply(a.word[1], b.word[2])), 68 multiply(a.word[0], b.word[3])); 69 return c; 70 } 71 72 /** 73 * 在GF(2^8)上的多项式倍乘 74 * @param a 75 * @return 76 */ 77 static word xtime(word a) { 78 word b = new word(new byte[4]); 79 for (int i = 0; i < 4; i++) 80 b.word[i] = a.word[(i + 1) % 4]; 81 return b; 82 } 83 /**********************************************************************************/ 84 static int m = 0x11b; //m=100011011 85 86 /** 87 * 在GF(2^8)上的加法 88 * @param a 89 * @param b 90 * @return 91 */ 92 static byte add(byte a, byte b) { 93 return (byte) (a ^ b); 94 } 95 96 /** 97 * 在GF(2^8)上的求模 98 * @param a 99 * @param b 100 * @return 101 */ 102 static byte mod(int a, int b) { 103 String str_a = Integer.toBinaryString(a); 104 String str_b = Integer.toBinaryString(b); 105 if (str_a.length() < str_b.length()) 106 return (byte) a; 107 return mod(a ^ (b << (str_a.length() - str_b.length())), b); 108 } 109 110 /** 111 * 在GF(2^8)上的乘法 112 * @param a 113 * @param b 114 * @return 115 */ 116 static byte multiply(byte a, byte b) { 117 int op = a & 0xff; 118 char[] c = Integer.toBinaryString((b & 0xff) + 0x100).substring(1).toCharArray(); 119 int r = 0; 120 for (int i = 0; i < c.length; i++) 121 if (c[i] == ‘1‘) 122 r ^= op << (7 - i); 123 return mod(r, m); 124 } 125 126 /** 127 * 在GF(2^8)上的乘法逆 128 * @param a 129 * @return 130 */ 131 static byte inverse(byte a) { 132 if (a == 0) return 0; 133 byte b = -128; 134 while (mod(multiply(a, b), m) != 1) 135 b++; 136 return b; 137 } 138 139 /** 140 * 在GF(2^8)上的倍乘 141 * @param a 142 * @return 143 */ 144 static byte xtime(byte a) { 145 int r = (a & 0xff) << 1; 146 if (r > 127) 147 return mod(r, m); 148 return (byte) r; 149 } 150 }
1 /** 2 * 仿射变换 3 * @param b 4 * @param sign C:加密 D:解密 5 * @return 6 */ 7 static byte AffineTransformation(byte b, char sign) { 8 byte[] x = Integer.toBinaryString((b & 0xff) + 0x100).substring(1).getBytes(); 9 for (int i = 0; i < x.length; i++) x[i] -= ‘0‘; 10 if (sign == ‘C‘) { 11 byte[] x_ = new byte[8]; 12 byte b_ = 0; 13 for (int i = 0; i < 8; i++) { 14 x_[i] = (byte) (x[i] ^ x[(i + 1) % 8] ^ x[(i + 2) % 8] ^ x[(i + 3) % 8] ^ x[(i + 4) % 8]); 15 b_ += x_[i] * Math.pow(2, 7 - i); 16 } 17 return (byte) (b_ ^ 0x63); 18 } else { 19 byte[] x_ = new byte[8]; 20 byte b_ = 0; 21 for (int i = 0; i < 8; i++) { 22 x_[i] = (byte) (x[(i + 1) % 8] ^ x[(i + 3) % 8] ^ x[(i + 6) % 8]); 23 b_ += x_[i] * Math.pow(2, 7 - i); 24 } 25 return (byte) (b_ ^ 0x05); 26 } 27 }
1 /** 2 * 加密密钥扩展 3 * @param CipherKey 4 * @return 5 */ 6 static word[][] KeyExpansion(word[] CipherKey) { 7 word[] W = new word[Nb * (Nr + 1)]; 8 //密钥扩展 9 word Temp; 10 if (Nk <= 6) { 11 for (int i = 0; i < Nk; i++) 12 W[i] = CipherKey[i]; 13 for (int i = Nk; i < W.length; i++) { 14 Temp = new word(W[i - 1]); 15 if (i % Nk ==0) 16 Temp = word.add(SubByte(Rotl(Temp)), Rcon(i / Nk)); 17 W[i] = word.add(W[i - Nk], Temp); 18 } 19 } else { 20 for (int i = 0; i < Nk; i++) 21 W[i] = CipherKey[i]; 22 for (int i = Nk; i < W.length; i++) { 23 Temp = new word(W[i - 1]); 24 if (i % Nk ==0) 25 Temp = word.add(SubByte(Rotl(Temp)), Rcon(i / Nk)); 26 else if (i % Nk == 4) 27 Temp = SubByte(Temp); 28 W[i] = word.add(W[i - Nk], Temp); 29 } 30 } 31 //轮密钥选择 32 word[][] RoundKey = new word[Nr + 1][Nb]; 33 for (int i = 0; i < Nr + 1; i++) 34 for (int j = 0; j < Nb; j++) 35 RoundKey[i][j] = W[Nb * i + j]; 36 return RoundKey; 37 }
1 static word SubByte(word a) { 2 word w = new word(a); 3 for (int i = 0; i < 4; i++) { 4 //乘法逆代替 5 w.word[i] = word.inverse(w.word[i]); 6 //仿射变换 7 w.word[i] = AffineTransformation(w.word[i], ‘C‘); 8 } 9 return w; 10 } 11 12 static word Rotl(word a) { 13 word w = new word(a); 14 byte b = w.word[0]; 15 for (int i = 0; i < 3; i++) 16 w.word[i] = w.word[i + 1]; 17 w.word[3] = b; 18 return w; 19 } 20 21 static word Rcon(int n) { 22 word Rcon = new word(new byte[4]); 23 byte RC = 1; 24 for (int i = 1; i < n; i++) 25 RC = word.xtime(RC); 26 Rcon.word[0] = RC; 27 return Rcon; 28 }
1 /** 2 * 解密密钥扩展 3 * @param CipherKey 4 * @return 5 */ 6 static word[][] InvKeyExpansion(word[] CipherKey) { 7 word[][] InvRoundKey = KeyExpansion(CipherKey); 8 for (int i = 1; i < Nr; i++) 9 InvRoundKey[i] = InvMixColumn(InvRoundKey[i]); 10 return InvRoundKey; 11 }
1 /** 2 * S盒变换 3 * @param state 4 * @return 5 */ 6 static word[] ByteSub(word[] state) { 7 for (int i = 0; i < Nb; i++) 8 for (int j = 0; j < 4; j++) { 9 //乘法逆代替 10 state[i].word[j] = word.inverse(state[i].word[j]); 11 //仿射变换 12 state[i].word[j] = AffineTransformation(state[i].word[j], ‘C‘); 13 } 14 return state; 15 }
1 /** 2 * S盒逆变换 3 * @param state 4 * @return 5 */ 6 static word[] InvByteSub(word[] state) { 7 for (int i = 0; i < Nb; i++) 8 for (int j = 0; j < 4; j++) { 9 //仿射变换 10 state[i].word[j] = AffineTransformation(state[i].word[j], ‘D‘); 11 //乘法逆代替 12 state[i].word[j] = word.inverse(state[i].word[j]); 13 } 14 return state; 15 }
1 /** 2 * 行移位变换 3 * @param state 4 * @return 5 */ 6 static word[] ShiftRow(word[] state) { 7 byte[][] b = new byte[4][Nb]; 8 for (int j = 0; j < Nb; j++) 9 for (int i = 0; i < 4; i++) 10 b[i][j] = state[j].word[i]; 11 for (int i = 1; i < 4; i++) 12 for (int k = 0; k < i; k++) { 13 byte t = b[i][0]; 14 for (int j = 0; j < Nb - 1; j++) 15 b[i][j] = b[i][j + 1]; 16 b[i][Nb - 1] = t; 17 } 18 for (int j = 0; j < Nb; j++) 19 for (int i = 0; i < 4; i++) 20 state[j].word[i] = b[i][j]; 21 return state; 22 }
1 /** 2 * 行移位逆变换 3 * @param state 4 * @return 5 */ 6 static word[] InvShiftRow(word[] state) { 7 byte[][] b = new byte[4][Nb]; 8 for (int j = 0; j < Nb; j++) 9 for (int i = 0; i < 4; i++) 10 b[i][j] = state[j].word[i]; 11 for (int i = 1; i < 4; i++) 12 for (int k = 0; k < Nb - i; k++) { 13 byte t = b[i][0]; 14 for (int j = 0; j < Nb - 1; j++) 15 b[i][j] = b[i][j + 1]; 16 b[i][Nb - 1] = t; 17 } 18 for (int j = 0; j < Nb; j++) 19 for (int i = 0; i < 4; i++) 20 state[j].word[i] = b[i][j]; 21 return state; 22 }
1 /** 2 * 列混合变换 3 * @param state 4 * @return 5 */ 6 static word[] MixColumn(word[] state) { 7 byte[] b = {(byte) 0x02, (byte) 0x01, (byte) 0x01, (byte) 0x03}; 8 word a = new word(b); 9 for (int i = 0; i < Nb; i++) 10 state[i] = word.multiply(a, state[i]); 11 return state; 12 }
1 /** 2 * 列混合逆变换 3 * @param state 4 * @return 5 */ 6 static word[] InvMixColumn(word[] state) { 7 byte[] b = {(byte) 0x0E, (byte) 0x09, (byte) 0x0D, (byte) 0x0B}; 8 word a = new word(b); 9 for (int i = 0; i < Nb; i++) 10 state[i] = word.multiply(a, state[i]); 11 return state; 12 }
1 /** 2 * 轮密钥加变换 3 * @param state 4 * @param key 5 * @return 6 */ 7 static word[] AddRoundKey(word[] state, word[] key) { 8 for (int i = 0; i < Nb; i++) 9 state[i] = word.add(state[i], key[i]); 10 return state; 11 }
1 /** 2 * 加密 3 * @param plaintext 4个字长度的明文 4 * @param CipherKey 4、6或8个字长度的密钥 5 * @return 6 */ 7 public static word[] encrypt(word[] plaintext, word[] CipherKey) { 8 Nb = 4; 9 Nk = CipherKey.length; 10 Nr = Nk + 6; 11 //加密密钥扩展 12 RoundKey = KeyExpansion(CipherKey); 13 word[] ciphertext = new word[plaintext.length]; 14 for (int i = 0; i < plaintext.length; i++) 15 ciphertext[i] = new word(plaintext[i]); 16 //初始轮密钥加 17 ciphertext = AddRoundKey(ciphertext, RoundKey[0]); 18 //轮函数 19 for (int i = 1; i < Nr + 1; i++) { 20 //S盒变换 21 ciphertext = ByteSub(ciphertext); 22 //行移位 23 ciphertext = ShiftRow(ciphertext); 24 //列混合 25 if (i != Nr) ciphertext = MixColumn(ciphertext); 26 //轮密钥加 27 ciphertext = AddRoundKey(ciphertext, RoundKey[i]); 28 } 29 return ciphertext; 30 }
1 /** 2 * 解密 3 * @param ciphertext 4个字长度的密文 4 * @param CipherKey 4、6或8个字长度的密钥 5 * @return 6 */ 7 public static word[] decrypt(word[] ciphertext, word[] CipherKey) { 8 Nb = 4; 9 Nk = CipherKey.length; 10 Nr = Nk + 6; 11 //解密密钥扩展 12 InvRoundKey = InvKeyExpansion(CipherKey); 13 word[] plaintext = new word[ciphertext.length]; 14 for (int i = 0; i < ciphertext.length; i++) 15 plaintext[i] = new word(ciphertext[i]); 16 //初始轮密钥加 17 plaintext = AddRoundKey(plaintext, InvRoundKey[Nr]); 18 //轮函数 19 for (int i = Nr - 1; i >= 0; i--) { 20 //S盒变换 21 plaintext = InvByteSub(plaintext); 22 //行移位 23 plaintext = InvShiftRow(plaintext); 24 //列混合 25 if (i != 0) plaintext = InvMixColumn(plaintext); 26 //轮密钥加 27 plaintext = AddRoundKey(plaintext, InvRoundKey[i]); 28 } 29 return plaintext; 30 }
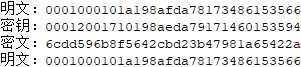
明文:0001000101a198afda78173486153566
密钥:00012001710198aeda79171460153594
张焕国,唐明.密码学引论(第三版).武汉大学出版社,2015年
标签:因此 攻击 多项式 十六进制 subbyte tostring 产生 decrypt 最大
原文地址:https://www.cnblogs.com/mx-lqk/p/10285379.html