标签:image 后缀 can include 枚举 稳定性 print std 难点
最好会基数排序,实在不行可以快速排序 (倍增算法的时间复杂度会从\(\Theta (n\log n)~\to~\Theta (n\log^2 n)\))
这个大家应该都知道,比方说有一个字符串\(a~b~c~d~e~f\),那么它的后缀就是:
后缀1: \(a~b~c~d~e~f\)
? 2: \(~~~b~c~d~e~f\)
? 3: \(~~~~~c~d~e~f\)
? 4: \(~~~~~~~~d~e~f\)
? 5: \(~~~~~~~~~~e~f\)
? 6: \(~~~~~~~~~~~~~~f\)
为了行文方便,以下简称 以第 \(i\) 位字符为开头的后缀 为 后缀 \(i\)
所谓后缀数组,其实就是将字符串 \(S\) 的后缀按从小到大的顺序(字典序)排好,存入一个数组 \(SA[~]\)。其中 \(SA[~i~]=j\) 表示排好序后排名第 \(i\) 的后缀是 后缀 \(j\)。
此外还有一个 \(rank[~]\) 数组。\(rank[~j~]=i\) 表示后缀 \(j\) 排好序后的排名是 \(i\)。
如图1(后缀数组——处理字符串的有力工具 \(by\) 罗穗骞)
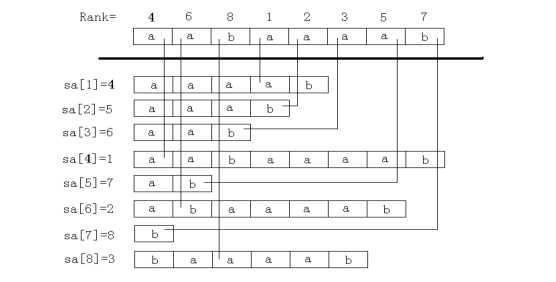
那么,问题来了,如何快速求后缀数组?
倍增法的主要思想是:
每次将所有后缀按照前 \(2^{k}\) 个字符排序,最后得出所有后缀的排序。这样问题就转化为了:现在已知所有后缀关于前 \(2^{k-1}\) 个字符的排序,要对所有后缀排序按前 \(2^k\) 个字符排序。
显然,可以将前 \(2^k\) 个字符分为两部分,每一部分的长度都是 \(2^{k-1}\) ,并且这两部分按照字典序排序后的名次是已知的。
这两部分中,在前面的部分的排名是第一关键字( \(key1\) ),在后面的部分的排名就是第二关键字( \(key2\) )。然后再按照关键字进行排序,更新(\(update\)) \(rank[~]\) 数组,得到新的排名。
如图,字符串“\(aabaaaab\)” 的后缀数组处理(后缀数组——处理字符串的有力工具 \(by\) 罗穗骞)。
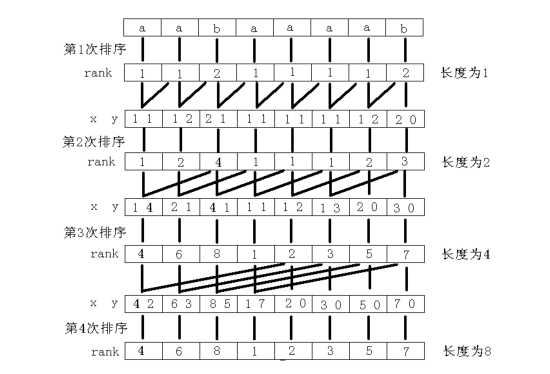
因为字符串的每个后缀都是不同的(起码长度不相同),所以最后得到的 \(rank[~]\) 数组里的数必定是互不相同的。同样,如果再做第 \(k\) 次倍增时,得到的 \(rank[~]\) 数组如果已经互不相同了,那么就说明已经找到了最终的 \(rank[~]\) 数组,可以直接退出循环了。
以上就是 后缀数组-倍增法 的全部流程(个人认为还是很容易理解的,后缀数组的难点应该在基数排序)。下面是完成以上流程的两种排序方法。
快速排序实现的 后缀数组-倍增法 是很直观、容易理解的,有助于初学者更好地理解 后缀数组-倍增法 的思路,编程难度也不是很大,值得一写。
放代码之前,再来温习一下几个数组表示的意义:
\(sa[i]=j\):排名第 \(i\) 的后缀是后缀\(j\)
\(rank[j]=i\):后缀 \(j\) 在所有后缀中排名第 \(i\)
\(key1\):第一关键字(某个子串的前半部分)
\(key2\):第二关键字(某个子串的后半部分)
\(index\):表示后缀\(index\)
然后放代码:
//快排
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
struct node
{
int key1, key2, index;
}data[maxn];
bool cmp(node x,node y)
{
if(x.key1 < y.key1) return true;
if(x.key1 > y.key1) return false;
if(x.key2 < y.key2) return true;
if(x.key2 > y.key2) return false;
return x.index < y.index;
}
char str[maxn];
int n, rank[maxn], sa[maxn];
int main()
{
scanf("%s", str+1);
n = strlen(str+1);
for(int i=1; i<=n; i++) rank[i] = str[i]-‘0‘+1;//预处理长度为 1 的子串的 rank 值
for(int l=1; (1<<l) < n; l++)
{
int len = 1<<(l-1);
//长度为 len/2 的子串已经排好序,存到了rank[]中,现在对长度为 len 的子串排序
for(int i=1; i<=n; i++)
{
data[i].key1 = rank[i], data[i].index = i;
//将长度为 len 的子串分为两部分,前一部分的关键词是key1,用 index 记录这是第几个后缀
if(i+len <= n) data[i].key2 = rank[i+len];//如果该后缀有第二关键字,将其第二关键字存起来
else data[i].key2 = 0;//否则将其第二关键字的优先级赋为最高
}
sort(data+1, data+n+1, cmp);//按照两个关键字从小到大排序
int rk = 1;
rank[data[1].index] = rk;//排在第一个的后缀 rank 值为 1
for(int i=2; i<=n; i++)
{
if(data[i].key1 == data[i-1].key1 and data[i].key2 == data[i-1].key2)//如果当前排名第 i 的后缀与排名为 i-1 的后缀的一、二关键字都相同
rank[data[i].index] = rk;//那么它们的 rank 值也是相同的
else rank[data[i].index] = (++rk);//否则当前的排名第 i 的后缀 rank 值要比前一个高 1
}
if(rk == n) break;//如果当前每个后缀的 rank 值已经不相同了,那么可以直接退出,不必继续循环了
}
for(int i=1; i<=n; i++) sa[rank[i]] = i; //根据 rank[] 数组和 sa[] 数组的关系,可以得到 sa[rank[i]] = i
for(int i=1; i<=n; i++) printf("%d ", sa[i]);
return 0;
}当然,用快速排序来完成倍增法效率是比较低的,大概只能过模板题,遇到大部分的题目都会超时!
于是,基于基数排序的高效倍增法出现啦!!!
\(ps\):个人感觉后缀数组的难点就在这里了。
当然,其实可以直接将 "1.快速排序" 代码中的 “\(sort\)” 直接替换为 "基数排序"。这样子虽然直观,但是常数比较大,在这里不作介绍。
接下来要介绍的是基数排序的一种巧妙的写法,不仅常数小,而且代码短,容易编程实现。但是这种写法理解起来比较困难,理解的时候必须要非常明确每个数组的意思,否则编程的时候很容易出错。
先介绍一下基数排序:
基数排序(\(radix~sort\))属于“分配式排序”(\(distribution~sort\)),又称“桶子法”(\(bucket~sort\))或\(bin ~sort\)。
顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用。
基数排序法是属于稳定性的排序,其时间复杂度为\(\Theta(n\log_rm)\),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。 ——\(by\) 百度百科
拿下面这组数据为例,演示一下基数排序:
\(73, 22, 93, 43, 55, 14, 28, 65, 39, 81\)
首先,从头到尾扫一遍,按照个位数(第二关键字),将这些两位数分配到\(10\)个"桶"里面。如图,
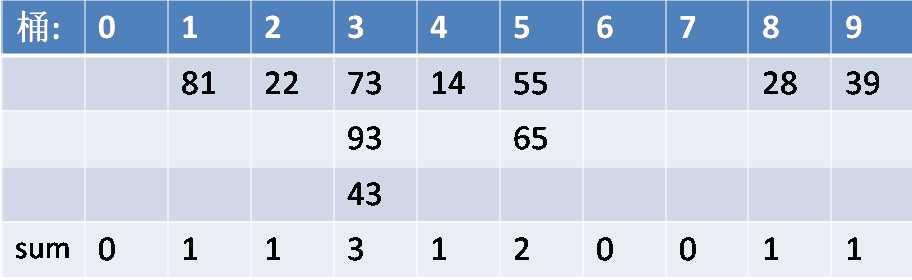
开一个\(sum[~]\)数组,\(sum[i]=j\) 表示个位数(第二关键字)是 \(i\) 的数有 \(j\) 个。
然后将\(sum[~]\)做一个前缀和(别着急,待会就知道\(sum\)数组的作用了)。如图,
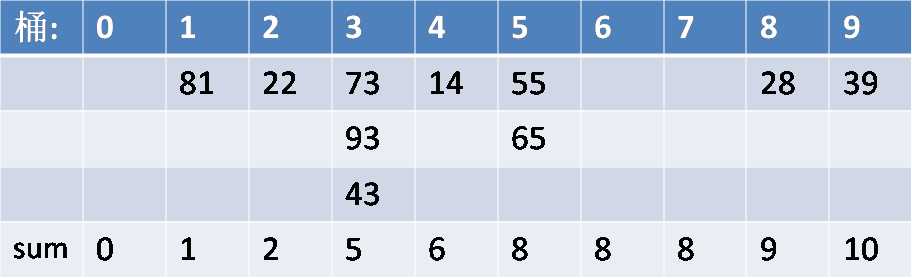
按照基数排序的思想,接下来我们将上图中的序列按照个位数(第二关键字)的大小从小到大取出来(为保证基数排序的稳定性,若第二关键字相同,在数组中存储原序列的下标小的在前),于是形成了如下序列:
$81, 22, 73, 93, 43, 14, 55, 65, 28, 39 $
那么,如何将数据取出来呢?这时,\(sum[~]\) 数组便发挥作用了。
先前我们已经对 \(sum[~]\) 数组做了一次前缀和了,所以此时 \(sum[i]=j\) 的意义就变为了"个位数(第二关键字)小于等于 \(i\) 的数有 \(j\) 个"。
此时,对于每个数,我们都知道“小于等于它的有多少个数”,这个数的位置也就确定了。
为了使排序具有稳定性,我们需要从后往前扫一遍序列,每遇到一个数(假设其第二关键字为 \(i\)),就将其放入新序列的第 \(sum[i]\) 个位置,然后将 \(sum[i]-1\) (因为该数已经找到了在新系列中的位置,若接下来还有第二关键字为 \(i\) 的数,其下表肯定会小于当前的数,所以在新序列中的位置是当前数的前一位)。
这样就可以高效率地求出按照第二关键字排序后得到的新序列了,时间复杂度:\(\Theta(n)\)。上面所举的例子具体演示见基数排序.pptx。
接下来再对新序列按照上文方法对第一关键字(十位数)排序,这样就会得到一个从小到大的序列。
现在再回过头来看后缀数组,其实是对两个关键字排序,按照上述方法排序即可。
有一点不同的是,因为倍增的时候已经将长度为 \(len\) 的关键字排名算出来了,所以第二关键字不需要按照如上方法排序,可以直接利用上一步的排序结果做出来。
因为我们知道,对于每一个后缀,它们都不一定有第二关键字。假设两个后缀的第一关键字相同,如果其中一个子串没有第二关键字,那么该子串的字典序要小于另一个子串。
所以,没有第二关键字的后缀按照第二关键字排序一定会在新序列的最前面。若第二关键字的长度为 \(len\) ,则后缀 $n-len+1 $ 到后缀 \(n\) 都没有第二关键字。直接按照下标的顺序依次排在新序列的最前面即可。
然后,根据上一次算出的长度为 \(len\) 的子串的排名,依次放入新序列即可。注意!!!: 若第二关键字长度为 \(len\) ,则子串 \(1...len,~~2...(len+1),~~3..(len+2),~~...,~~(len-1)...(len+len-2)\) 绝对不是第二关键字。因为若一个后缀有完整的(长度为\(len\))的第二关键字,则其不可能有不完成的(长度小于\(len\))的第一关键字。前面列举的几个子串如果为第二关键字的话,其所在的后缀的第一关键字必然是不完整的。
就这样,不用排序,我们直接利用已知的排名求出了按照第二关键字排序的新序列。然后再用上文提到过的基数排序的方法,排序出第一关键字,即可得到 \(rank[~]\) 数组。
注意:为了代码简洁,效率高一些,代码中排序出来的序列中存储的都是下标,不是数值,所以理解起来可能会有点绕,一定要明确每个数组表示的意义。
再次明确一下每个数组的定义:
\(sa[i] = j\):排名第 \(i\) 的后缀是 后缀\(j\)
\(rank[j]=i\):(上一步)后缀 \(j\) 的排名是 \(i\)
\(newRank[j]=i\):当前后缀\(j\) 的排名是\(i\)(与\(rank[~]\)数组是迭代的关系,可以理解为滚动数组)
\(sum[i]=j\):第一关键字小于等于\(i\) 的有 \(j\) 个
\(key2[i]=j:\)第二关键字排名为\(i\) 的是后缀\(j\)
下面直接上代码(有注释):
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int sa[maxn], rank[maxn], newRank[maxn], sum[maxn], key2[maxn];
int n, m;
char str[maxn];
bool cmp(int a, int b, int l)
{
if(rank[a] != rank[b]) return false;//如果第一关键字不相同,直接返回不相同
if( (a+l > n and b+l <= n) or (a+l <= n and b+l > n) ) return false;//如果第一关键字相同,但是其中只有一个有第二关键字,直接返回不相同
if(a+l > n and b+l > n) return true;//如果第一关键字相同,且都没有第二关键字,返回相同
return rank[a+l] == rank[b+l];//返回第二关键字相不相同
}
int main()
{
scanf("%s", str+1);
n = strlen(str+1);
for(int i=1; i<=n; i++) sum[rank[i] = str[i]]++; //按照字典序初始化排名
m = max(n, 256);
for(int i=1; i<=m; i++) sum[i]+=sum[i-1];//前缀和,此时sum[i]=j表示的是小于等于i的关键字有j个(此时只有一个关键字)
for(int i=n; i>=1; i--) sa[sum[rank[i]]--] = i; //将分好类的原序列放入新序列中
for(int l=1; l<n; l<<=1)//倍增
{
//l表示已知所有后缀按照前l个字符的排名,求所有后缀按照前l*2个字符的排名
int k = 0;
for(int i=n-l+1; i<=n; i++) key2[++k] = i;//如果没有第二关键字,直接放在序列的最前面
for(int i=1; i<=n; i++) if(sa[i] > l) key2[++k] = sa[i]-l;//跳过不合法的第二关键字
//注意,因为存储的是后缀j,所以存的是它的第一个字符的位置,并不是第二关键字的开头位置,因此sa[i]需要减l
for(int i=1; i<=m; i++) sum[i] = 0;//初始化sum数组
for(int i=1; i<=n; i++) sum[rank[i]]++;//分类
for(int i=1; i<=m; i++) sum[i]+=sum[i-1];//前缀和
for(int i=n; i>=1; i--)
{
int j = key2[i];//key2中,后缀已经排好序了,但实际上在rank数组中,存储的还是上一个位置的排名信息,因此要用到更新后的key2数组的信息
sa[sum[rank[j]]--] = j;//从后往前,按照第一关键字分好的类别依次放入新序列中,同时保证了第二关键字小的较前
}
int rk = 1;
newRank[sa[1]] = rk;//计算排名,排序后的第一名的排名为1
for(int i=2; i<=n; i++)
{
if(cmp(sa[i-1], sa[i], l)) newRank[sa[i]] = rk;//如果当前这一名第一和第二关键字与前一名相同,那么它们的排名也是相同的
else newRank[sa[i]] = ++rk;//否则当前排名是前一个排名的后一位
}
for(int i=1; i<=n; i++) rank[i] = newRank[i];//将当前排名覆盖以前的排名
if(rk == n) break;//剪枝
}
for(int i=1; i<=n; i++) printf("%d ",sa[i]);
return 0;
}终于搞掂了,写到整个人都要虚脱了......我...尽力了。
说实话,后缀数组在实际应用中并没有什么卵用,真正的利器是 \(hight\) 数组。
感觉前面讲那么多都是为了这一章做铺垫,然而这一章因为我too lazy,并不想写那么多......
首先讲一下\(height\)数组的定义:
\(height[i]=j:\)表示排名为\(i\) 的后缀和排名为\(i-1\) 的后缀的最长公共前缀的长度为\(j\)
\(H[i]=j:\)表示后缀\(i\)与其比它排名前一名的后缀的最长公共前缀长度为\(j\)
\(H\)数组有一个极其极其重要的性质:
注意:\(H[i]\ge0\)
证明略。
然后按照后缀1 到 后缀\(n\)的顺序,根据以上性质,缩小枚举范围(本来是1...?,现在变为H[i-1]-1...?),得到\(height\)数组。
直接上代码了:
void getHeight()
{
int k = 0;
for(int i=1; i<=n; i++)
{
if(rank[i] == 1) continue;
int j = sa[rank[i]-1];
while(str[j+k] == str[i+k] and j+k<=n and i+k<=n) k++;
height[rank[i]] = k;
if(k != 0) k--;
}
}终于写完了虽然倒数第2章有些敷衍
总之后缀数组在字符串处理中还是非常有用的。后缀数组是字符串处理中非常优秀的数据结构,是一种处理字符串的有力工具,在不同类型的字符串问题中有广泛的应用。我们应该掌握好后缀数组这种数据结构,并且能在不同类型的题目中灵活、高效的运用。
标签:image 后缀 can include 枚举 稳定性 print std 难点
原文地址:https://www.cnblogs.com/GDOI2018/p/10292378.html