标签:递归 inf nbsp style 组成 this 本质 显示 ges
图由边的集合及顶点的集合组成。边是有方向的是有序图(有向图),否则就是无序图(无向图)。图中的一系列顶点构成路径,路径中所有的顶点都由边连接。路径的长度用路径中第一个顶点到最后一个顶点之间边的数量表示。
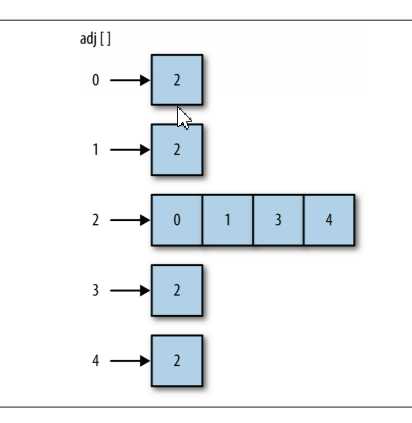
用邻接表来表示边,即将与某一顶点的相邻的边表示为由该顶点的相邻顶点列表构成的数组,并以该顶点作为索引。比如,如果顶点 2 与顶点 0、 1、3、4 相连,那么就将0、1、3、4存储在数组中索引为 2 的位置。
Graph 类定义图
function Graph(v) { this.vertices = v; //顶点的数量 this.edges = 0; this.adj = []; for (var i = 0; i < this.vertices; ++i) { this.adj[i] = []; //保存与顶点 i 相邻的顶点列表 } this.addEdge = addEdge; this.showGraph = showGraph; this.dfs = dfs; this.bfs = bfs; this.marked = []; //保存未访问过的顶点 for (var i = 0; i < this.vertices; ++i) { this.marked[i] = false; } this.pathTo = pathTo; this.hasPathTo = hashPathTo; this.edgeTo = []; }
addEdge(A,B) 添加边,先查找顶点 A 的邻接表,将顶点 B 添加到列表中,然后再查找顶点 B 的邻接表,将顶点 A 加入列表。最后,将边数加 1。
function addEdge(v, w) { this.ajd[v].push(w); this.adj[w].push(v); this.edges++; }
showGraph() 方法显示所有顶点及其相邻顶点列表
function showGraph() { for (var i = 0; i < this.vertices; ++i) { var str = ‘‘; str += i + " -> "; for (var j = 0; j < this.vertices; ++j) { if (this.adj[i][j] != undefined) { str += this.adj[i][j] + ‘ ‘; } } console.log(str); } }
搜索图
确定从一个指定的顶点可以到达其他哪些顶点,有两种搜索方法:深度优先搜索和广度优先搜索。
深度优先搜索从起始顶点开始追溯,直到到达最后一个顶点,然后回溯, 继续追溯下一条路径,直到到达最后的顶点,如此往复,直到没有路径为止。当访问一个没有访问过的顶点时,将它标记为已访问,再递归地去访问在初始顶点的邻接表中其他没有访问过的顶点。
function dfs(v) { this.marked[v] = true; if (this.adj[v] != undefined) { console.log("Visited vertex: " + v); } for(var w of this.adj[v]) { if (!this.marked[w]) { this.dfs(w); } } } //调用 g = new Graph(5); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 3); g.addEdge(2, 4); g.showGraph(); g.dfs(0);
广度优先搜索从第一个顶点开始,尝试访问尽可能靠近它的顶点。本质上,这种搜索是逐层移动的,首先检查最靠近第一个顶点的层,再逐渐向下移动到离起始顶点最远的层。
function bfs(s) { var queue = []; this.marked[s] = true; queue.push(s); // 添加到队尾 while (queue.length > 0) { var v = queue.shift(); // 从队首移除 if (v != undefined) { console.log("Visisted vertex: " + v); } for(var w of this.adj[v]) { if (!this.marked[w]) {this.marked[w] = true; queue.push(w); } } } }
标签:递归 inf nbsp style 组成 this 本质 显示 ges
原文地址:https://www.cnblogs.com/wenxuehai/p/10306688.html