标签:tin oid lag math 情况 技术分享 下标 相互转换 code
一道记忆化搜索题
定义一类行列均单调递增的\(5\times5?\)矩阵,将其展开后所形成的字符串按字典序编号.
题目要求实现编号与字符串的相互转换
? 先不管字符串与编号的相互转换;
? 给你一些限定条件(形如\((x,y)\)处只能填某字符),让你求满足条件的合法矩阵数
? 有两种思路,一种是按顺序搜每一个格子放哪一个字母,另一种是按顺序搜每一个字母放哪一个格子
? 复杂度是\(O(25!)?\),过不了
? 在这里要特别注意第二种思路,记忆化也是在此基础上进行
? 在上面提到的第二种思路进行优化.
? 既然是按照字母顺序依次放到格子里,那么会不会有一些美妙的性质呢?
? 其实是有的,如下图,可有以下性质:
a.已经填进去的数必在一个联通块内.? 显然应如此,否则中间的空肯定填不进更大的字母
b.联通块的轮廓线应是连续下降的折线? 如图,蓝块是已经填好的块
? 假设绿块是我现在要填字母的块,如果填进去后,其上的黄块必定将无字母可填(因为填字母是按顺序填的!)
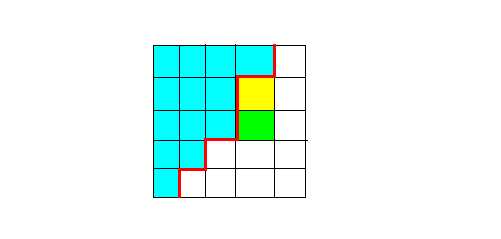
c.合法的联通块内具体的字母顺序不影响剩下的字母填入? 因为以后将要填入的字母必定比现在所有已经填入的字母大,所以相互之间的"影响"是一致的
? 综上所述,我们可以使用记忆化搜索(主要是由于性质c,性质a,b主要是方便设dp状态)
? 设记忆化数组\(f[a][b][c][d][e]\) 表示第1,2,3,4,5行分别填了a,b,c,d,个数的情况下的可能合法矩阵数量,也就求出来求限制条件下的合法矩阵的数量.
? (ps:可以借鉴一下排列的生成算法,感觉本质上差不多QAQ)
? 即通过大家所说的逼近法来实现,
? 现在有一个合法矩阵对应的字符串\(P=p_0p_1p_2...p_{22}p_{23}p_{24}?\),那么它的前面还有多少个满足条件的字符串呢?
? 那么,编号小于\(P\) 的合法矩阵的字符串集合就很明确了,首先将前缀为\(k_0(0<k_0<p_0)\)的串加上,再加上\(k_0k_1(0<k_0<p_0,0<k_1<p_1)\),以此类推,加上\(k_0...k_i(0<k_j<p_j)\)为前缀的字符串即可.
? 再结合我们已经可以较快地求出一定限制条件下的合法矩阵的数量
? 这题就到此终结了.
/*
此题要点:
1.要按字母的顺序来搜
* 2.可以记忆化,用数组f[][][][][]来实现 *
3.有值的f数组的下标a,b,c,d,e应该递减
4.最后用逼近法来完成任务
*/
#include<bits/stdc++.h>
#define il inline
#define R register int
#define ll long long
#define gc getchar
using namespace std;
il int rd()
{
R x=0,flag=1;
char ch=0;
while((ch>'9'||ch<'0')&&ch!='-')ch=gc();
if(ch=='-')flag=-1,ch=gc();
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=gc();
return x*flag;
}
int S[26],ans;
inline bool check(int letter,int pos)
{
return (!S[pos])||(letter==S[pos]);
}
int f[6][6][6][6][6];
bool ok[30];
int dfs(int a,int b,int c,int d,int e,int letter)
{
if(letter>25) return 1;
if(f[a][b][c][d][e]) return f[a][b][c][d][e];
int cnt=0;
if(a<5 && check(letter,a+1)) {cnt+=dfs(a+1,b,c,d,e,letter+1);}
if(b<a && check(letter,b+6)) {cnt+=dfs(a,b+1,c,d,e,letter+1);}
if(c<b && check(letter,c+11)) {cnt+=dfs(a,b,c+1,d,e,letter+1);}
if(d<c && check(letter,d+16)) {cnt+=dfs(a,b,c,d+1,e,letter+1);}
if(e<d && check(letter,e+21)) {cnt+=dfs(a,b,c,d,e+1,letter+1);}
return f[a][b][c][d][e]=cnt;
}
void task1(int num)
{
for(R i=1;i<=25;i++)
{
for(S[i]=1;;S[i]++)
{
if(ok[S[i]])continue;
ok[S[i]]=1;
memset(f,0,sizeof(f));//记得清零
int tmp=dfs(0,0,0,0,0,1);
if(ans+tmp>=num) break;
ans+=tmp;
ok[S[i]]=0;
}
}
for(R i=1;i<=25;i++) cout<<char(S[i]+'A'-1);
}
void task2()
{
string s;
cin>>s;
ans=0;
for(R i=0;i<25;i++)
{
for(S[i+1]=1;S[i+1]<=s[i]-'A';S[i+1]++)
{
if(ok[S[i+1]])continue;
ok[S[i+1]]=1;
memset(f,0,sizeof(f));
ans+=dfs(0,0,0,0,0,1);
ok[S[i+1]]=0;
}
}
cout<<ans+1<<endl;
}
int main ()
{
freopen("twofive.in","r",stdin);
freopen("twofive.out","w",stdout);
char opt;
cin>>opt;
if(opt=='N')task1(rd());
else task2();
//dfs(0,0,0,0,0,1);
//cout<<f[0][0][0][0][0]<<endl;
return 0;
}
?
?
?
标签:tin oid lag math 情况 技术分享 下标 相互转换 code
原文地址:https://www.cnblogs.com/Zenyz/p/10311267.html