树状数组

标签：原码   存储   处理   比较   htm   结构   for   不同   ax1   

首先声明一下，本蒟蒻非常弱qwq，有些地方借鉴了网上的博客，欢迎大家指出错误，下面正式开始讲。

我们为什么要用树状数组

对于普通数组，单点查询非常方便，然鹅有时候对于数组来说，区间的查询就显得力不从心了，这时候就需要用到这种数据结构：树状数组

它可以将一个区间的段和或者最值收集，将原本数组需要的区间查询时间大幅缩减，还有相比较于其它数据结构相对较小的常数，跑的飞起。

原理

那么这种神奇的数据结构原理是什么呢？

我们先来看一张图

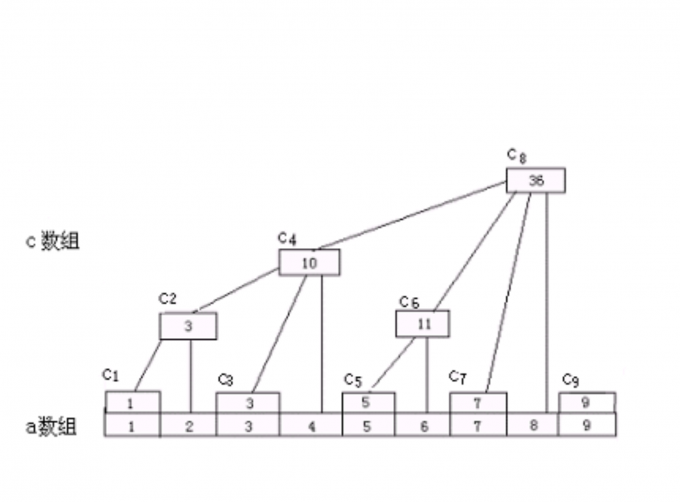
C1 = A1
C2 = A1+A2
C3 = A3
C4 = A1+A2+A3+A4
C5 = A5
C6 = A5+A6
C7 = A7
C8 = A1+A2+A3+A4+A5+A6+A7+A8

emmmmmm 有什么规律，根本看不粗来。

然而我们再细（ting）细（jiao）思（lian）考（jiang）一下

最终我们发现了个神奇的操作lowbit来得出当前位保存的信息，就是它：

int lowbit(int x)
{
    return x&(-x);
}

本质就是将数组当前位的下标转化为2进制码，代表它所存储的数据就是各位二进制数再转化为十进制数下标下的数据的总合（凌乱）

举个栗子，比如说
15=(1111)2，通过lowbit分解，它可以变成4个数的和：

(1111)2=(1)2+(10)2+(100)2+(1000)2

减去15的最小的2的幂次2^0得到14。

减去14的最小的2的幂次2^1得到12。

减去12的最小的2的幂次2^2得到8。

减去8的最小的2的幂次2^3得到0。

从而C(15) = C(14) + C(12) + C(8) + C(0)

只要我们继续层层细分，就可以发现其实它已经包含了它之前所有的信息

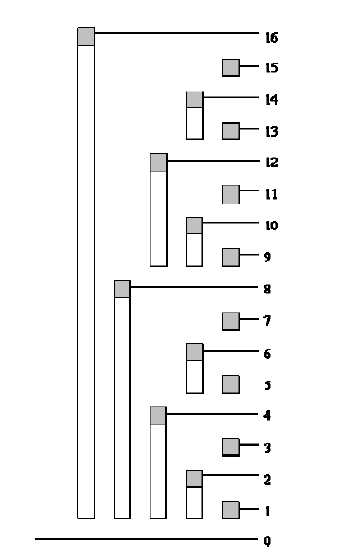
那么为什么x按位与-x就可以取出该数2进制数最低位呢？

这个就运用到了补码的性质，因为补码就是反码加1,进位之后由于加1的作用使其余位的部分与原码相同，而只有lowbit位不同，所以再次按位与之后，所保留下的2进制数位就只有lowbit位了

实际操作

so,进行正式操作，因为树状数组是对一个区间内的数据来进行存储，这样就有了第一个操作，更新数据：

void update(int pos,int num)
{
    for(int i=pos;i<=n;i+=lowb(i))
        c[i]+=num;
}

那么更新完成后就要实现查询了，以下就是查询函数：

int query(int r)
{
    int ans=0;
    for(int i=r;i;i-=lowb(i))
        ans+=c[i];
    return ans;
}

不光可以求区间和，而且只需要一点小小的修改，可以求得区间最值，短小精悍有木有

拓展

多维情况又怎么处理呢？

以二维为例

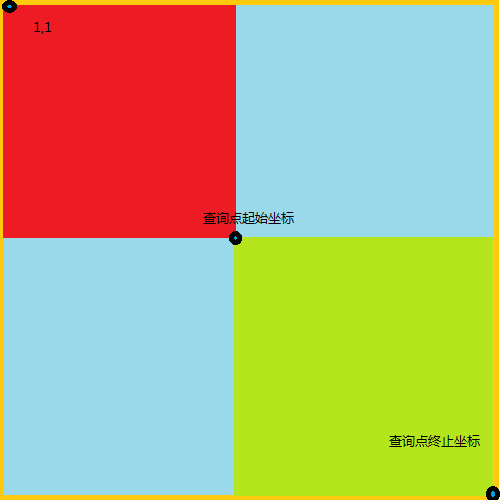
我们要查询一个区间（x1,y1）到(x2,y2) 的区间和只用将(1,1)到(x2,y2)的大区间减去(1,1)到(x1,y2)与(1,1)到(x2,y1)的区间和再加被重复减去的(1,1)到(x1,y1)区间和就可以了

int lowbit(int x){return x&-x;}
void add(int x,int y,int z)
{
    for(int i=x;i<=n;i+=lowbit(i))
        for(int j=y;j<=n;j+=lowbit(j))
            c[i][j]+=z;
}
int quary(int x,int y)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
        for(int j=y;j>0;j-=lowbit(j))
            ans+=c[i][j];
    return ans;
}

......

quary(enda+1,endb+1)-quary(tempa,endb+1)-quary(enda+1,tempb)+quary(tempa,tempb)

不足

树状数组又好写，常数又小，可是，树状数组只能支持单点更新和区间查询，并且求解的问题也比较有限，所以还是要好好学其他数据结构的（才写常数大的一笔的线段树TLE）

改进

针对只能单点更新的树状数组，有这样一个让它超进化改进的方法，就可以让它变得可以进行区间更新

这是一个dalao的博客

我才疏学浅学不来233333

树状数组

标签：原码   存储   处理   比较   htm   结构   for   不同   ax1   

原文地址：https://www.cnblogs.com/superMB/p/10311326.html