标签:效率 span main 计算 out 指针 常数时间 || class
什么是KMP算法:
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。
先来看看暴力解法:
假设主串是目标字符串为S,模式串是待匹配的字符串为P。用暴力算法匹配字符串过程中,我们会把S[0] 跟 P[0] 匹配,如果相同则匹配下一个字符,直到出现不相同的情况,此时我们会丢弃前面的匹配信息,然后把S[1] 跟 P[0]匹配,循环进行,直到主串结束,或者出现匹配成功的情况。这种丢弃前面的匹配信息的方法,极大地降低了匹配效率。时间复杂度O(m*n)
代码:
1 /** 2 * 暴力解法 3 * @param s 主串 4 * @param p 模式串 5 * @return 6 */ 7 private static int indexOf(String s, String p) { 8 int i = 0; 9 int sc = i; 10 int j = 0; 11 while(sc<s.length()){ 12 if (s.charAt(sc)==p.charAt(j)) { 13 sc++; 14 j++; 15 if (j==p.length()) { 16 return i; 17 } 18 }else { 19 i++; 20 sc=i; // 扫描指针以i为起点 21 j=0; // 恢复为0 22 } 23 } 24 return -1; 25 }
而在KMP算法中,对于每一个模式串我们会事先计算出模式串的内部匹配信息,在匹配失败时最大的移动模式串,以减少匹配次数。这样主串的指针就不会回溯了,就能保证一次主串的循环就能解决问题。比如,在简单的一次匹配失败后,我们会想将模式串尽量的右移和主串进行匹配。右移的距离在KMP算法中是如此计算的:在已经匹配的模式串子串中,找出最长的相同的前缀和后缀,然后移动使它们重叠
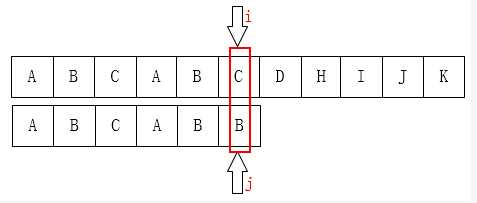
这里可以看出指针指向的地方匹配失败,而在已经匹配的模式串子串"ABCAB"中,最长的相同的前缀和后缀是"AB",长度为2,所以j要向右移动到位置2,因为有相同的前缀和后缀,那么在移动的过程中,这几个字符肯定是能够匹配成功的,就不用去比较了。由此可以得出结论:当匹配失败时,在已经匹配的模式串子串中,如果最前面的k个字符和j之前的最后k个字符是一样的,那么j要移动到下一个位置k。
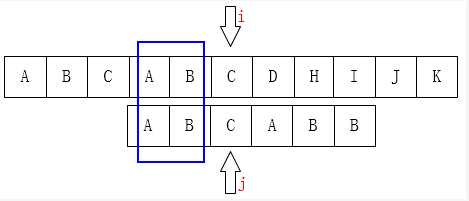
然而,如果每次都要计算最长的相同的前缀反而会浪费时间,所以对于模式串来说,我们会提前计算出每个匹配失败的位置应该移动的距离,花费的时间就成了常数时间。因为在P的每一个位置都可能发生不匹配,也就是说我们要计算每一个位置j对应的k,所以用一个数组next来保存,next[j] = k,表示当S[i] != P[j]时,j指针的下一个位置k。那到底怎么计算next数组呢?
当j为0时,如果这时候不匹配,这种情况,j已经在最左边了,不可能再移动了,next[0] = -1;那么当j为1的时候,如果不匹配,j指针一定是后移到0位置的,因为它前面也就只有这一个位置了,next[1] = 0;如果p[j]==p[k]或者k<0,next[++j] = ++k,否则,k=next[k]。

代码:
1 public static int[] next(String ps) { 2 int pLength = ps.length(); 3 int[] next = new int[pLength + 1]; 4 char[] p = ps.toCharArray(); 5 next[0] = -1; 6 if (ps.length() == 1) 7 return next; 8 next[1] = 0; 9 10 int j = 1; 11 int k = next[j]; //看看位置j的最长匹配前缀在哪里 12 13 while (j < pLength) { 14 //现在要推出next[j+1],检查j和k位置上的关系即可 15 if (k < 0 || p[j] == p[k]) { 16 next[++j] = ++k; 17 } else { 18 k = next[k]; 19 } 20 } 21 return next; 22 }
那么完整的代码就是:
public class KMP { public static void main(String[] args) { String src = "babababcbabababb"; int index = indexOf(src, "bababb"); System.out.println("暴力破解法:"+index); index = indexOf1(src, "bababb"); System.out.println("KMP算法:"+index); } //O(m+n),求count 总共出现了多少次 private static int indexOf1(String s, String p) { if (s.length()==0||p.length()==0) { return -1; } if (p.length()>s.length()) { return -1; } // int count = 0; int []next = next(p); int i = 0;//s位置 int j = 0;//p位置 int sLen = s.length(); int pLen = p.length(); while(i<sLen){ // ①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++ // j=-1,因为next[0]=-1,说明p的第一位和i这个位置无法匹配,这时i,j都增加1,i移位,j从0开始 if (j == -1 || s.charAt(i) == p.charAt(j)) { i++; j++; } else { // ②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j] // next[j]即为j所对应的next值 j = next[j]; } if (j == pLen) {// 匹配成功了 // count++; // j = next[j - 1]; // 上面两行代码是计数模式字符串总共出现了多少次的 return (i - j); } } return -1; // return count; // -1 } public static int[] next(String ps){ int pLength = ps.length(); int []next = new int[pLength+1]; char []p = ps.toCharArray(); next[0] = -1; if (ps.length()==1) { return next; } next[1] = 0; int j = 1; int k = next[j]; // 看看位置j的最长匹配前缀在哪里 while(j<pLength){ // 现在要推出next[j+1],检查j和k位置上的关系即可 if (k<0||p[j]==p[k]) { next[++j] = ++k; }else { k = next[k]; } } return next; } /** * 暴力解法 * @param s 主串 * @param p 模式串 * @return */ private static int indexOf(String s, String p) { int i = 0; int sc = i; int j = 0; while(sc<s.length()){ if (s.charAt(sc)==p.charAt(j)) { sc++; j++; if (j==p.length()) { return i; } }else { i++; sc=i; // 扫描指针以i为起点 j=0; // 恢复为0 } } return -1; } }
结果:
标签:效率 span main 计算 out 指针 常数时间 || class
原文地址:https://www.cnblogs.com/xiaoyh/p/10312194.html