标签:foo 取出 最好 eth gif class 之间 准备 告诉
class ShenXian: # 神仙
def fei(self):
print("神仙都会?")
class Monkey: # 猴
def chitao(self):
print("猴?喜欢吃桃?")
class SunWukong(ShenXian, Monkey): # 孙悟空是神仙, 同时也是?只猴
pass
sxz = SunWukong() # 孙悟空
sxz.chitao() # 会吃桃?
sxz.fei() # 会?
此时, 孙悟空是?只猴?, 同时也是?个神仙. 那孙悟空继承了这两个类. 孙悟空?然就可以执?这两个类中的?法. 多继承?起来简单. 也很好理解. 但是多继承中, 存在着这样?个问题. 当两个?类中出现了重名?法的时候. 这时该怎么办呢? 这时就涉及到如何查找?类?法的这么?个问题.即MRO(method resolution order) 问题. 在python中这是?个很复杂的问题. 因为在不同的python版本中使?的是不同的算法来完成MRO的.
这里需要补充一下python中类的种类(继承需要):
在python2x版本中存在两种类.:
?个叫经典类. 在python2.2之前. ?直使?的是经典类. 经典类在基类的根如果什么都不写.
?个叫新式类. 在python2.2之后出现了新式类. 新式类的特点是基类的根是object类。
python3x版本中只有一种类:
python3中使?的都是新式类. 如果基类谁都不继承. 那这个类会默认继承 object
虽然在python3中已经不存在经典类了. 但是经典类的MRO最好还是学?学. 这是?种树形结构遍历的?个最直接的案例. 在python的继承体系中. 我们可以把类与类继承关系化成?个树形结构的图. 来, 上代码:
 代码示例
代码示例对付这种mro画图就可以:
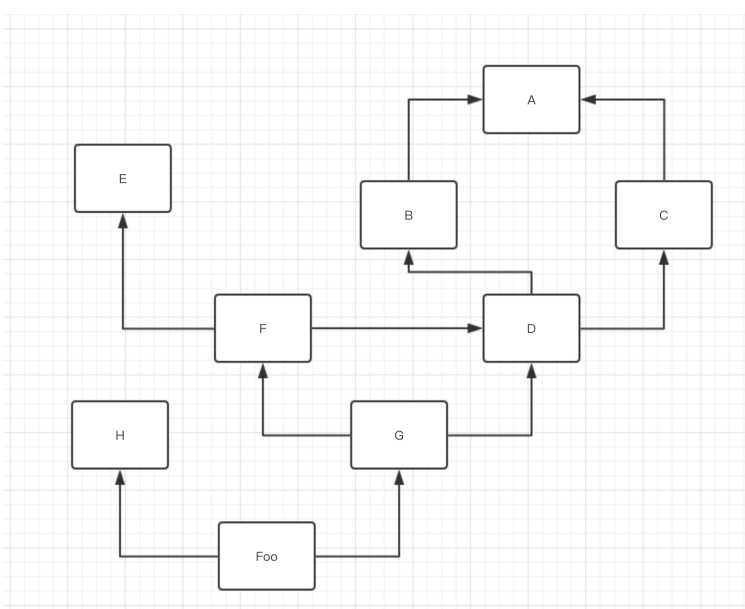
继承关系图已经有了. 那如何进?查找呢? 记住?个原则. 在经典类中采?的是深度优先,遍历?案. 什么是深度优先. 就是?条路走到头. 然后再回来. 继续找下?个.
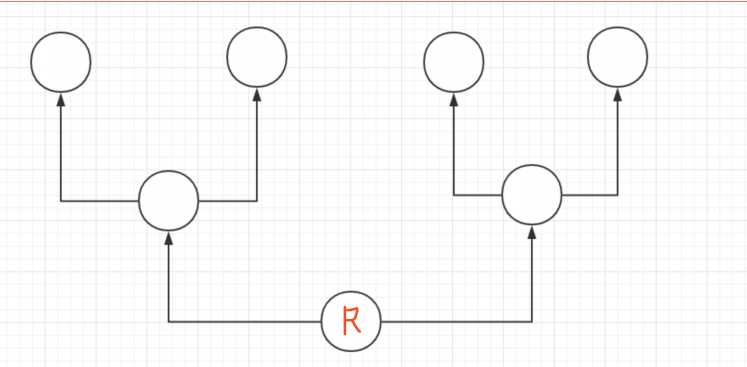
图中每个圈都是准备要送鸡蛋的住址. 箭头和?线表?线路. 那送鸡蛋的顺序告诉你入?在最下?R. 并且必须从左往右送. 那怎么送呢?
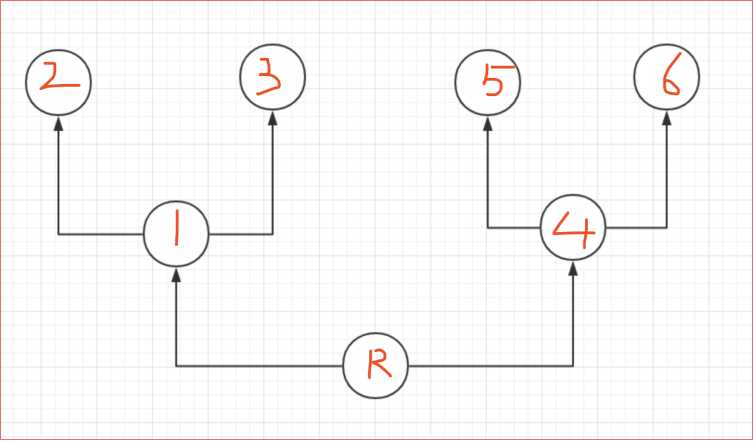
如图. 肯定是按照123456这样的顺序来送. 那这样的顺序就叫深度优先遍历. ?如果是142356呢? 这种被称为?度优先遍历. 好了. 深度优先就说这么多. 那么上?那个图怎么找的呢? MRO是什么呢? 很简单. 记住. 从头开始. 从左往右. ?条路跑到头, 然后回头. 继续?条路跑到头. 就是经典类的MRO算法.
类的MRO: Foo-> H -> G -> F -> E -> D -> B -> A -> C. 你猜对了么?
2.1 mro序列
MRO是一个有序列表L,在类被创建时就计算出来。
通用计算公式为:
mro(Child(Base1,Base2)) = [ Child ] + merge( mro(Base1), mro(Base2), [ Base1, Base2] )
(其中Child继承自Base1, Base2)
如果继承至一个基类:class B(A)
这时B的mro序列为
mro( B ) = mro( B(A) ) = [B] + merge( mro(A) + [A] ) = [B] + merge( [A] + [A] ) = [B,A]
如果继承至多个基类:class B(A1, A2, A3 …)
这时B的mro序列
mro(B) = mro( B(A1, A2, A3 …) ) = [B] + merge( mro(A1), mro(A2), mro(A3) ..., [A1, A2, A3] ) = ...
计算结果为列表,列表中至少有一个元素即类自己,如上述示例[A1,A2,A3]。merge操作是C3算法的核心。
2.2. 表头和表尾
表头:
列表的第一个元素
表尾:
列表中表头以外的元素集合(可以为空)
示例
列表:[A, B, C]
表头是A,表尾是B和C
2.3. 列表之间的+操作
+操作:
[A] + [B] = [A, B]
(以下的计算中默认省略)
---------------------
merge操作示例:
如计算merge( [E,O], [C,E,F,O], [C] ) 有三个列表 : ① ② ③ 1 merge不为空,取出第一个列表列表①的表头E,进行判断 各个列表的表尾分别是[O], [E,F,O],E在这些表尾的集合中,因而跳过当前当前列表 2 取出列表②的表头C,进行判断 C不在各个列表的集合中,因而将C拿出到merge外,并从所有表头删除 merge( [E,O], [C,E,F,O], [C]) = [C] + merge( [E,O], [E,F,O] ) 3 进行下一次新的merge操作 ...... ---------------------
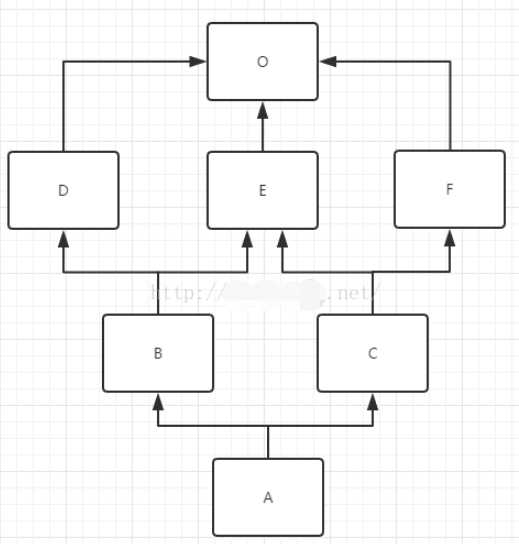
计算mro(A)方式:
mro(A) = mro( A(B,C) )
原式= [A] + merge( mro(B),mro(C),[B,C] )
mro(B) = mro( B(D,E) )
= [B] + merge( mro(D), mro(E), [D,E] ) # 多继承
= [B] + merge( [D,O] , [E,O] , [D,E] ) # 单继承mro(D(O))=[D,O]
= [B,D] + merge( [O] , [E,O] , [E] ) # 拿出并删除D
= [B,D,E] + merge([O] , [O])
= [B,D,E,O]
mro(C) = mro( C(E,F) )
= [C] + merge( mro(E), mro(F), [E,F] )
= [C] + merge( [E,O] , [F,O] , [E,F] )
= [C,E] + merge( [O] , [F,O] , [F] ) # 跳过O,拿出并删除
= [C,E,F] + merge([O] , [O])
= [C,E,F,O]
原式= [A] + merge( [B,D,E,O], [C,E,F,O], [B,C])
= [A,B] + merge( [D,E,O], [C,E,F,O], [C])
= [A,B,D] + merge( [E,O], [C,E,F,O], [C]) # 跳过E
= [A,B,D,C] + merge([E,O], [E,F,O])
= [A,B,D,C,E] + merge([O], [F,O]) # 跳过O
= [A,B,D,C,E,F] + merge([O], [O])
= [A,B,D,C,E,F,O]
---------------------
结果OK. 那既然python提供了. 为什么我们还要如此?烦的计算MRO呢? 因为笔
试.......你在笔试的时候, 是没有电脑的. 所以这个算法要知道. 并且简单的计算要会. 真是项?
开发的时候很少有?这么去写代码.
这个说完了. 那C3到底怎么看更容易呢? 其实很简单. C3是把我们多个类产?的共同继
承留到最后去找. 所以. 我们也可以从图上来看到相关的规律. 这个要?家??多写多画图就
能感觉到了. 但是如果没有所谓的共同继承关系. 那?乎就当成是深度遍历就可以了
标签:foo 取出 最好 eth gif class 之间 准备 告诉
原文地址:https://www.cnblogs.com/YZL2333/p/10324169.html