标签:ima png 3.1 理解 mergesort sso 开始 整数 ogr
整个项目都托管在了 Github 上:https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp
查找更方便的版本见:https://alg4.ikesnowy.com/
这一节内容可能会用到的库文件有 SortApplication,同样在 Github 上可以找到。
善用 Ctrl + F 查找题目。
在下面这段 String 类型的 compareTo() 方法的实现中,第三行对提高运行效率有何帮助?
public int compareTo(String that)
{
if (this == that) return 0; // 这一行
int n = Math.min(this.length(), that.length());
for (int i = 0; i < n; i++)
{
if (this.charAt(i) < that.charAt(i)) return -1;
else if (this.charAt(i) > that.charAt(i)) return +1;
}
return this.length() - that.length();
}如果比较的两个 String 引用的是同一个对象,那么就直接返回相等,不必再逐字符比较。
一个例子:
string s = "abcabc";
string p = s;
Console.WriteLine(s.CompareTo(p));编写一段程序,从标准输入读入一列单词并打印出其中所有由两个单词组成的组合词。
例如,如果输入的单词为 after、thought 和 afterthought,那么 afterthought 就是一个组合词。
将字符串数组 keywords 按照长度排序,于是 keywords[0] 就是最短的字符串。
组合词的最短长度 minLength = 最短字符串的长度 * 2 = keywords[0] * 2。
先找到第一个长度大于等于 minLength 的字符串,下标为 canCombine。
我们从 canCombine 开始,一个个检查是否是组合词。
如果 keywords[canCombine] 是一个组合词,那么它一定是由位于它之前的某两个字符串组合而成的。
组合词的长度一定等于被组合词的长度之和,因此我们可以通过长度快速判断有可能的组合词。
现在题目转化为了如何解决 ThreeSum 问题,即求 a + b = c 型问题,根据 1.4.41 中的解法求解。
keywords[canCombine] 的长度已知,i 从 0 到 canCombine 之间循环,
用二分查找确认 i 到 canCombine 之间有没有符合条件的字符串,注意多个字符串可能长度相等。
using System;
using System.Collections.Generic;
namespace _2._5._2
{
/*
* 2.5.2
*
* 编写一段程序,从标准输入读入一列单词并打印出其中所有由两个单词组成的组合词。
* 例如,如果输入的单词为 after、thought 和 afterthought,
* 那么 afterthought 就是一个组合词。
*
*/
class Program
{
/// <summary>
/// 根据字符串长度进行比较。
/// </summary>
class StringLengthComparer : IComparer<string>
{
public int Compare(string x, string y)
{
return x.Length.CompareTo(y.Length);
}
}
/// <summary>
/// 二分查找,返回符合条件的最小下标。
/// </summary>
/// <param name="keys">搜索范围。</param>
/// <param name="length">搜索目标。</param>
/// <param name="lo">起始下标。</param>
/// <param name="hi">终止下标。</param>
/// <returns></returns>
static int BinarySearch(string[] keys, int length, int lo, int hi)
{
while (lo <= hi)
{
int mid = lo + (hi - lo) / 2;
if (keys[mid].Length == length)
{
while (mid >= lo && keys[mid].Length == length)
mid--;
return mid + 1;
}
else if (length > keys[mid].Length)
lo = mid + 1;
else
hi = mid - 1;
}
return -1;
}
static void Main(string[] args)
{
string[] keywords = Console.ReadLine().Split(‘ ‘);
Array.Sort(keywords, new StringLengthComparer());
int minLength = keywords[0].Length * 2;
// 找到第一个大于 minLength 的字符串
int canCombine = 0;
while (keywords[canCombine].Length < minLength &&
canCombine < keywords.Length)
canCombine++;
// 依次测试是否可能
while (canCombine < keywords.Length)
{
int sum = keywords[canCombine].Length;
for (int i = 0; i < canCombine; i++)
{
int start = BinarySearch(keywords, sum - keywords[i].Length, i, canCombine);
if (start != -1)
{
while (keywords[start].Length + keywords[i].Length == sum)
{
if (keywords[start] + keywords[i] == keywords[canCombine])
Console.WriteLine(keywords[canCombine] + " = " + keywords[start] + " + " + keywords[i]);
else if (keywords[i] + keywords[start] == keywords[canCombine])
Console.WriteLine(keywords[canCombine] + " = " + keywords[i] + " + " + keywords[start]);
start++;
}
}
}
canCombine++;
}
}
}
}找出下面这段账户余额 Balance 类的实现代码的错误。
为什么 compareTo() 方法对 Comparable 接口的实现有缺陷?
public class Balance implements Comparable<Balance>
{
private double amount;
public int compareTo(Banlance that)
{
if (this.amount < that.amount - 0.005) return -1;
if (this.amount > that.amount + 0.005) return +1;
return 0;
}
}这样会破坏相等的传递性。
例如 a = 0.005, b=0.000, c=-0.005,则 a == b, c == b,但是 a != c。
实现一个方法 String[] dedup(String[] a),
返回一个有序的 a[],并删去其中的重复元素。
先排序,然后用书中的代码进行去重。
static string[] Dedup(string[] a)
{
if (a.Length == 0)
return a;
string[] sorted = new string[a.Length];
for (int i = 0; i < a.Length; i++)
{
sorted[i] = a[i];
}
Array.Sort(sorted);
// sorted = sorted.Distinct().ToArray();
string[] distinct = new string[sorted.Length];
distinct[0] = sorted[0];
int j = 1;
for (int i = 1; i < sorted.Length; i++)
{
if (sorted[i].CompareTo(sorted[i - 1]) != 0)
distinct[j++] = sorted[i];
}
return distinct;
}说明为何选择排序是不稳定的?
因为选择排序会交换不相邻的元素。
例如:
B1 B2 A
A B2 B1此时 B1 和 B2 的相对位置被改变,如果将交换限定在相邻元素之间(插入排序)。
B1 B2 A
B1 A B2
A B2 B2此时排序就是稳定的了。
用递归实现 select()。
非递归官网实现见:https://algs4.cs.princeton.edu/23quicksort/QuickPedantic.java.html
原本是和快速排序一块介绍的,将数组重新排列,使得 a[k] 正好是第 k 小的元素,k 从 0 开始。
具体思路类似于二分查找,
先切分,如果切分位置小于 k,那么在右半部分继续切分,否则在左半部分继续切分。
直到切分位置正好等于 k,直接返回 a[k] 。
/// <summary>
/// 使 a[k] 变为第 k 小的数,k 从 0 开始。
/// a[0] ~ a[k-1] 都小于等于 a[k], a[k+1]~a[n-1] 都大于等于 a[k]
/// </summary>
/// <typeparam name="T">元素类型。</typeparam>
/// <param name="a">需要调整的数组。</param>
/// <param name="k">序号。</param>
/// <param name="lo">起始下标。</param>
/// <param name="hi">终止下标。</param>
/// <returns></returns>
static T Select<T>(T[] a, int k, int lo, int hi) where T : IComparable<T>
{
if (k > a.Length || k < 0)
throw new ArgumentOutOfRangeException("select out of bound");
if (lo >= hi)
return a[lo];
int i = Partition(a, lo, hi);
if (i > k)
return Select(a, k, lo, i - 1);
else if (i < k)
return Select(a, k, i + 1, hi);
else
return a[i];
}用 select() 找出 N 个元素中的最小值平均大约需要多少次比较?
参考书中给出的快速排序性能分析方法(中文版 P186,英文版 P293)。
设 $ C_n $ 代表找出 $ n $ 个元素中的最小值所需要的比较次数。
一次切分需要 $ n+1 $ 次比较,下一侧的元素个数从 $ 0 $ 到 $ n-1 $ 都有可能,
于是根据全概率公式,有:
\[
\begin{eqnarray*}
C_n&=&\frac {1}{n} (n+1) +\frac{1}{n} (n+1+C_1)+ \cdots + \frac{1}{n}(n+1+C_{n-1}) \C_n&=&n+1+\frac{1}{n}(C_1+C_2+\cdots+C_{n-1}) \nC_n&=&n(n+1)+(C_1+C_2+\cdots+C_{n-1}) \nC_n-(n-1)C_{n-1}&=&2n+C_{n-1} \nC_n&=&2n+nC_{n-1} \C_n&=&2+C_{n-1} \C_n &=& C_1+2(n-1) \C_n &=& 2n-2 < 2n
\end{eqnarray*}
\]
测试结果符合我们的预期。
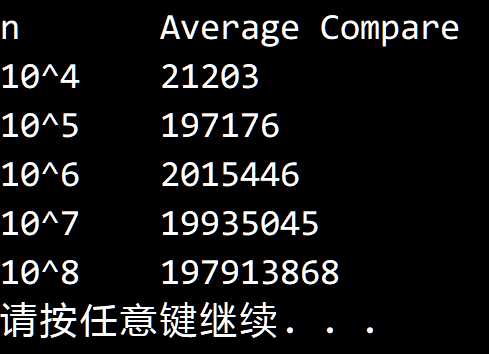
附加:找出第 $ k $ 小的数平均需要的比较次数。
类似的方法也在计算快速排序的平均比较次数时使用,见题 2.3.14。
首先和快速排序类似,select 方法的所有元素比较都发生在切分过程中。
接下来考虑第 $ i $ 小和第 $ j $ 小的元素($ x_i $ ,$ x_j $),
当枢轴选为 $ x_i $ 或 $ x_j $ 时,它们会发生比较;
如果枢轴选为 $ x_i $ 和 $ x_j $ 之间的元素,那么它们会被切分到两侧,不可能发生比较;
如果枢轴选为小于 $ x_i $ 或大于 $ x_j $ 的元素,它们会被切分到同一侧,进入下次切分。
但要注意的是,select 只会对切分的一侧进行再切分,另一侧会被抛弃(快速排序则是两侧都会再切分)。
因此我们需要将第 $ k $ 小的数 $ x_k $ 纳入考虑。
如果 $ x_k>x_j>x_i $ ,且枢轴选了 $ x_k $ 到 $ x_j $ 之间的元素,切分后 $ x_i $ 和 $ x_j $ 会被一起抛弃,不发生比较。
如果 $ x_j > x_k > x_i $ ,枢轴的选择情况和快速排序一致。
如果 $ x_j > x_i > x_k $ ,且枢轴选了 $ x_i $ 到 $ x_k $ 之间的元素,切分后 $ x_i $ 和 $ x_j $ 会被一起抛弃,不发生比较。
综上我们可以得到 $ x_i $ 和 $ x_j $ 之间发生比较的概率 $ \frac{2}{\max(j-i+1, k-i+1,j-k+1)} $ 。
我们利用线性规划的知识把最大值函数的区域画出来,如下图所示:

对蓝色区域积分得:
\[
\begin{eqnarray*}
&&\int_{0}^{k} dj \int_{0}^{j} \frac{2}{j-k+1}\ di \&=& 2 \int_{0}^{k} \frac{j}{j-k+1} \ dj \&<& 2 k
\end{eqnarray*}
\]
对红色区域积分得:
\[
\begin {eqnarray*}
&& \int_{k}^{n} di \int_{i}^{n} \frac{2}{k-i+1} dj \&=& 2\int_{k}^{n} \frac{n-i}{k-i+1} di \&<& 2(n-k)
\end {eqnarray*}
\]
对绿色区域积分得:
\[
\begin{eqnarray*}
&& \int_{0}^{k}di\int_{k}^{n} \frac{2}{j-i+1} dj \&<& \int_{0}^{k}di\int_{k}^{n} \frac{2}{j-i} dj \&=& 2\int_{0}^{k} \ln (n-i) di - 2\int_{0}^{k} \ln(k-i)di \&=& 2i\ln(n-i) \bigg|_{0}^{k} + 2\int_{0}^{k}\frac{i}{n-i} di -
\left[ i\ln(k-i) \bigg|_{0}^{k} + 2\int_{0}^{k} \frac{i}{k-i} di \right] \&=& 2k\ln(n-k)+2\int_{0}^{k}\frac{n}{n-i}-1 \ di -2\int_{0}^{k} \frac{k}{k-i}-1 \ di \&=& 2k\ln(n-k)+2\int_{0}^{k}\frac{n}{n-i} \ di -2k - 2\int_{0}^{k} \frac{k}{k-i} \ di +2k \&=& 2k\ln(n-k) -2n\ln(n-i) \bigg|_{0}^{k} +2k\ln(k-i)\bigg|_{0}^{k} \&=& 2k\ln(n-k)-2n\ln(n-k)+2n\ln n -2k\ln k
\end{eqnarray*}
\]
全部相加得到:
\[
\begin{eqnarray*}
&& 2k+2(n-k)+2k\ln(n-k)-2n\ln(n-k)+2n\ln n -2k\ln k \&=& 2n + 2k\ln(n-k)-2n\ln(n-k)+2n\ln n -2k\ln k \&=& 2n + 2k\ln(n-k)-2n\ln(n-k)+2n\ln n-2k\ln k +2k\ln n-2k\ln n \&=& 2n + 2k\ln n-2k\ln k+2n\ln n-2n\ln(n-k) - 2k\ln n + 2k\ln(n-k) \&=& 2n + 2k\ln \left(\frac{n}{k} \right)+2n\ln\left(\frac{n}{n-k} \right) - 2k\ln\left(\frac{n}{n-k} \right) \&=& 2n+2k\ln\left(\frac{n}{k}\right)+2(n-k)\ln\left(\frac{n}{n-k} \right)
\end{eqnarray*}
\]
于是得到了命题 U 中的结果(中文版 P221,英文版 P347)。
Blum-style analysis of Quickselect
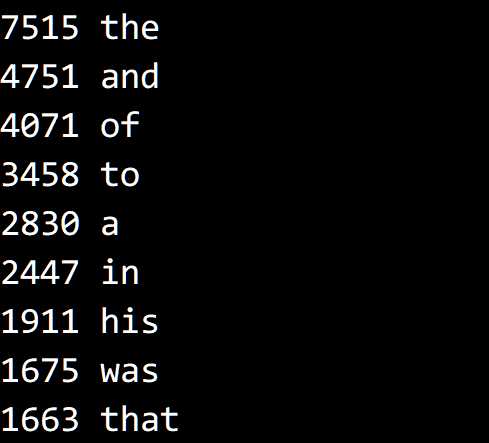
编写一段程序 Frequency,
从标准输入读取一列字符串并按照字符串出现频率由高到低的顺序打印出每个字符串及其出现次数。
官网实现见:https://algs4.cs.princeton.edu/25applications/Frequency.java.html
用到的数据来自(右键另存为):https://introcs.cs.princeton.edu/java/data/tale.txt
先把所有单词读入,然后排序,一样的单词会被放在一起,
接下来遍历一遍记录每个单词出现的次数。
然后按照频率排序,倒序输出即可。
定义了一个嵌套类 Record 来记录单词及出现次数,实现的比较器按照出现次数排序。
class Record : IComparable<Record>
{
public string Key { get; set; } // 单词
public int Value { get; set; } // 频率
public Record(string key, int value)
{
this.Key = key;
this.Value = value;
}
public int CompareTo(Record other)
{
return this.Value.CompareTo(other.Value);
}
}测试结果:
using System;
using System.IO;
namespace _2._5._8
{
class Program
{
class Record : IComparable<Record>
{
public string Key { get; set; } // 单词
public int Value { get; set; } // 频率
public Record(string key, int value)
{
this.Key = key;
this.Value = value;
}
public int CompareTo(Record other)
{
return this.Value.CompareTo(other.Value);
}
}
static void Main(string[] args)
{
string filename = "tale.txt";
StreamReader sr = new StreamReader(File.OpenRead(filename));
string[] a = sr.ReadToEnd().Split(new char[] { ‘ ‘, ‘\n‘, ‘\r‘ }, StringSplitOptions.RemoveEmptyEntries);
Array.Sort(a);
Record[] records = new Record[a.Length];
string word = a[0];
int freq = 1;
int m = 0;
for (int i = 0; i < a.Length; i++)
{
if (!a[i].Equals(word))
{
records[m++] = new Record(word, freq);
word = a[i];
freq = 0;
}
freq++;
}
records[m++] = new Record(word, freq);
Array.Sort(records, 0, m);
// 只显示频率为前 1% 的单词
for (int i = m - 1; i >= m * 0.99; i--)
Console.WriteLine(records[i].Value + " " + records[i].Key);
}
}
}为将右侧所示的数据排序编写一个新的数据类型。
右侧给出的是道琼斯指数,官方数据(右键另存为):DJI
设计一个类保存日期和交易量,然后按照交易量排序即可。
/// <summary>
/// 道琼斯指数。
/// </summary>
class DJIA : IComparable<DJIA>
{
public string Date { get; set; }
public long Volume { get; set; }
public DJIA(string date, long vol)
{
this.Date = date;
this.Volume = vol;
}
public int CompareTo(DJIA other)
{
return this.Volume.CompareTo(other.Volume);
}
}创建一个数据类型 Version 来表示软件的版本,例如 155.1.1、155.10.1、155.10.2。
为它实现 Comparable 接口,其中 115.1.1 的版本低于 115.10.1。
用一个 int 数组来保存版本号,按顺序进行比较。
如果两个版本号不等长且前缀相同,那么较长的版本号比较高,例如:1.2.1 和 1.2。
using System;
namespace _2._5._10
{
/// <summary>
/// 版本号。
/// </summary>
class Version : IComparable<Version>
{
private int[] versionNumber;
public Version(string version)
{
string[] versions = version.Split(‘.‘);
this.versionNumber = new int[versions.Length];
for (int i = 0; i < versions.Length; i++)
{
this.versionNumber[i] = int.Parse(versions[i]);
}
}
public int CompareTo(Version other)
{
for (int i = 0; i < this.versionNumber.Length && i < other.versionNumber.Length; i++)
{
if (this.versionNumber[i].CompareTo(other.versionNumber[i]) != 0)
return this.versionNumber[i].CompareTo(other.versionNumber[i]);
}
return this.versionNumber.Length.CompareTo(other.versionNumber.Length);
}
public override string ToString()
{
string result = "";
for (int i = 0; i < this.versionNumber.Length - 1; i++)
{
result += this.versionNumber[i] + ".";
}
result += this.versionNumber[this.versionNumber.Length - 1].ToString();
return result;
}
}
}描述排序结果的一种方法是创建一个保存 0 到 a.length - 1 的排列 p[],
使得 p[i] 的值为 a[i] 元素的最终位置。
用这种方法描述插入排序、选择排序、希尔排序、归并排序、快速排序和堆排序
对一个含有 7 个相同元素的数组的排序结果。
结果如下,其中快速排序去掉了一开始打乱数组的步骤:
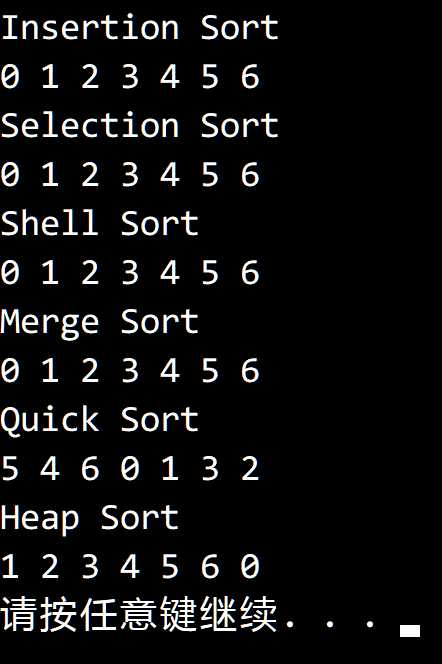
只有快速排序和堆排序会进行交换,剩下四种排序都不会进行交换。
插入排序在排序元素完全相同的数组时只会进行一次遍历,不会交换。
选择排序第 i 次找到的最小值就是 a[i] ,只会让 a[i] 和 a[i] 交换,不会影响顺序。
希尔排序和插入排序类似,每轮排序都不会进行交换。
归并排序是稳定的,就本例而言,只会从左到右依次归并,不会发生顺序变化。
快速排序在遇到相同元素时会交换,因此顺序会发生变化,且每次都是对半切分。
堆排序在删除最大元素时会将第一个元素和最后一个元素交换,使元素顺序发生变化。
using System;
using SortApplication;
namespace _2._5._11
{
class Program
{
/// <summary>
/// 用来排序的元素,记录有自己的初始下标。
/// </summary>
/// <typeparam name="T"></typeparam>
class Item<T> : IComparable<Item<T>> where T : IComparable<T>
{
public int Index;
public T Key;
public Item(int index, T key)
{
this.Index = index;
this.Key = key;
}
public int CompareTo(Item<T> other)
{
return this.Key.CompareTo(other.Key);
}
}
static void Main(string[] args)
{
// 插入排序
Console.WriteLine("Insertion Sort");
Test(new InsertionSort(), 7, 1);
// 选择排序
Console.WriteLine("Selection Sort");
Test(new SelectionSort(), 7, 1);
// 希尔排序
Console.WriteLine("Shell Sort");
Test(new ShellSort(), 7, 1);
// 归并排序
Console.WriteLine("Merge Sort");
Test(new MergeSort(), 7, 1);
// 快速排序
Console.WriteLine("Quick Sort");
QuickSortAnalyze quick = new QuickSortAnalyze
{
NeedShuffle = false,
NeedPath = false
};
Test(quick, 7, 1);
// 堆排序
Console.WriteLine("Heap Sort");
Item<int>[] array = new Item<int>[7];
for (int i = 0; i < 7; i++)
array[i] = new Item<int>(i, 1);
Heap.Sort(array);
for (int i = 0; i < 7; i++)
Console.Write(array[i].Index + " ");
Console.WriteLine();
}
static void Test(BaseSort sort, int n, int constant)
{
Item<int>[] array = new Item<int>[n];
for (int i = 0; i < n; i++)
array[i] = new Item<int>(i, constant);
sort.Sort(array);
for (int i = 0; i < n; i++)
Console.Write(array[i].Index + " ");
Console.WriteLine();
}
}
}调度。
编写一段程序 SPT.java,从标准输入中读取任务的名称和所需的运行时间,
用 2.5.4.3 节所述的最短处理时间优先的原则打印出一份调度计划,使得任务完成的平均时间最小。
官方解答:https://algs4.cs.princeton.edu/25applications/SPT.java.html
把任务按照处理时间升序排序即可。
建立 Job 类,保存任务的名称和处理时间,并实现了 IConparable<Job> 接口。
class Job : IComparable<Job>
{
public string Name;
public double Time;
public Job(string name, double time)
{
this.Name = name;
this.Time = time;
}
public int CompareTo(Job other)
{
return this.Time.CompareTo(other.Time);
}
}using System;
namespace _2._5._12
{
class Program
{
class Job : IComparable<Job>
{
public string Name;
public double Time;
public Job(string name, double time)
{
this.Name = name;
this.Time = time;
}
public int CompareTo(Job other)
{
return this.Time.CompareTo(other.Time);
}
}
static void Main(string[] args)
{
// 官方解答:https://algs4.cs.princeton.edu/25applications/SPT.java.html
int n = int.Parse(Console.ReadLine());
Job[] jobs = new Job[n];
for (int i = 0; i < n; i++)
{
string[] input = Console.ReadLine().Split(‘ ‘);
jobs[i] = new Job(input[0], double.Parse(input[1]));
}
Array.Sort(jobs);
for (int i = 0; i < jobs.Length; i++)
{
Console.WriteLine(jobs[i].Name + " " + jobs[i].Time);
}
}
}
}负载均衡。
编写一段程序 LPT.java,接受一个整数 M 作为命令行参数,
从标准输入中读取任务的名称和所需的运行时间,
用 2.5.4.3 所述的最长处理时间优先原则打印出一份调度计划,
将所有任务分配给 M 个处理器并使得所有任务完成所需的总时间最少。
官方解答见:https://algs4.cs.princeton.edu/25applications/LPT.java.html
使用上题的 Job 类,在本题建立 Processor 类来代表处理器,定义如下:
class Processor : IComparable<Processor>
{
private List<Job> jobs = new List<Job>();
private double busyTime = 0;
public Processor() { }
public void Add(Job job)
{
this.jobs.Add(job);
this.busyTime += job.Time;
}
public int CompareTo(Processor other)
{
return this.busyTime.CompareTo(other.busyTime);
}
public override string ToString()
{
StringBuilder sb = new StringBuilder();
Job[] nowList = this.jobs.ToArray();
for (int i = 0; i < nowList.Length; i++)
{
sb.AppendLine(nowList[i].Name + " " + nowList[i].Time);
}
return sb.ToString();
}
}按照读入所有的任务并排序,再将所有的处理器放进一个最小堆里。
从最小堆取出任务最轻的处理器,按取耗时最长的任务分配给它,再将它放回最小堆中。
最后依次打印处理器的任务分配即可。
using System;
using System.Collections.Generic;
using System.Text;
using SortApplication;
namespace _2._5._13
{
class Program
{
class Job : IComparable<Job>
{
public string Name;
public double Time;
public Job(string name, double time)
{
this.Name = name;
this.Time = time;
}
public int CompareTo(Job other)
{
return this.Time.CompareTo(other.Time);
}
}
class Processor : IComparable<Processor>
{
private List<Job> jobs = new List<Job>();
private double busyTime = 0;
public Processor() { }
public void Add(Job job)
{
this.jobs.Add(job);
this.busyTime += job.Time;
}
public int CompareTo(Processor other)
{
return this.busyTime.CompareTo(other.busyTime);
}
public override string ToString()
{
StringBuilder sb = new StringBuilder();
Job[] nowList = this.jobs.ToArray();
for (int i = 0; i < nowList.Length; i++)
{
sb.AppendLine(nowList[i].Name + " " + nowList[i].Time);
}
return sb.ToString();
}
}
static void Main(string[] args)
{
int processorNum = int.Parse(Console.ReadLine());
int jobNum = int.Parse(Console.ReadLine());
Job[] jobs = new Job[jobNum];
for (int i = 0; i < jobNum; i++)
{
string[] jobDesc = Console.ReadLine().Split(‘ ‘);
jobs[i] = new Job(jobDesc[0], double.Parse(jobDesc[1]));
}
Array.Sort(jobs);
MinPQ<Processor> processors = new MinPQ<Processor>(processorNum);
for (int i = 0; i < processorNum; i++)
{
processors.Insert(new Processor());
}
for (int i = jobs.Length - 1; i >= 0; i--)
{
Processor min = processors.DelMin();
min.Add(jobs[i]);
processors.Insert(min);
}
while (!processors.IsEmpty())
{
Console.WriteLine(processors.DelMin());
}
}
}
}逆域名排序。
为域名编写一个数据类型 Domain 并为它实现一个 compareTo() 方法,使之能够按照逆向的域名排序。
例如,域名 cs.princeton.edu 的逆是 edu.princeton.cs。
这在网络日志处理时很有用。
提示:使用s.split(".") 将域名用点分为若干部分。
编写一个 Domain 的用例,从标准输入读取域名并将他们按照逆域名有序地打印出来。
官方解答:https://algs4.cs.princeton.edu/25applications/Domain.java.html
按照逆域名排序,例如输入的是 com.google 和 com.apple ,
比较的时候是按照 google.com 和 apple.com 进行比较的。
排序结果自然是 apple.com, google.com。
编写的 Domain 类,CompareTo() 中是按照倒序进行比较的。
using System;
using System.Text;
namespace _2._5._14
{
/// <summary>
/// 域名类。
/// </summary>
class Domain : IComparable<Domain>
{
private string[] fields;
private int n;
/// <summary>
/// 构造一个域名。
/// </summary>
/// <param name="url">域名的 url。</param>
public Domain(string url)
{
this.fields = url.Split(‘.‘);
this.n = this.fields.Length;
}
public int CompareTo(Domain other)
{
int minLength = Math.Min(this.n, other.n);
for (int i = 0; i < minLength; i++)
{
int c = this.fields[minLength - i - 1].CompareTo(other.fields[minLength - i - 1]);
if (c != 0)
return c;
}
return this.n.CompareTo(other.n);
}
public override string ToString()
{
StringBuilder sb = new StringBuilder();
for (int i = 0; i < this.fields.Length; i++)
{
if (i != 0)
sb.Append(‘.‘);
sb.Append(this.fields[i]);
}
return sb.ToString();
}
}
}using System;
namespace _2._5._14
{
class Program
{
static void Main(string[] args)
{
Domain[] domains = new Domain[5];
domains[0] = new Domain("edu.princeton.cs");
domains[1] = new Domain("edu.princeton.ee");
domains[2] = new Domain("com.google");
domains[3] = new Domain("edu.princeton");
domains[4] = new Domain("com.apple");
Array.Sort(domains);
for (int i = 0; i < domains.Length; i++)
{
Console.WriteLine(domains[i]);
}
}
}
}垃圾邮件大战。
在非法垃圾邮件之战的伊始,
你有一大串来自各个域名(也就是电子邮件地址中@符号后面的部分)的电子邮件地址。
为了更好的伪造回信地址,你应该总是从相同的域中向目标用户发送邮件。
例如,从 wayne@cs.pinceton.edu 向 rs@cs.princeton.edu 发送垃圾邮件就很不错。
你会如何处理这份电子邮件列表来高效的完成这个任务呢?
利用上一题的逆域名排序将域名相同的电子邮件分在一起。
using System;
namespace _2._5._15
{
class Program
{
static void Main(string[] args)
{
// 利用上一题的逆域名排序,将相同的域名放在一起。
Domain[] emails = new Domain[5];
emails[0] = new Domain("wayne@cs.princeton.edu");
emails[1] = new Domain("windy@apple.com");
emails[2] = new Domain("rs@cs.princeton.edu");
emails[3] = new Domain("ike@ee.princeton.edu");
emails[4] = new Domain("admin@princeton.edu");
Array.Sort(emails);
for (int i = 0; i < emails.Length; i++)
{
Console.WriteLine(emails[i]);
}
}
}
}公正的选举。
为了避免对名字排在字母表靠后的候选人的偏见,
加州在 2003 年的州长选举中将所有候选人按照以下字母顺序排列:
R W Q O J M V A H B S G Z X N T C I E K U P D Y F L。
创建一个遵守这种顺序的数据类型并编写一个用例 California,
在它的静态方法 main() 中将字符串按照这种方式排序。
假设所有字符串都是大写的。
官方解答:https://algs4.cs.princeton.edu/25applications/California.java.html
数据来源:https://introcs.cs.princeton.edu/java/data/california-gov.txt
建立一个 string 的比较器,按照题目给定的顺序比较。
private class CandidateComparer : IComparer<string>
{
private static readonly string order = "RWQOJMVAHBSGZXNTCIEKUPDYFL";
public int Compare(string x, string y)
{
int n = Math.Min(x.Length, y.Length);
for (int i = 0; i < n; i++)
{
int a = order.IndexOf(x[i]);
int b = order.IndexOf(y[i]);
if (a != b)
return a.CompareTo(b);
}
return x.Length.CompareTo(y.Length);
}
}using System;
using System.IO;
using System.Collections.Generic;
namespace _2._5._16
{
class Program
{
// 官方解答:https://algs4.cs.princeton.edu/25applications/California.java.html
private class CandidateComparer : IComparer<string>
{
private static readonly string order = "RWQOJMVAHBSGZXNTCIEKUPDYFL";
public int Compare(string x, string y)
{
int n = Math.Min(x.Length, y.Length);
for (int i = 0; i < n; i++)
{
int a = order.IndexOf(x[i]);
int b = order.IndexOf(y[i]);
if (a != b)
return a.CompareTo(b);
}
return x.Length.CompareTo(y.Length);
}
}
static void Main(string[] args)
{
// 数据来源:https://introcs.cs.princeton.edu/java/data/california-gov.txt
StreamReader sr = new StreamReader(File.OpenRead("california-gov.txt"));
string[] names =
sr.ReadToEnd()
.ToUpper()
.Split
(new char[] { ‘\n‘, ‘\r‘ },
StringSplitOptions.RemoveEmptyEntries);
Array.Sort(names, new CandidateComparer());
for (int i = 0; i < names.Length; i++)
{
Console.WriteLine(names[i]);
}
}
}
}检测稳定性。
扩展练习 2.1.16 中的 check() 方法,对指定数组调用 sort(),
如果排序结果是稳定的则返回 true,否则返回 false。
不要假设 sort() 只会使用 exch() 移动数据。
用一个 Wrapper 类包装准备排序的元素,在排序前同时记录元素的内容和下标。
随后对 Wrapper 数组排序,相同的元素会被放在一起,检查它们的下标是否是递增的。
如果不是递增的,则排序算法就是不稳定的;否则排序算法就有可能是稳定的。
(不稳定的排序算法也可能不改变相同元素的相对位置,比如用选择排序对有序数组排序)
using System;
using SortApplication;
namespace _2._5._17
{
class Program
{
class Wrapper<T> : IComparable<Wrapper<T>> where T : IComparable<T>
{
public int Index;
public T Key;
public Wrapper(int index, T elements)
{
this.Index = index;
this.Key = elements;
}
public int CompareTo(Wrapper<T> other)
{
return this.Key.CompareTo(other.Key);
}
}
static void Main(string[] args)
{
int[] data = new int[] { 7, 7, 4, 8, 8, 5, 1, 7, 7 };
MergeSort merge = new MergeSort();
InsertionSort insertion = new InsertionSort();
ShellSort shell = new ShellSort();
SelectionSort selection = new SelectionSort();
QuickSort quick = new QuickSort();
Console.WriteLine("Merge Sort: " + CheckStability(data, merge));
Console.WriteLine("Insertion Sort: " + CheckStability(data, insertion));
Console.WriteLine("Shell Sort: " + CheckStability(data, shell));
Console.WriteLine("Selection Sort: " + CheckStability(data, selection));
Console.WriteLine("Quick Sort: " + CheckStability(data, quick));
}
static bool CheckStability<T>(T[] data, BaseSort sort) where T : IComparable<T>
{
Wrapper<T>[] items = new Wrapper<T>[data.Length];
for (int i = 0; i < data.Length; i++)
items[i] = new Wrapper<T>(i, data[i]);
sort.Sort(items);
int index = 0;
while (index < data.Length - 1)
{
while (index < data.Length - 1 && items[index].Key.Equals(items[index + 1].Key))
{
if (items[index].Index > items[index + 1].Index)
return false;
index++;
}
index++;
}
return true;
}
}
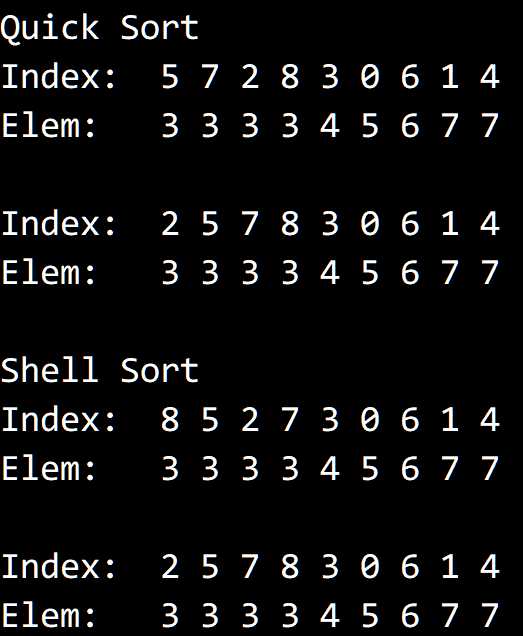
}强制稳定。
编写一段能够将任意排序方法变得稳定的封装代码,
创建一种新的数据类型作为键,将键的原始索引保存在其中,
并在调用 sort() 之后再恢复原始的键。
用和上题一样的 Wrapper 类进行排序。
排序之后,相同的元素会被放在一起,形成一个个子数组。
根据事先保存的原始下标对它们进行排序,即可将不稳定的排序稳定化。
结果:
using System;
using SortApplication;
namespace _2._5._18
{
class Program
{
class Wrapper<T> : IComparable<Wrapper<T>> where T : IComparable<T>
{
public int Index;
public T Key;
public Wrapper(int index, T elements)
{
this.Index = index;
this.Key = elements;
}
public int CompareTo(Wrapper<T> other)
{
return this.Key.CompareTo(other.Key);
}
}
static void Main(string[] args)
{
int[] data = new int[] { 5, 7, 3, 4, 7, 3, 6, 3, 3 };
QuickSort quick = new QuickSort();
ShellSort shell = new ShellSort();
Console.WriteLine("Quick Sort");
Stabilize(data, quick);
Console.WriteLine();
Console.WriteLine("Shell Sort");
Stabilize(data, shell);
}
static void Stabilize<T>(T[] data, BaseSort sort) where T : IComparable<T>
{
Wrapper<T>[] items = new Wrapper<T>[data.Length];
for (int i = 0; i < data.Length; i++)
{
items[i] = new Wrapper<T>(i, data[i]);
}
sort.Sort(items);
Console.Write("Index:\t");
for (int i = 0; i < items.Length; i++)
{
Console.Write(items[i].Index + " ");
}
Console.WriteLine();
Console.Write("Elem:\t");
for (int i = 0; i < items.Length; i++)
{
Console.Write(items[i].Key + " ");
}
Console.WriteLine();
Console.WriteLine();
int index = 0;
while (index < items.Length - 1)
{
while (index < items.Length - 1 &&
items[index].Key.Equals(items[index + 1].Key))
{
// 插入排序
for (int j = index + 1; j > 0 && items[j].Index < items[j - 1].Index; j--)
{
if (!items[j].Key.Equals(items[j - 1].Key))
break;
Wrapper<T> temp = items[j];
items[j] = items[j - 1];
items[j - 1] = temp;
}
index++;
}
index++;
}
Console.Write("Index:\t");
for (int i = 0; i < items.Length; i++)
{
Console.Write(items[i].Index + " ");
}
Console.WriteLine();
Console.Write("Elem:\t");
for (int i = 0; i < items.Length; i++)
{
Console.Write(items[i].Key + " ");
}
Console.WriteLine();
}
}
}Kendall tau 距离。
编写一段程序 KendallTau.java ,
在线性对数时间内计算两组排列之间的 Kendall tau 距离。
官方解答:
Kendall Tau:https://algs4.cs.princeton.edu/25applications/KendallTau.java.html
Inversion:https://algs4.cs.princeton.edu/22mergesort/Inversions.java.html
由书中 2.5.3.2 节得,两个数组之间的 Kendall Tau 距离即为两数组之间顺序不同的数对数目。
如果能够把其中一个数组变成标准排列(即 1,2,3,4... 这样的数组),
那么此时 Kendall Tau 距离就等于另一个数组中的逆序对数量。
现在我们来解决如何把一个数组 a 变成标准排列的方法。
也就是找到函数 $ f(x) ?$,使得 $ f(a[i])=i ?$ ,这样的函数其实就是数组 a 的逆数组。
如下图所示,逆数组 ainv 即为满足 ainv[a[i]] = i 的数组。
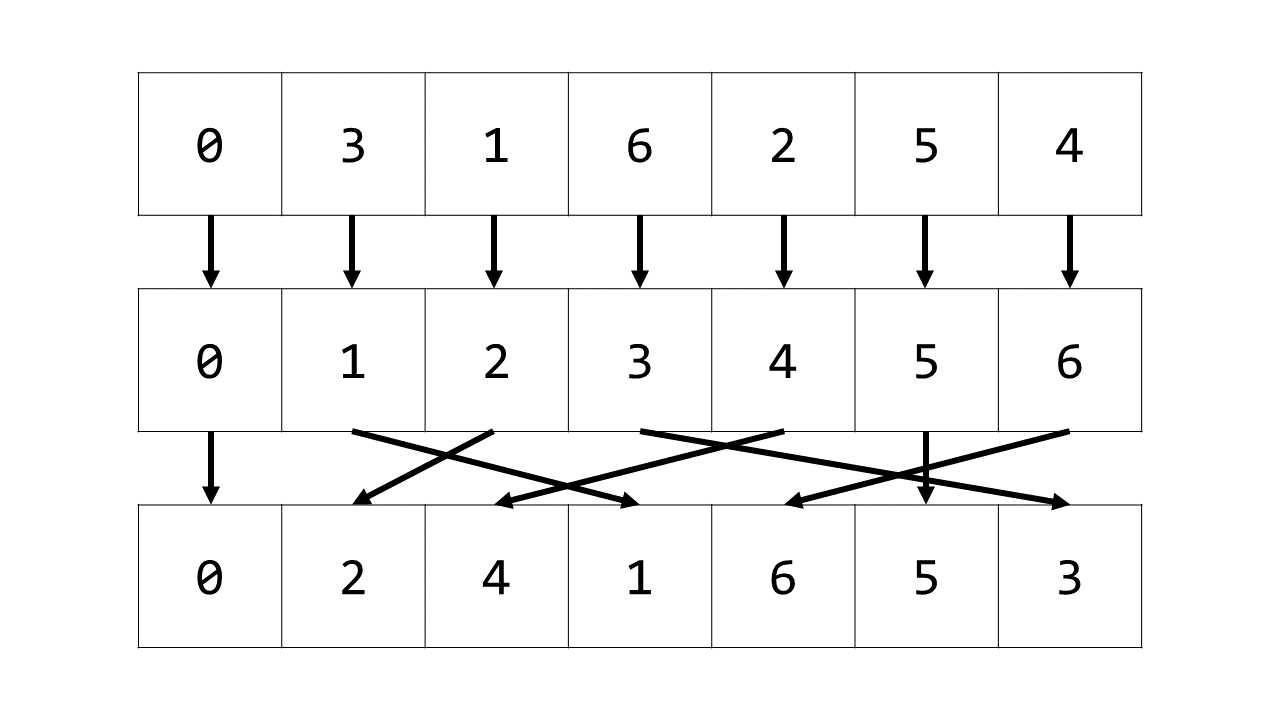
获得逆数组之后,对另一个数组 b 做同样的变换,令数组 bnew[i] = ainv[b[i]] 。
即 ainv[a[i]] = i, ainv[b[i]] = bnew[i] 。
于是问题转化为了 bnew 和标准排列之间的 Kendall Tau 距离,即 bnew 的逆序对数量。
逆序对数量的求法见题 2.2.19。
using System;
namespace _2._5._19
{
class Program
{
static void Main(string[] args)
{
// 官方解答:
// https://algs4.cs.princeton.edu/25applications/KendallTau.java.html
// https://algs4.cs.princeton.edu/22mergesort/Inversions.java.html
int[] testA = { 0, 3, 1, 6, 2, 5, 4 };
int[] testB = { 1, 0, 3, 6, 4, 2, 5 };
Console.WriteLine(Distance(testA, testB));
}
public static long Distance(int[] a, int[] b)
{
if (a.Length != b.Length)
throw new ArgumentException("Array dimensions disagree");
int n = a.Length;
int[] ainv = new int[n];
for (int i = 0; i < n; i++)
{
ainv[a[i]] = i;
}
int[] bnew = new int[n];
for (int i = 0; i < n; i++)
{
bnew[i] = ainv[b[i]];
}
Inversions inversions = new Inversions();
inversions.Count(bnew);
return inversions.Counter;
}
}
}空闲时间。
假设有一台计算机能够并行处理 N 个任务。
编写一段程序并给定一系列任务的起始时间和结束时间,
找出这台机器最长的空闲时间和最长的繁忙时间。
我们按照事件来处理即可,每个事件包含任务名,时间和开始/结束标志。
随后按照时间从小到大排序,遍历数组即可。
设开始的时候机器空闲,设置计数器,作为当前正在运行的任务数量。
如果计数器加一之前计数器为 0,说明空闲状态结束,记录并更新空闲时间,当前时间为忙碌开始的时间。
如果计数器减一之后计数器为 0,说明忙碌状态结束,记录并更新忙碌时间,当前时间为空闲开始的时间。
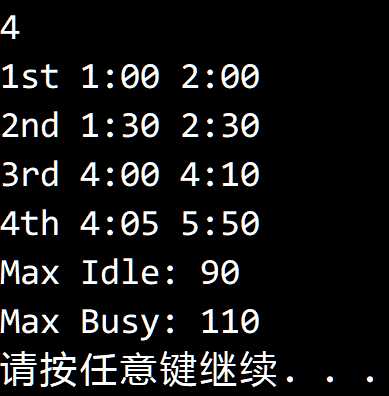
测试结果:
using System;
namespace _2._5._20
{
class Program
{
/// <summary>
/// 任务变化事件。
/// </summary>
class JobEvent : IComparable<JobEvent>
{
public string JobName;
public int Time;
public bool IsFinished = false; // false = 开始,true = 结束
public int CompareTo(JobEvent other)
{
return this.Time.CompareTo(other.Time);
}
}
static void Main(string[] args)
{
// 输入格式: JobName 15:02 17:02
int nowRunning = 0; // 正在运行的程序数量
int maxIdle = 0;
int maxBusy = 0;
int items = int.Parse(Console.ReadLine());
JobEvent[] jobs = new JobEvent[items * 2];
for (int i = 0; i < jobs.Length; i += 2)
{
jobs[i] = new JobEvent();
jobs[i + 1] = new JobEvent();
jobs[i].IsFinished = false; // 开始事件
jobs[i + 1].IsFinished = true; // 停止事件
string[] record = Console.ReadLine().Split(new char[] { ‘ ‘, ‘:‘ }, StringSplitOptions.RemoveEmptyEntries);
jobs[i].JobName = record[0];
jobs[i + 1].JobName = record[0];
jobs[i].Time = int.Parse(record[1]) * 60 + int.Parse(record[2]);
jobs[i + 1].Time = int.Parse(record[3]) * 60 + int.Parse(record[4]);
}
Array.Sort(jobs);
// 事件处理
int idleStart = 0;
int busyStart = 0;
for (int i = 0; i < jobs.Length; i++)
{
// 启动事件
if (!jobs[i].IsFinished)
{
// 空闲状态结束
if (nowRunning == 0)
{
int idle = jobs[i].Time - idleStart;
if (idle > maxIdle)
maxIdle = idle;
// 开始忙碌
busyStart = jobs[i].Time;
}
nowRunning++;
}
else
{
nowRunning--;
// 忙碌状态结束
if (nowRunning == 0)
{
int busy = jobs[i].Time - busyStart;
if (busy > maxBusy)
maxBusy = busy;
// 开始空闲
idleStart = jobs[i].Time;
}
}
}
Console.WriteLine("Max Idle: " + maxIdle);
Console.WriteLine("Max Busy: " + maxBusy);
}
}
}多维排序。
编写一个 Vector 数据类型并将 d 维整型向量排序。
排序方法是先按照一维数字排序,一维数字相同的向量则按照二维数字排序,
再相同的向量则按照三维数字排序,如此这般。
与之前的版本号比较十分类似,对数组进行包装,然后按照次序依次比较即可。
using System;
using System.Text;
namespace _2._5._21
{
class Vector : IComparable<Vector>
{
private int[] data;
public int Length { get; set; }
public Vector(int[] data)
{
this.data = data;
this.Length = data.Length;
}
public int CompareTo(Vector other)
{
int maxN = Math.Max(this.Length, other.Length);
for (int i = 0; i < maxN; i++)
{
int comp = this.data[i].CompareTo(other.data[i]);
if (comp != 0)
return comp;
}
return this.Length.CompareTo(other.Length);
}
public override string ToString()
{
StringBuilder sb = new StringBuilder();
for (int i = 0; i < this.Length; i++)
{
if (i != 0)
sb.Append(‘ ‘);
sb.Append(this.data[i]);
}
return sb.ToString();
}
}
}股票交易。
投资者堆一只股票的买卖交易都发布在电子交易市场中。
他们会指定最高买入价和最低卖出价,以及在该价位买卖的笔数。
编写一段程序,用优先队列来匹配买家和卖家并用模拟数据进行测试。
可以使用两个优先队列,一个用于买家一个用于卖家,
当一方的报价能够和另一方的一份或多份报价匹配时就进行交易。
建立最小堆和最大堆,最小堆保存卖家的报价,最大堆保存买家的报价。
如果最小堆中的最低卖出价低于最大堆的最高买入价,交易达成,交易份额较大的一方需要重新回到堆内。
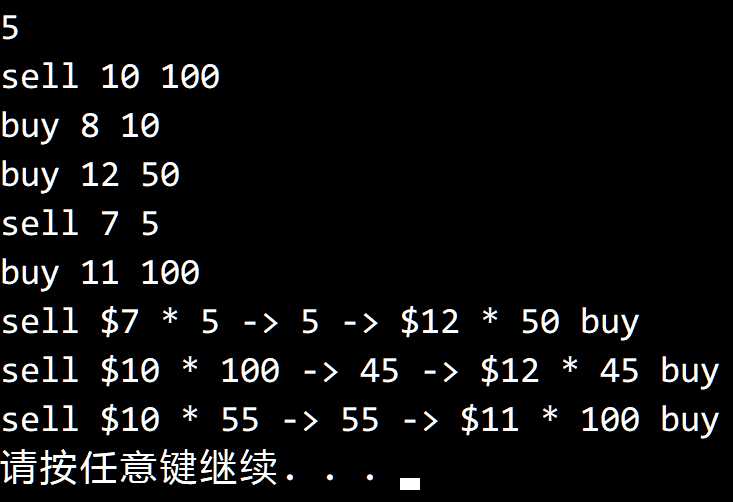
测试结果:
using System;
using SortApplication;
namespace _2._5._22
{
class Program
{
class Ticket : IComparable<Ticket>
{
public double Price;
public int Share;
public int CompareTo(Ticket other)
{
return this.Price.CompareTo(other.Price);
}
}
static void Main(string[] args)
{
// 输入格式: buy 20.05 100
MaxPQ<Ticket> buyer = new MaxPQ<Ticket>();
MinPQ<Ticket> seller = new MinPQ<Ticket>();
int n = int.Parse(Console.ReadLine());
for (int i = 0; i < n; i++)
{
Ticket ticket = new Ticket();
string[] item = Console.ReadLine().Split(‘ ‘);
ticket.Price = double.Parse(item[1]);
ticket.Share = int.Parse(item[2]);
if (item[0] == "buy")
buyer.Insert(ticket);
else
seller.Insert(ticket);
}
while (!buyer.IsEmpty() && !seller.IsEmpty())
{
if (buyer.Max().Price < seller.Min().Price)
break;
Ticket buy = buyer.DelMax();
Ticket sell = seller.DelMin();
Console.Write("sell $" + sell.Price + " * " + sell.Share);
if (buy.Share > sell.Share)
{
Console.WriteLine(" -> " + sell.Share + " -> $" + buy.Price + " * " + buy.Share + " buy");
buy.Share -= sell.Share;
buyer.Insert(buy);
}
else if (buy.Share < sell.Share)
{
sell.Share -= buy.Share;
seller.Insert(sell);
Console.WriteLine(" -> " + buy.Share + " -> $" + buy.Price + " * " + buy.Share + " buy");
}
else
{
Console.WriteLine(" -> " + sell.Share + " -> $" + buy.Price + " * " + buy.Share + " buy");
}
}
}
}
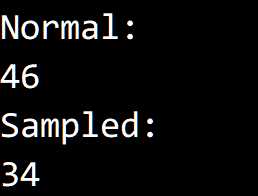
}选择的取样:实验使用取样来改进 select() 函数的想法。
提示:使用中位数可能并不总是有效。
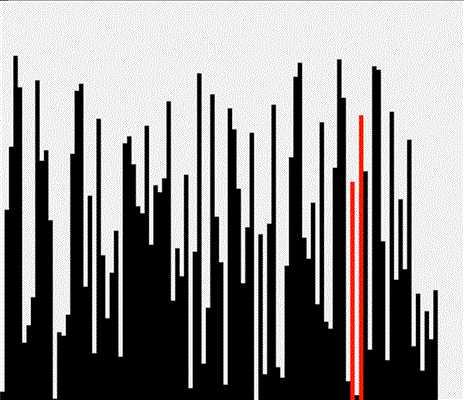
这里我们使用 Floyd-Rivest 算法进行优化,大致思想是:
我们期望第 $ k $ 大的元素位于 a[k] 附近,因此优先对 a[k] 附近的区域进行选择。
每次切分时枢轴都选择 a[k],先递归对样本区域选择,再对整个数组进行选择。
运行示意图:
测试结果:
/// <summary>
/// Floyd–Rivest 方法优化,令 a[k] 变成第 k 小的元素。
/// </summary>
/// <typeparam name="T">元素类型。</typeparam>
/// <param name="a">需要排序的数组。</param>
/// <param name="k">序号</param>
/// <returns></returns>
static T Select<T>(T[] a, int lo, int hi, int k) where T : IComparable<T>
{
if (k < 0 || k > a.Length)
throw new IndexOutOfRangeException("Select elements out of bounds");
while (hi > lo)
{
if (hi - lo > 600)
{
int n = hi - lo + 1;
int i = k - lo + 1;
int z = (int)Math.Log(n);
int s = (int)(Math.Exp(2 * z / 3) / 2);
int sd = (int)Math.Sqrt(z * s * (n - s) / n) * Math.Sign(i - n / 2) / 2;
int newLo = Math.Max(lo, k - i * s / n + sd);
int newHi = Math.Min(hi, k + (n - i) * s / n + sd);
Select(a, newLo, newHi, k);
}
Exch(a, lo, k);
int j = Partition(a, lo, hi);
if (j > k)
hi = j - 1;
else if (j < k)
lo = j + 1;
else
return a[j];
}
return a[lo];
}Floyd–Rivest algorithm - Wikipedia
稳定的优先队列。
实现一个稳定的优先队列(将重复的元素按照它们被插入的顺序返回)。
官方解答:https://algs4.cs.princeton.edu/25applications/StableMinPQ.java.html
在元素插入的同时记录插入顺序,比较的时候把插入顺序也纳入比较。
对于值一样的元素,插入顺序在前的的元素比较小。
交换的时候需要同时交换插入次序。
using System;
using System.Collections;
using System.Collections.Generic;
namespace SortApplication
{
/// <summary>
/// 稳定的最小堆。(数组实现)
/// </summary>
/// <typeparam name="Key">最小堆中保存的元素类型。</typeparam>
public class MinPQStable<Key> : IMinPQ<Key>, IEnumerable<Key> where Key : IComparable<Key>
{
protected Key[] pq; // 保存元素的数组。
protected int n; // 堆中的元素数量。
private long[] time; // 元素的插入次序。
private long timeStamp = 1; // 元素插入次序计数器。
/// <summary>
/// 默认构造函数。
/// </summary>
public MinPQStable() : this(1) { }
/// <summary>
/// 建立指定容量的最小堆。
/// </summary>
/// <param name="capacity">最小堆的容量。</param>
public MinPQStable(int capacity)
{
this.time = new long[capacity + 1];
this.pq = new Key[capacity + 1];
this.n = 0;
}
/// <summary>
/// 删除并返回最小元素。
/// </summary>
/// <returns></returns>
public Key DelMin()
{
if (IsEmpty())
throw new ArgumentOutOfRangeException("Priority Queue Underflow");
Key min = this.pq[1];
Exch(1, this.n--);
Sink(1);
this.pq[this.n + 1] = default(Key);
this.time[this.n + 1] = 0;
if ((this.n > 0) && (this.n == this.pq.Length / 4))
Resize(this.pq.Length / 2);
Debug.Assert(IsMinHeap());
return min;
}
/// <summary>
/// 向堆中插入一个元素。
/// </summary>
/// <param name="v">需要插入的元素。</param>
public void Insert(Key v)
{
if (this.n == this.pq.Length - 1)
Resize(2 * this.pq.Length);
this.pq[++this.n] = v;
this.time[this.n] = ++this.timeStamp;
Swim(this.n);
//Debug.Assert(IsMinHeap());
}
/// <summary>
/// 检查堆是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty() => this.n == 0;
/// <summary>
/// 获得堆中最小元素。
/// </summary>
/// <returns></returns>
public Key Min() => this.pq[1];
/// <summary>
/// 获得堆中元素的数量。
/// </summary>
/// <returns></returns>
public int Size() => this.n;
/// <summary>
/// 获取堆的迭代器,元素以降序排列。
/// </summary>
/// <returns></returns>
public IEnumerator<Key> GetEnumerator()
{
MaxPQ<Key> copy = new MaxPQ<Key>(this.n);
for (int i = 1; i <= this.n; i++)
copy.Insert(this.pq[i]);
while (!copy.IsEmpty())
yield return copy.DelMax(); // 下次迭代的时候从这里继续执行。
}
/// <summary>
/// 获取堆的迭代器,元素以降序排列。
/// </summary>
/// <returns></returns>
IEnumerator IEnumerable.GetEnumerator()
{
return GetEnumerator();
}
/// <summary>
/// 使元素上浮。
/// </summary>
/// <param name="k">需要上浮的元素。</param>
private void Swim(int k)
{
while (k > 1 && Greater(k / 2, k))
{
Exch(k, k / 2);
k /= 2;
}
}
/// <summary>
/// 使元素下沉。
/// </summary>
/// <param name="k">需要下沉的元素。</param>
private void Sink(int k)
{
while (k * 2 <= this.n)
{
int j = 2 * k;
if (j < this.n && Greater(j, j + 1))
j++;
if (!Greater(k, j))
break;
Exch(k, j);
k = j;
}
}
/// <summary>
/// 重新调整堆的大小。
/// </summary>
/// <param name="capacity">调整后的堆大小。</param>
private void Resize(int capacity)
{
Key[] temp = new Key[capacity];
long[] timeTemp = new long[capacity];
for (int i = 1; i <= this.n; i++)
{
temp[i] = this.pq[i];
timeTemp[i] = this.time[i];
}
this.pq = temp;
this.time = timeTemp;
}
/// <summary>
/// 判断堆中某个元素是否大于另一元素。
/// </summary>
/// <param name="i">判断是否较大的元素。</param>
/// <param name="j">判断是否较小的元素。</param>
/// <returns></returns>
private bool Greater(int i, int j)
{
int cmp = this.pq[i].CompareTo(this.pq[j]);
if (cmp == 0)
return this.time[i].CompareTo(this.time[j]) > 0;
return cmp > 0;
}
/// <summary>
/// 交换堆中的两个元素。
/// </summary>
/// <param name="i">要交换的第一个元素下标。</param>
/// <param name="j">要交换的第二个元素下标。</param>
protected virtual void Exch(int i, int j)
{
Key swap = this.pq[i];
this.pq[i] = this.pq[j];
this.pq[j] = swap;
long temp = this.time[i];
this.time[i] = this.time[j];
this.time[j] = temp;
}
/// <summary>
/// 检查当前二叉树是不是一个最小堆。
/// </summary>
/// <returns></returns>
private bool IsMinHeap() => IsMinHeap(1);
/// <summary>
/// 确定以 k 为根节点的二叉树是不是一个最小堆。
/// </summary>
/// <param name="k">需要检查的二叉树根节点。</param>
/// <returns></returns>
private bool IsMinHeap(int k)
{
if (k > this.n)
return true;
int left = 2 * k;
int right = 2 * k + 1;
if (left <= this.n && Greater(k, left))
return false;
if (right <= this.n && Greater(k, right))
return false;
return IsMinHeap(left) && IsMinHeap(right);
}
}
}平面上的点。
为表 1.2.3 的 Point2D 类型编写三个静态的比较器,
一个按照 x 坐标比较,一个按照 y 坐标比较,一个按照点到原点的距离进行比较。
编写两个非静态的比较器,一个按照两点到第三点的距离比较,一个按照两点相对于第三点的辐角比较。
官方解答见:https://algs4.cs.princeton.edu/25applications/Point2D.java.html
这些比较器都以嵌套类的形式在 Point2D 中定义。
静态比较器直接在类中以静态成员的方式声明。
非静态比较器则需要提供工厂方法,该方法新建并返回对应的比较器对象。
/// <summary>
/// 按照 X 顺序比较。
/// </summary>
private class XOrder : Comparer<Point2D>
{
public override int Compare(Point2D x, Point2D y)
{
if (x.X < y.X)
return -1;
if (x.X > y.X)
return 1;
return 0;
}
}
/// <summary>
/// 按照 Y 顺序比较。
/// </summary>
private class YOrder : Comparer<Point2D>
{
public override int Compare(Point2D x, Point2D y)
{
if (x.Y < y.Y)
return -1;
if (x.Y > y.Y)
return 1;
return 0;
}
}
/// <summary>
/// 按照极径顺序比较。
/// </summary>
private class ROrder : Comparer<Point2D>
{
public override int Compare(Point2D x, Point2D y)
{
double delta = (x.X * x.X + x.Y * x.Y) - (y.X * y.X + y.Y * y.Y);
if (delta < 0)
return -1;
if (delta > 0)
return 1;
return 0;
}
}
/// <summary>
/// 按照 atan2 值顺序比较。
/// </summary>
private class Atan2Order : Comparer<Point2D>
{
private Point2D parent;
public Atan2Order() { }
public Atan2Order(Point2D parent)
{
this.parent = parent;
}
public override int Compare(Point2D x, Point2D y)
{
double angle1 = this.parent.AngleTo(x);
double angle2 = this.parent.AngleTo(y);
if (angle1 < angle2)
return -1;
if (angle1 > angle2)
return 1;
return 0;
}
}
/// <summary>
/// 按照极角顺序比较。
/// </summary>
private class PolorOrder : Comparer<Point2D>
{
private Point2D parent;
public PolorOrder() { }
public PolorOrder(Point2D parent)
{
this.parent = parent;
}
public override int Compare(Point2D q1, Point2D q2)
{
double dx1 = q1.X - this.parent.X;
double dy1 = q1.Y - this.parent.Y;
double dx2 = q2.X - this.parent.X;
double dy2 = q2.Y - this.parent.Y;
if (dy2 >= 0 && dy2 < 0)
return -1;
else if (dy2 >= 0 && dy1 < 0)
return 1;
else if (dy1 == 0 && dy2 == 0)
{
if (dx1 >= 0 && dx2 < 0)
return -1;
else if (dx2 >= 0 && dx1 < 0)
return 1;
return 0;
}
else
return -CCW(this.parent, q1, q2);
}
}
/// <summary>
/// 按照距离顺序比较。
/// </summary>
private class DistanceToOrder : Comparer<Point2D>
{
private Point2D parent;
public DistanceToOrder() { }
public DistanceToOrder(Point2D parent)
{
this.parent = parent;
}
public override int Compare(Point2D p, Point2D q)
{
double dist1 = this.parent.DistanceSquareTo(p);
double dist2 = this.parent.DistanceSquareTo(q);
if (dist1 < dist2)
return -1;
else if (dist1 > dist2)
return 1;
else
return 0;
}
}
/// <summary>
/// 提供到当前点极角的比较器。
/// </summary>
/// <returns></returns>
public Comparer<Point2D> Polor_Order()
{
return new PolorOrder(this);
}
/// <summary>
/// 提供到当前点 Atan2 值的比较器。
/// </summary>
/// <returns></returns>
public Comparer<Point2D> Atan2_Order()
{
return new Atan2Order(this);
}
/// <summary>
/// 提供到当前点距离的比较器。
/// </summary>
/// <returns></returns>
public Comparer<Point2D> DistanceTo_Order()
{
return new DistanceToOrder(this);
}简单多边形。
给定平面上的 N 个点,用它们画出一个多边形。
提示:找到 y 坐标最小的点 p,在有多个最小 y 坐标的点时取 x 坐标最小者,
然后将其他点按照以 p 为原点的辐角大小的顺序依次连接起来。
提示中已经给出了方法,使用上一题编写的比较器进行排序即可。
效果演示:

绘图部分代码:
using System.Collections.Generic;
using System.Drawing;
using System.Windows.Forms;
using SortApplication;
namespace _2._5._26
{
public partial class Form2 : Form
{
Graphics panel;
List<Point2D> points;
Point2D startPoint;
double maxX = 0, maxY = 0;
public Form2()
{
InitializeComponent();
}
/// <summary>
/// 显示并初始化绘图窗口。
/// </summary>
public void Init()
{
Show();
this.panel = CreateGraphics();
this.points = new List<Point2D>();
this.startPoint = null;
}
/// <summary>
/// 向画板中添加一个点。
/// </summary>
/// <param name="point"></param>
public void Add(Point2D point)
{
this.points.Add(point);
if (this.startPoint == null)
{
this.startPoint = point;
this.maxX = point.X * 1.1;
this.maxY = point.Y * 1.1;
}
else if (this.startPoint.Y > point.Y)
this.startPoint = point;
else if (this.startPoint.Y == point.Y && this.startPoint.X > point.X)
this.startPoint = point;
if (point.X > this.maxX)
this.maxX = point.X * 1.1;
if (point.Y > this.maxY)
this.maxY = point.Y * 1.1;
this.points.Sort(this.startPoint.Polor_Order());
RefreashPoints();
}
public void RefreashPoints()
{
double unitX = this.ClientRectangle.Width / this.maxX;
double unitY = this.ClientRectangle.Height / this.maxY;
double left = this.ClientRectangle.Left;
double bottom = this.ClientRectangle.Bottom;
this.panel.Clear(this.BackColor);
Pen line = (Pen)Pens.Red.Clone();
line.Width = 6;
Point2D before = this.startPoint;
foreach (var p in this.points)
{
this.panel.FillEllipse(Brushes.Black,
(float)(left + p.X * unitX - 5.0),
(float)(bottom - p.Y * unitY - 5.0),
(float)10.0,
(float)10.0);
this.panel.DrawLine(line,
(float)(left + before.X * unitX),
(float)(bottom - before.Y * unitY),
(float)(left + p.X * unitX),
(float)(bottom - p.Y * unitY));
before = p;
}
this.panel.DrawLine(line,
(float)(left + before.X * unitX),
(float)(bottom - before.Y * unitY),
(float)(left + this.startPoint.X * unitX),
(float)(bottom - this.startPoint.Y * unitY));
}
}
}平行数组的排序。
在将平行数组排序时,可以将索引排序并返回一个 index[] 数组。
为 Insertion 添加一个 indirectSort 方法,接受一个 Comparable 的对象数组 a[] 作为参数,
但它不会将 a[] 中的元素重新排列,而是返回一个整型数组 index[] 使得 a[index[0]] 到 a[index[N-1]] 正好是升序的。
类似于索引排序的做法,访问数组都通过一层索引来间接实现。
首先创建一个数组 index,令 index[i] = i。
排序时的交换变成 index 数组中元素的交换,
读取元素时使用 a[index[i]] 而非 a[i] 。
/// <summary>
/// 间接排序。
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="keys"></param>
/// <returns></returns>
static int[] IndirectSort<T>(T[] keys) where T : IComparable<T>
{
int n = keys.Length;
int[] index = new int[n];
for (int i = 0; i < n; i++)
index[i] = i;
for (int i = 0; i < n; i++)
for (int j = i; j > 0 && keys[index[j]].CompareTo(keys[index[j - 1]]) < 0; j--)
{
int temp = index[j];
index[j] = index[j - 1];
index[j - 1] = temp;
}
return index;
}按文件名排序。
编写一个 FileSorter 程序,从命令行接受一个目录名并打印出按照文件名排序后的所有文件。
提示:使用 File 数据类型。
官方解答:https://algs4.cs.princeton.edu/25applications/FileSorter.java.html
先获得目录里的所有文件名,然后排序输出即可。
using System;
using System.IO;
namespace _2._5._28
{
class Program
{
// 官方解答:https://algs4.cs.princeton.edu/25applications/FileSorter.java.html
static void Main(string[] args)
{
// 输入 ./ 获得当前目录文件。
string directoryName = Console.ReadLine();
if (!Directory.Exists(directoryName))
{
Console.WriteLine(directoryName + " doesn‘t exist or isn‘t a directory");
return;
}
string[] directoryFiles = Directory.GetFiles(directoryName);
Array.Sort(directoryFiles);
for (int i = 0; i < directoryFiles.Length; i++)
Console.WriteLine(directoryFiles[i]);
}
}
}按大小和最后修改日期将文件排序。
为 File 数据类型编写比较器,
使之能够将文件按照大小、文件名或最后修改日期将文件升序或者降序排列。
在程序 LS 中使用这些比较器,它接受一个命令行参数并根据指定的顺序列出目录的内容。
例如,"-t" 指按照时间戳排序。支持多个选项以消除排序位次相同者,同时必须确保排序的稳定性。
首先定义一系列比较器,分别根据文件大小、文件名和最后修改日期比较。
然后修改 Less 的实现,接受一个比较器数组,使用数组中的比较器依次比较,直到比较结果为两者不相同。
最后使用插入排序作为稳定排序,传入比较器数组用于 Less 函数。
using System;
using System.IO;
using System.Collections.Generic;
namespace _2._5._29
{
class Program
{
class FileSizeComparer : Comparer<FileInfo>
{
public override int Compare(FileInfo x, FileInfo y)
{
return x.Length.CompareTo(y.Length);
}
}
class FileNameComparer : Comparer<FileInfo>
{
public override int Compare(FileInfo x, FileInfo y)
{
return x.FullName.CompareTo(y.FullName);
}
}
class FileTimeStampComparer : Comparer<FileInfo>
{
public override int Compare(FileInfo x, FileInfo y)
{
return x.LastWriteTime.CompareTo(y.LastWriteTime);
}
}
static void InsertionSort<T>(T[] keys, Comparer<T>[] comparers)
{
for (int i = 0; i < keys.Length; i++)
for (int j = i; j > 0 && Less(keys, j, j - 1, comparers); j--)
{
T temp = keys[j];
keys[j] = keys[j - 1];
keys[j - 1] = temp;
}
}
static bool Less<T>(T[] keys, int x, int y, Comparer<T>[] comparables)
{
int cmp = 0;
for (int i = 0; i < comparables.Length && cmp == 0; i++)
{
cmp = comparables[i].Compare(keys[x], keys[y]);
}
return cmp < 0;
}
static void Main(string[] args)
{
string[] arguments = Console.ReadLine().Split(‘ ‘);
string directoryPath = arguments[0];
string[] filenames = Directory.GetFiles(directoryPath);
FileInfo[] fileInfos = new FileInfo[filenames.Length];
for (int i = 0; i < filenames.Length; i++)
fileInfos[i] = new FileInfo(filenames[i]);
List<Comparer<FileInfo>> comparers = new List<Comparer<FileInfo>>();
for (int i = 1; i < arguments.Length; i++)
{
string command = arguments[i];
switch (command)
{
case "-t":
comparers.Add(new FileTimeStampComparer());
break;
case "-s":
comparers.Add(new FileSizeComparer());
break;
case "-n":
comparers.Add(new FileNameComparer());
break;
}
}
InsertionSort(fileInfos, comparers.ToArray());
for (int i = 0; i < fileInfos.Length; i++)
{
Console.WriteLine(fileInfos[i].Name + "\t" + fileInfos[i].Length + "\t" + fileInfos[i].LastWriteTime);
}
}
}
}Boerner 定理。
真假判断:如果你先将一个矩阵的每一列排序,
再将矩阵的每一行排序,所有的列仍然是有序的。
证明你的结论。
不妨按照升序排序,$ x_{ij} $ 代表第 $ i $ 行第 $ j $ 列的元素。
首先保证每列都是有序的。
对第一行排序,对于第一行的元素 $ x_{1i} $ ,排序结果无非两种。
要么 $ x_{1i} $ 不改变,要么和更小的元素进行交换。
显然,无论哪种情况,第 $ i $ 列都是有序的。
因此对第一行排序之后,第一行有序,每一列都分别有序。
之后我们对第二行排序,考虑元素 $ x_{11} $。
此时 $ x_{11} $ 小于第一列的所有其他元素,也小于第一行的所有其他元素。
又每一列都分别有序,因此 $ x_{11} $ 是整个矩阵的最小值,第二行不存在比它小的元素。
考虑使用选择排序,我们把第二行的最小值和 $ x_{21} $ 交换,第一列仍然有序。
现在去掉第一列,对剩下的矩阵做一样的操作,可以将第二行依次排序。
同时保证第二行的元素都小于同列的第一行元素。
接下来的行都可以依次类推,最终将整个矩阵的所有行排序,定理得证。
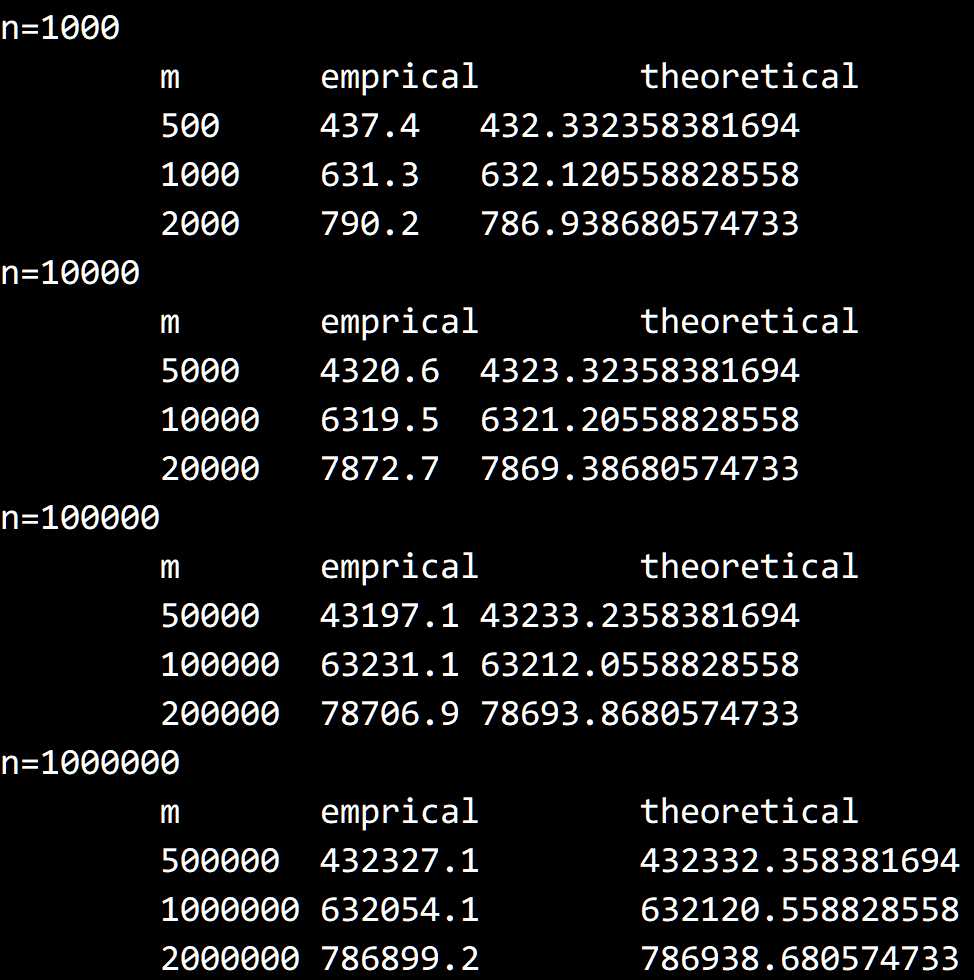
重复元素。
编写一段程序,接受命令行参数 M、N 和 T,
然后使用正文中的代码进行 T 遍实验:
生成 N 个 0 到 M-1 间的 int 值并计算重复值的个数。
令 T=10,N=10^3、10^4、10^5 和 10^6
以及 M = N/2、N 以及 2N。
根据概率论,重复值的个数应该约为 M(1-e^(-α)),其中 α=N/M。
打印一张表格来确认你的实验验证了这个公式。
编写代码进行实验即可,实验结果如下,可以发现十分接近:
using System;
namespace _2._5._31
{
class Program
{
/// <summary>
/// 计算数组中重复元素的个数。
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="a">需要计算重复元素的数组。</param>
/// <returns></returns>
static int Distinct<T>(T[] a) where T : IComparable<T>
{
if (a.Length == 0)
return 0;
Array.Sort(a);
int distinct = 1;
for (int i = 1; i < a.Length; i++)
if (a[i].CompareTo(a[i - 1]) != 0)
distinct++;
return distinct;
}
static void Main(string[] args)
{
int T = 10; // 重复次数
int n = 1000; // 数组初始大小
int nMultipleBy10 = 4; // 数组大小 ×10 的次数
int mMultipleBy2 = 3; // 数据范围 ×2 的次数
Random random = new Random();
for (int i = 0; i < nMultipleBy10; i++)
{
Console.WriteLine("n=" + n);
Console.WriteLine("\tm\temprical\ttheoretical");
int m = n / 2;
for (int j = 0; j < mMultipleBy2; j++)
{
int distinctSum = 0;
for (int k = 0; k < T; k++)
{
int[] data = new int[n];
for (int l = 0; l < n; l++)
data[l] = random.Next(m);
distinctSum += Distinct(data);
}
double empirical = (double)distinctSum / T;
double alpha = (double)n / m;
double theoretical = m * (1 - Math.Exp(-alpha));
Console.WriteLine("\t" + m + "\t" + empirical + "\t" + theoretical);
m *= 2;
}
n *= 10;
}
}
}
}8 字谜题。
8 字谜题是 S.Loyd 于 19 世纪 70 年代发明的一个游戏。
游戏需要一个三乘三的九宫格,其中八格填上了 1 到 8 这 8 个数字,一格空着。
你的目标就是将所有的格子排序。
可以将一个格子向上下或左右(但不能是对角线方向)移动到空白的格子中。
编写一个程序用 A* 算法解决这个问题。
先用到达九宫格的当前位置所需的步数加上错位的格子数量作为优先级函数
(注意,步数至少大于等于错位的格子数)。尝试用其他函数代替错位的格子数量,
比如每个格子距离它的正确位置的曼哈顿距离,
或是这些距离的平方之和。
(前置知识:提前了解 Dijkstra 算法能够降低理解 A* 算法的难度。)
A* 算法是 Dijkstra 算法和最佳优先算法的一种结合。
Dijkstra 算法需要遍历所有结点来找到最短路径,唯一的优化条件就是路径长度。
建立队列 queue ,把所有的结点加入 queue 中;建立数组 d,d[v] 代表起点到点 v 的距离。
开始时只有起点到起点的距离为 0,其他都为无穷大,然后重复如下步骤:
从队列中取出已知距离最短的结点 u,检查该结点的所有边。
如果通过这个点能够以更近的距离到达 v,更新起点到 v 的距离 d[v] = d[u] + distance(u, v)。
等到队列为空之后数组 d 中就存放着起点到其他所有结点的最短距离。
Dijkstra 算法会计算起点到所有点的最短路径,因此会均匀的遍历所有结点,效率较低。
很多时候,我们只需要找到起点到某一终点的最短路径即可,为此遍历整个图显然是不必要的。
通过修改算法,使得比较接近终点的结点优先得到搜索,我们就可能在遍历完全部结点之前获得结果。
在 Dijkstra 算法中,离起点最近的点会被优先搜索,记结点离起点的距离为 g[n] 。
现在引入新的条件,用于估计结点和终点的接近程度,记结点离终点的估计距离为 h[n] 。
令 f[n] = g[n] + h[n],我们按照 f[n] 对等待搜索的结点进行排序。
同时令 h[n] 始终小于 g[n] ,保证离起点的距离 g[n] 权重大于离终点的估计距离 h[n] 。
(h[n]也被称之为容许估计)
于是在离起点距离接近的条件下,离终点比较近的点会被优先搜索,减少搜索范围。
接下来就是算法的具体内容,与 Dijkstra 算法不同,A* 算法不一定需要访问所有结点,
因此 A* 算法需要维护两个集合,openSet 保存等待搜索的结点,closeSet 保存已经搜索过的结点。
和 Dijkstra 算法类似,一开始 openSet 中只有起点,closeSet 则是空的。
然后重复执行如下步骤,直到 openSet 为空:
从 openSet 中取出 f[n] 最小的结点 u ,放入 closeSet。(标记为已访问)
如果 u 就是终点,算法结束。
计算结点 u 直接可达的周围结点,放入集合 neighbors。
遍历 neighbors 中的所有结点 v,做如下判断:
如果 v 已经存在于 closeSet ,忽略之。(防止走回头路)
如果经过 u 不能缩短起点到 v 的路径长度 g[v],忽略之。(和 Dijkstra 算法一样的做法)
否则将 v 放入 openSet,更新 g[v] = g[u] + distance(u, v) ,计算 f[v] = g[v] + h[v]。(更新结点)
以上是 A* 算法的核心逻辑,
为了结合具体问题,我们需要自定义计算 g[n] 和 h[n] 的方法,以及获得某个结点周围结点的方法。
这里有个问题,openSet 和 closeSet 应该用什么数据结构?
closeSet 比较简单,只需要添加和查找即可,哈希表 HashSet 是不二选择。
openSet 需要读取并删除最小元素,以及添加和查找元素,用最小堆 MinPQ 会是比较方便的方法。
书中给出的最小堆 MinPQ 没有实现 Contains 方法,需要自己实现一个,简单顺序查找就够用了。
同时 MinPQ 的 Greater 比较方法也需要重新实现,需要使用基于 f[n] 进行比较的比较器。
现在我们考虑 8 字谜题如何用 A* 算法实现。
棋盘的每一个状态就是一个结点,每走一步就能进入下一个状态,结点可以这么定义:
class SearchNode
{
int[] Board; // 棋盘状态
int Steps; // 已经使用的步数
}g(start, goal) 直接就是 goal.Steps - start.Steps,h(start, goal) 则根据题意有不同的实现。
获得周围结点的方法 GetNeighbors(current),会返回一个数组,其中有从 current 上下左右走获得的棋盘状态。
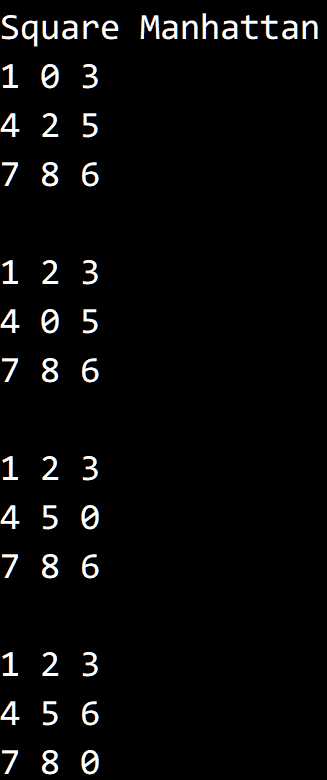
运行结果,初始状态为:
0 1 3
4 2 5
7 9 6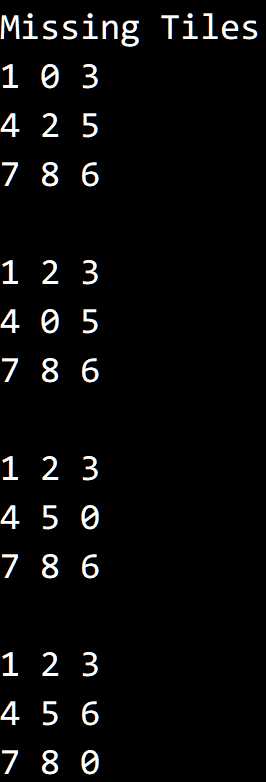

A* 算法的泛型实现
using System;
using System.Collections.Generic;
namespace SortApplication
{
/// <summary>
/// A* 搜索器。
/// </summary>
/// <typeparam name="T"></typeparam>
public abstract class AStar<T> where T : IComparable<T>
{
/// <summary>
/// 相等比较器。
/// </summary>
private readonly IEqualityComparer<T> equalityComparer;
/// <summary>
/// 默认相等比较器。
/// </summary>
class DefaultEqualityComparer : IEqualityComparer<T>
{
public bool Equals(T x, T y)
{
return x.Equals(y);
}
public int GetHashCode(T obj)
{
return obj.GetHashCode();
}
}
/// <summary>
/// 根据 FScore 进行比较的比较器。
/// </summary>
class FScoreComparer : IComparer<T>
{
Dictionary<T, int> fScore;
public FScoreComparer(Dictionary<T, int> fScore)
{
this.fScore = fScore;
}
public int Compare(T x, T y)
{
if (!this.fScore.ContainsKey(x))
this.fScore[x] = int.MaxValue;
if (!this.fScore.ContainsKey(y))
this.fScore[y] = int.MaxValue;
return this.fScore[x].CompareTo(this.fScore[y]);
}
}
/// <summary>
/// 新建一个 Astar 寻路器,使用元素默认相等比较器。
/// </summary>
protected AStar() : this(new DefaultEqualityComparer()) { }
/// <summary>
/// 新建一个 AStar 寻路器。
/// </summary>
/// <param name="equalityComparer">用于确定状态之间相等的比较器。</param>
protected AStar(IEqualityComparer<T> equalityComparer)
{
this.equalityComparer = equalityComparer;
}
/// <summary>
/// 获得最短路径。
/// </summary>
/// <param name="start">起始状态。</param>
/// <param name="goal">终止状态。</param>
/// <returns></returns>
public T[] GetPath(T start, T goal)
{
Dictionary<T, T> comeFrom = new Dictionary<T, T>(this.equalityComparer);
Dictionary<T, int> gScore = new Dictionary<T, int>(this.equalityComparer);
Dictionary<T, int> fScore = new Dictionary<T, int>(this.equalityComparer);
MinPQ<T> openSet = new MinPQ<T>(new FScoreComparer(fScore), this.equalityComparer);
HashSet<T> closeSet = new HashSet<T>(this.equalityComparer);
openSet.Insert(start);
gScore.Add(start, 0);
fScore.Add(start, HeuristicDistance(start, goal));
while (!openSet.IsEmpty())
{
T current = openSet.DelMin();
if (this.equalityComparer.Equals(current, goal))
return ReconstructPath(comeFrom, current);
closeSet.Add(current);
T[] neighbors = GetNeighbors(current);
foreach (T neighbor in neighbors)
{
if (closeSet.Contains(neighbor))
continue;
int gScoreTentative = gScore[current] + ActualDistance(current, neighbor);
// 新状态
if (!openSet.Contains(neighbor))
openSet.Insert(neighbor);
else if (gScoreTentative >= gScore[neighbor])
continue;
// 记录新状态
comeFrom[neighbor] = current;
gScore[neighbor] = gScoreTentative;
fScore[neighbor] = gScore[neighbor] + HeuristicDistance(neighbor, goal);
}
}
return null;
}
/// <summary>
/// 倒回重建最佳路径。
/// </summary>
/// <param name="status">包含所有状态的数组。</param>
/// <param name="from">记载了状态之间顺序的数组。</param>
/// <param name="current">当前状态位置。</param>
/// <returns></returns>
private T[] ReconstructPath(Dictionary<T, T> comeFrom, T current)
{
Stack<T> pathReverse = new Stack<T>();
while (comeFrom.ContainsKey(current))
{
pathReverse.Push(current);
current = comeFrom[current];
}
T[] path = new T[pathReverse.Count];
for (int i = 0; i < path.Length; i++)
{
path[i] = pathReverse.Pop();
}
return path;
}
/// <summary>
/// 计算两个状态之间的估计距离,即 h(n)。
/// </summary>
/// <param name="start">初始状态。</param>
/// <param name="goal">目标状态。</param>
/// <returns></returns>
protected abstract int HeuristicDistance(T start, T goal);
/// <summary>
/// 计算两个状态之间的实际距离,即 g(n)。
/// </summary>
/// <param name="start">初始状态。</param>
/// <param name="goal">目标状态。</param>
/// <returns></returns>
protected abstract int ActualDistance(T start, T goal);
/// <summary>
/// 获得当前状态的周围状态。
/// </summary>
/// <param name="current">当前状态。</param>
/// <returns></returns>
protected abstract T[] GetNeighbors(T current);
}
}A* search algorithm-Wikipedia
SortApplication 库
随机交易。
开发一个接受参数 N 的生成器,
根据你能想到的任意假设条件生成 N 个随机的 Transaction 对象(请见练习 2.1.21 和 2.1.22)。
对于 N=10^3、10^4、10^5 和 10^6,
比较用希尔排序、归并排序、快速排序和堆排序将 N 个交易排序的性能。
编写代码实验即可,结果如下:
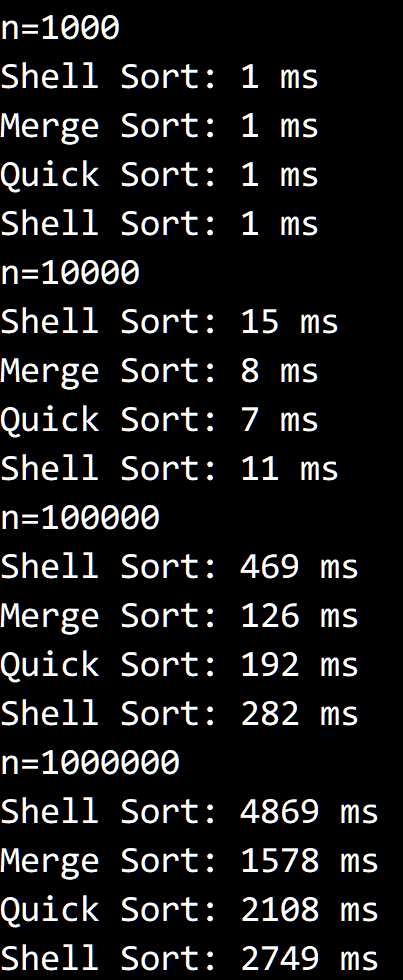
随机交易生成器 TransactionGenerator
using System;
using System.Text;
using SortApplication;
namespace _2._5._33
{
/// <summary>
/// 随机交易生成器。
/// </summary>
class TransactionGenerator
{
private static Random random = new Random();
/// <summary>
/// 生成 n 条随机交易记录。
/// </summary>
/// <param name="n">交易记录的数量。</param>
/// <returns></returns>
public static Transaction[] Generate(int n)
{
Transaction[] trans = new Transaction[n];
for (int i = 0; i < n; i++)
{
trans[i] = new Transaction
(GenerateName(),
GenerateDate(),
random.NextDouble() * 1000);
}
return trans;
}
/// <summary>
/// 获取随机姓名。
/// </summary>
/// <returns></returns>
private static string GenerateName()
{
int nameLength = random.Next(4, 7);
StringBuilder sb = new StringBuilder();
sb.Append(random.Next(‘A‘, ‘Z‘ + 1));
for (int i = 1; i < nameLength; i++)
sb.Append(random.Next(‘a‘, ‘z‘ + 1));
return sb.ToString();
}
/// <summary>
/// 获取随机日期。
/// </summary>
/// <returns></returns>
private static Date GenerateDate()
{
int year = random.Next(2017, 2019);
int month = random.Next(1, 13);
int day;
if (month == 2)
day = random.Next(1, 29);
else if ((month < 8 && month % 2 == 1) ||
(month > 7 && month % 2 == 0))
day = random.Next(1, 32);
else
day = random.Next(1, 31);
Date date = new Date(month, day, year);
return date;
}
}
}标签:ima png 3.1 理解 mergesort sso 开始 整数 ogr
原文地址:https://www.cnblogs.com/ikesnowy/p/10215162.html