标签:就是 参数 小技巧 code 分配 number 中间 技巧 顺序
既然栈是线性表的特例,那么栈的顺序存储其实也是线性表顺序存储的简化,我们简称为顺序栈。线性表是用数组来实现的,对于栈这种只能一头插入删除的线性表来说,用数组哪一端来作为栈顶和栈底比较好?
对,没错,下标为0的一端作为栈底比较好,因为首元素都存在栈底,变化最小,所以让它作栈底。
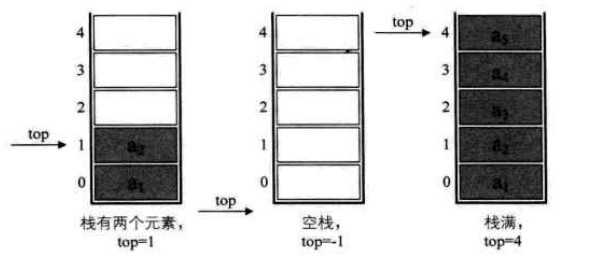
我们定义一个top变量来指示栈顶元素在数组中的位置,这top就如同中学物理学过的游标卡尺的游标,它可以来回移动,意味着栈顶的top可以变大变小,但无论如何游标不能超出尺的长度。同理,若存储栈的长度为StackSize,则栈顶位置top必须小于StackSize。当栈存在一个元素时,top等于0,因此通常把空栈的判定条件定为top等于-1。
来看栈的结构定义:
typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int */
/* 顺序栈结构 */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* 用于栈顶指针 */
}SqStack;若现在有一个栈,StackSize 是5,则栈普通情况、空栈和栈满的情况示意图如下图所示。
进栈的示意图如下:
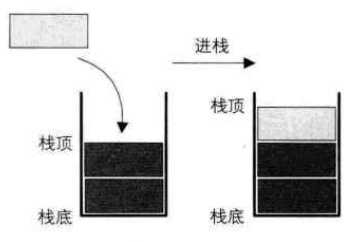
实现进栈只需要两步:
对于进栈操作push,其代码如下:
/* 插入元素e为新的栈顶元素 */
Status Push(SqStack *S,SElemType e)
{
if(S->top == MAXSIZE -1) /* 栈满 */
{
return ERROR;
}
S->top++; /* 栈顶指针增加一 */
S->data[S->top]=e; /* 将新插入元素赋值给栈顶空间 */
return OK;
}出栈的示意图如下:
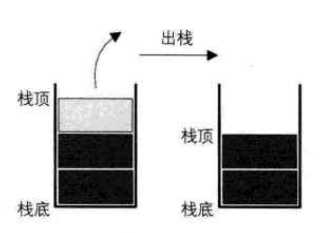
实现出栈也只需要两步:
出栈操作pop,代码如下:
/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */
Status Pop(SqStack *S,SElemType *e)
{
if(S->top==-1)
return ERROR;
*e=S->data[S->top]; /* 将要删除的栈顶元素赋值给e */
S->top--; /* 栈顶指针减一 */
return OK;
}两者没有涉及到任何循环语句,因此时间复杂度均是O(1)。
如果我们有两个相同类型的栈,我们为它们各自开辟了数组空间, 极有可能是第一个栈已经满了,再进栈就溢出了,而另—个栈还有很多存储空间空闲。这又何必呢?我们完全可以用一个数组来存储两个栈,只不过需要点小技巧。
我们的做法如下图所示,数组有两个端点,两个栈有两个栈底,让一个栈的栈底为数组的始端,即下标为0处,另一个栈为数组的末端,即下标为数组长度n-1处。这样,两个栈如果增加元素,就是两端点向中间延伸。
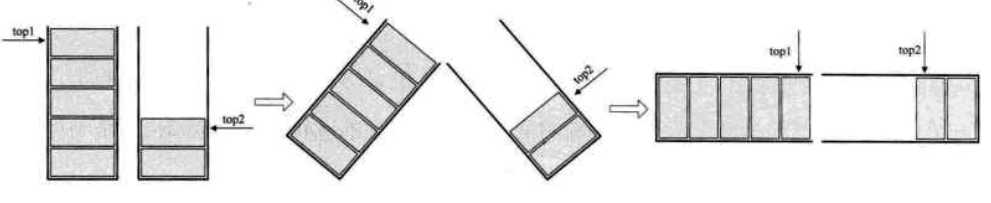
其实关键思路是:它们是在数组的两端,向中间靠拢。top1和top2是栈1和栈2的栈顶指针,可以想象,只要它们俩不见面,两个栈就可以一直使用。从这里也就可以分析出来,栈1为空时,就是top1等于-1时;而当top2等于n时,即是栈2为空时,那什么时候栈满呢?
想想极端的情况,若栈2是空栈,栈1的top1等于n-1时,就是栈1满了。反之,当栈1为空栈时,top2等于0时,为栈2满。但更多的情况就是两个栈见面之时,也就是两个指针之间相差1时,即top1 + 1 == top2为栈满。
两栈共享空间的结构的代码如下:
/* 两栈共享空间结构 */
typedef struct
{
SElemType data[MAXSIZE];
int top1; /* 栈1栈顶指针 */
int top2; /* 栈2栈顶指针 */
}SqDoubleStack;对于两栈共享空间的push方法,我们除了要插入亓素值参数外,还需要有一个判 断是栈1还是栈2的栈号参数stackNumber。插入元素的代码如下:
/* 插入元素e为新的栈顶元素 */
Status Push(SqDoubleStack *S,SElemType e,int stackNumber)
{
if (S->top1+1==S->top2) /* 栈已满,不能再push新元素了 */
return ERROR;
if (stackNumber==1) /* 栈1有元素进栈 */
S->data[++S->top1]=e; /* 若是栈1则先top1+1后给数组元素赋值。 */
else if (stackNumber==2) /* 栈2有元素进栈 */
S->data[--S->top2]=e; /* 若是栈2则先top2-1后给数组元素赋值。 */
return OK;
}因为在开始已经判断了是否有栈满的情况,所以后面的top1+1或top2-1是不担心溢出问题的。
对于两栈共享空间的pop方法,参数就只是判断栈1栈2的参数stackNumber,代码如下:
/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */
Status Pop(SqDoubleStack *S,SElemType *e,int stackNumber)
{
if (stackNumber==1)
{
if (S->top1==-1)
return ERROR; /* 说明栈1已经是空栈,溢出 */
*e=S->data[S->top1--]; /* 将栈1的栈顶元素出栈 */
}
else if (stackNumber==2)
{
if (S->top2==MAXSIZE)
return ERROR; /* 说明栈2已经是空栈,溢出 */
*e=S->data[S->top2++]; /* 将栈2的栈顶元素出栈 */
}
return OK;
}事实上,使用这样的数据结构,通常都是当两个栈的空间需求有相反关系时,也就是一个栈增长时另一个栈在缩短的情况。就像买卖股票—样,你买入时,—定是有一个你不知道的人在做卖出操作。这样使用两栈共享空间存储方法才有比较大的意义,否则两个栈都在不停地增长,那很快就会因栈满而溢出了。
当然,这只是针对两个具有相同数据类型的栈的—个设计上的技巧,如果是不相同数据类型的栈,这种办法不但不能更好地处理问题,反而会使问题变得更复杂,大家要注意这个前提。
#include "stdafx.h"
#include "stdlib.h"
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;
typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int */
/* 顺序栈结构 */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* 用于栈顶指针 */
}SqStack;
Status visit(SElemType c)
{
printf("%d ", c);
return TRUE;
}
/* 构造一个空栈S */
Status InitStack(SqStack *S)
{
/* S.data=(SElemType *)malloc(MAXSIZE*sizeof(SElemType)); */
S->top = -1;
return TRUE;
}
/* 把S置为空栈 */
Status ClearStack(SqStack *S)
{
S->top = -1;
return TRUE;
}
/* 若栈S为空栈,则返回TRUE,否则返回FALSE */
Status StackEmpty(SqStack S)
{
if (S.top == -1)
return TRUE;
else
return FALSE;
}
/* 返回S的元素个数,即栈的长度 */
int StackLength(SqStack S)
{
return S.top + 1;
}
/* 若栈不空,则用e返回S的栈顶元素,并返回TRUE;否则返回FALSE */
Status GetTop(SqStack S, SElemType *e)
{
if (S.top == -1)
return FALSE;
else
*e = S.data[S.top];
return TRUE;
}
/* 插入元素e为新的栈顶元素 */
Status Push(SqStack *S, SElemType e)
{
if (S->top == MAXSIZE - 1) /* 栈满 */
{
return FALSE;
}
S->top++; /* 栈顶指针增加一 */
S->data[S->top] = e; /* 将新插入元素赋值给栈顶空间 */
return TRUE;
}
/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回TRUE;否则返回FALSE */
Status Pop(SqStack *S, SElemType *e)
{
if (S->top == -1)
return FALSE;
*e = S->data[S->top]; /* 将要删除的栈顶元素赋值给e */
S->top--; /* 栈顶指针减一 */
return TRUE;
}
/* 从栈底到栈顶依次对栈中每个元素显示 */
Status StackTraverse(SqStack S)
{
int i;
i = 0;
while (i <= S.top)
{
visit(S.data[i++]);
}
printf("\n");
return TRUE;
}
int main()
{
int j;
SqStack s;
int e;
if (InitStack(&s) == TRUE)
for (j = 1; j <= 10; j++)
Push(&s, j);
printf("栈中元素依次为:");
StackTraverse(s);
Pop(&s, &e);
printf("弹出的栈顶元素 e=%d\n", e);
printf("栈空否:%d(1:空 0:否)\n", StackEmpty(s));
GetTop(s, &e);
printf("栈顶元素 e=%d 栈的长度为%d\n", e, StackLength(s));
ClearStack(&s);
printf("清空栈后,栈空否:%d(1:空 0:否)\n", StackEmpty(s));
return 0;
}
/*
输出结果:
栈中元素依次为:1 2 3 4 5 6 7 8 9 10
弹出的栈顶元素 e=10
栈空否:0(1:空 0:否)
栈顶元素 e=9 栈的长度为9
清空栈后,栈空否:1(1:空 0:否)
*/标签:就是 参数 小技巧 code 分配 number 中间 技巧 顺序
原文地址:https://www.cnblogs.com/linuxAndMcu/p/10327771.html