标签:one 交换 aik 序列 增量排序 选择 归并 quic sorted
一个排序算法可视化的软件,很魔性。
链接:https://pan.baidu.com/s/1hCoMku7UL7IN4hIdYTsuJg 提取码:4y4v
1.冒泡排序

void bubbleSort(int *a, int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n - i; j++) { if (a[j - 1] > a[j]) swap(a[j - 1], a[j]); } } }
2.选择排序

void selectSort(int *a, int length) { for (int i = 0; i < length; i ++) { int minIndex = i; for (int j = i + 1; j < length; j++) { minIndex = a[j] < a[minIndex] ? j : minIndex; } swap(a[i], a[minIndex]); } }
3.插入排序
插入排序在数组近乎于有序的时候,比O(nlogn)的排序是还要快。

void insertSort(int *a, int length) { for (int i = 1; i < length; i++) { int j, temp = a[i]; for (j = i; temp < a[j-1] && j>0; j--) { a[j] = a[j-1]; } a[j] = temp; } }
4.希尔排序(特殊插入排序)
间隔序列的取法有各种方案。最初shell提出取t/2向下取整,直到t=1。但由于直到最后一步,在奇数位置的元素才会与偶数位置的元素进行比较,这样使用这个序列的效率会很低。不同的序列会使希尔排序算法的性能有很大的差异。 至今为止还没有一个最完美的增量序列公式,这里选用全为t/2向下取整。
希尔排序必须保证最后一次划分间隔为1,希尔排序又叫缩小增量排序。
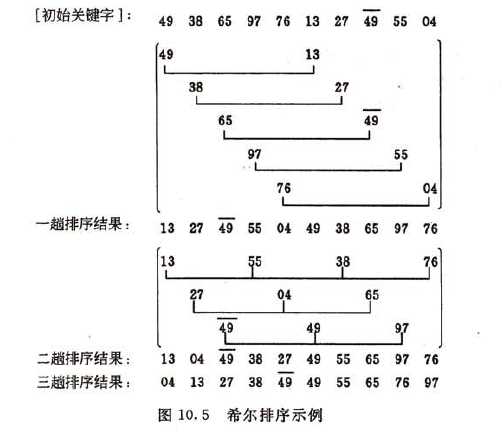
(这里盗用数据结构书上的图了~,可以说是很形象了,不过图中选取的增量序列是 t - 2)
void shellSort(int*data, unsigned int len) { for (int div = len / 2; div >= 1; div = div / 2) { for (int i = 0; i < div; ++i) { for (int j = i + div; j < len; j += div) { int k, temp = data[j]; for (k = j - div; k >= 0 && temp < data[k]; k -= div) { data[k + div] = data[k]; } data[k + div] = temp; /*for (k = j; k >= div && temp < data[k - div]; k -= div) { data[k] = data[k - div]; } data[k] = temp;*/ } } } }
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序利用了完全二叉树特性,是一种十分高效的稳定排序。
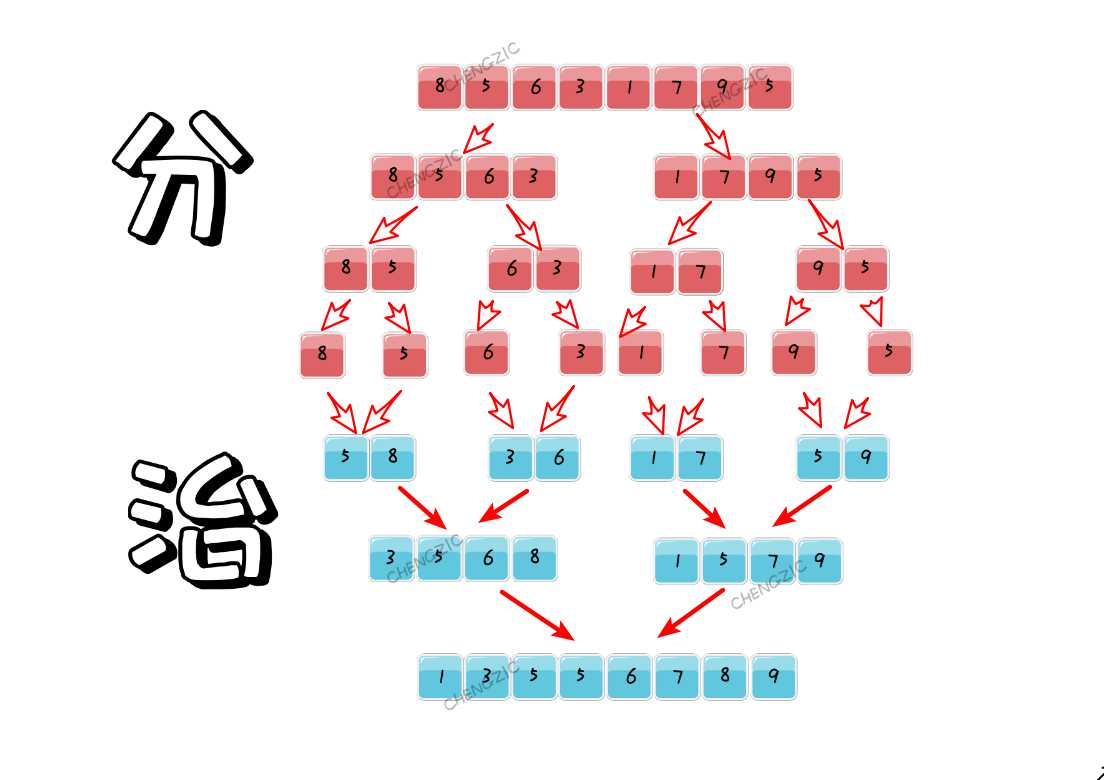
void meger(int *a, int left, int mid, int right) { int *b = new int[right - left + 1]; int t = 0, i = left, j = mid + 1; while (i <= mid && j <= right) { b[t++] = a[i] < a[j] ? a[i++] : a[j++]; } while (i <= mid) b[t++] = a[i++]; while (j <= right) b[t++] = a[j++]; i = left; t = 0; while (i <= right) a[i++] = b[t++]; delete[]b; } void megerSort(int *a, int left, int right) { if (left == right) return; int mid = (right + left) >> 1; megerSort(a, left, mid); megerSort(a, mid + 1, right); meger(a, left, mid, right); }
快速排序的思想很简单,就是先确定一个基准 SIGN,左右开工,从两边遍历数组将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
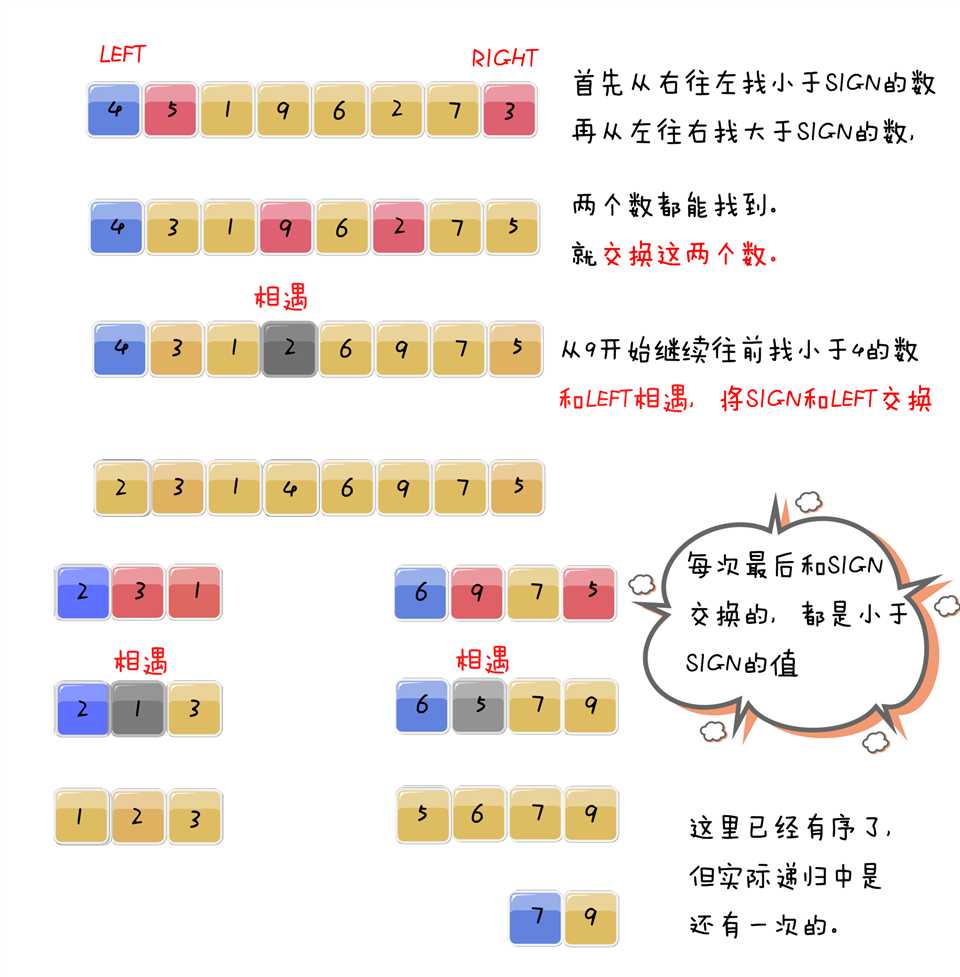
快速排序选取第一个元素作为基准。这样在数组已经有序的情况下,算法将会降级为O(n^2)。一种比较常见的优化方法是随机化算法,即随机选取一个元素作为基准。
冯·诺依曼·赵四说过:“快速排序是看脸的,人丑排得慢。” 看来我是排不好了。
//low:first index;high:last index void quickSortTest(int *a,int low,int high) { if (low >= high)return; //这里i要等于low,是为了j从hign一直到low都没找到比Sign小的值,就不需要进行交换 int i = low, j = high; int sign = a[low]; while (i < j) { //因为基准值是a[0],所以这里先j--,确保最后换的时候,a[j]是小于等于a[0]的。如果基准值是a[length-1],就是i++了。 while (a[j] >= sign && i < j)j--; while (a[i] <= sign && i < j)i++; swap(a[i], a[j]); } swap(a[low], a[i]); quickSortTest(a, low, i - 1); quickSortTest(a, i + 1, high); }
void partition(int *a, int left, int right) { if (left >= right) return; //获取left到right中的随机值 int sign = rand() % (right - left) + left; swap(a[left], a[sign]); int i = left, j = right; while (i < j) { while (a[j] >= a[left] && i < j)j--; while (a[i] <= a[left] && i < j)i++; swap(a[i], a[j]); } swap(a[left], a[i]); partition(a, left, i - 1); partition(a, i + 1, right); } void RandomQuickSort(int *a,int length) { partition(a, 0, length - 1); }
刚刚看到基数排序原理的时候,老夫脑子里只有一句话:“卧槽??”,很巧妙,而且很简单的思想。不难推出,基数排序适合于处理数据范围小的数据。

基数排序属于很好懂,实现起来,很多小地方,比较繁琐。
重要的是思想,为了缩短代码量,这里借助STL vector 实现了LSD(我怎么这么短系列):
void radixSort(int *a,int length) { //开19个,是为了处理负数,-9 --》9 vector<vector<int>>radix(19); int max = a[0], count = 1, div = 1; //求最大值 for (int i = 1; i < length; i++) max = max > a[i] ? max : a[i]; //求最大位数 while (max /=10 ) count++; while(count--) { for (int i = 0; i < length; i++) { int index = a[i] < 0 ? -a[i] / div % 10 : a[i] / div % 10 + 9; radix[index].push_back(a[i]); } for (int i = 0, j = 0; i < length; j++ ) { int k = 0; while (k < radix[j].size()) a[i++] = radix[j][k++]; radix[j].clear(); } div *= 10; } }
这个是根据百科里的算法改的(百科里的代码竟然没考虑负数的???)
因为把数据装桶的时候,是逆序装的,这里index直接用 a[j] / div % 10 + 9; 就行了
int MaxBit(int a[], int length) { int max = a[0], count = 1, div = 1; for (int i = 1; i < length; i++) max = max > a[i] ? max : a[i]; while (max /= 10) count++; return count; } void radixsort1(int a[], int length) //基数排序 { int i,j,k,bit = MaxBit(a, length); int *tmp = new int[length]; int *count = new int[19]; //计数器 int div = 1; for (i = 1; i <= bit; i++){ memset(count, 0, sizeof(int) * 19); for (j = 0; j < length; j++) { int index = a[j] / div % 10 + 9; count[index]++; } for (j = 1; j < 19; j++) count[j] += count[j - 1]; //后面碰到的要往后放,tmp数组是倒过来的往里存的,这里必须逆序 for (j = length - 1; j >= 0; j--) { int index = a[j] / div % 10 + 9; tmp[count[index]-- - 1] = a[j]; } for (j = 0; j < length; j++) a[j] = tmp[j]; div *= 10; } delete[]tmp; delete[]count; }
8.计数排序
假定20个随机整数的值如下:
9,3,5,4,9,1,2,7,8,1,3,6,5,3,4,0,10,9 ,7,9
遍历随机数列,每一个整数按照其值对号入座,对应数组下标的元素进行加1操作。
遍历完毕时,数组的状态如下:

直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次:
0,1,1,2,3,3,3,4,4,5,5,6,7,7,8,9,9,9,9,10
朴素版:

void countSort(int *a, int length) { int min = getMin(a, length); int max = getMax(a, length); int *count = new int[max - min + 1]; memset(count, 0, sizeof(int)*(max - min + 1)); for (int i = 0; i < length; i++) { count[a[i] - min]++; } for (int i = 0, j = 0; j < max - min + 1; j++) { if (count[j] != 0) { while (count[j]--) a[i++] = j + min; } } }
正版:
void countSort(int* a,int length) { int max = getMax(a,length); int min = getMin(a, length); int offset = max - min; int* countArray = new int[offset + 1]; memset(countArray, 0, sizeof(int)*(offset + 1)); for (int i = 0; i < length; i++) { countArray[a[i] - min]++; } for (int i = 1; i < offset + 1; i++) { countArray[i] += countArray[i-1]; } int* sortedArray = new int[length]; for (int i = length - 1; i >= 0; i--) { //把a[i]放在该放的位置上 sortedArray[countArray[a[i] - min] - 1] = a[i]; countArray[a[i] - min]--; } for (int i = 0; i < length; i++) a[i] = sortedArray[i]; }
1.当数列最大最小值差距过大时,并不适用计数排序。
比如给定20个随机整数,范围在0到1亿之间,这时候如果使用计数排序,需要创建长度1亿的数组。不但严重浪费空间,而且时间复杂度也随之升高。
2.当数列元素不是整数,并不适用计数排序。
如果数列中的元素都是小数,比如25.213,或是0.00000001这样子,则无法创建对应的统计数组。这样显然无法进行计数排序。
9.桶排序
上面说了,当数据范围较大、元素不是整数是不适合或不能使用计数排序,桶排序是计数排序的升级版,不属于比较排序,也不受O(n*logn)下限的影响。
更快的排序,总是以空间为代价的。
第一步:
首先确定有多少个桶,这里选取length个桶,每个桶的区间跨度为(max - min)/(length - 1)(具体建立多少个桶,如何确定桶的区间范围,有很多不同的方式。)
第二步:
遍历原始数列,把元素对号入座放入各个桶中:
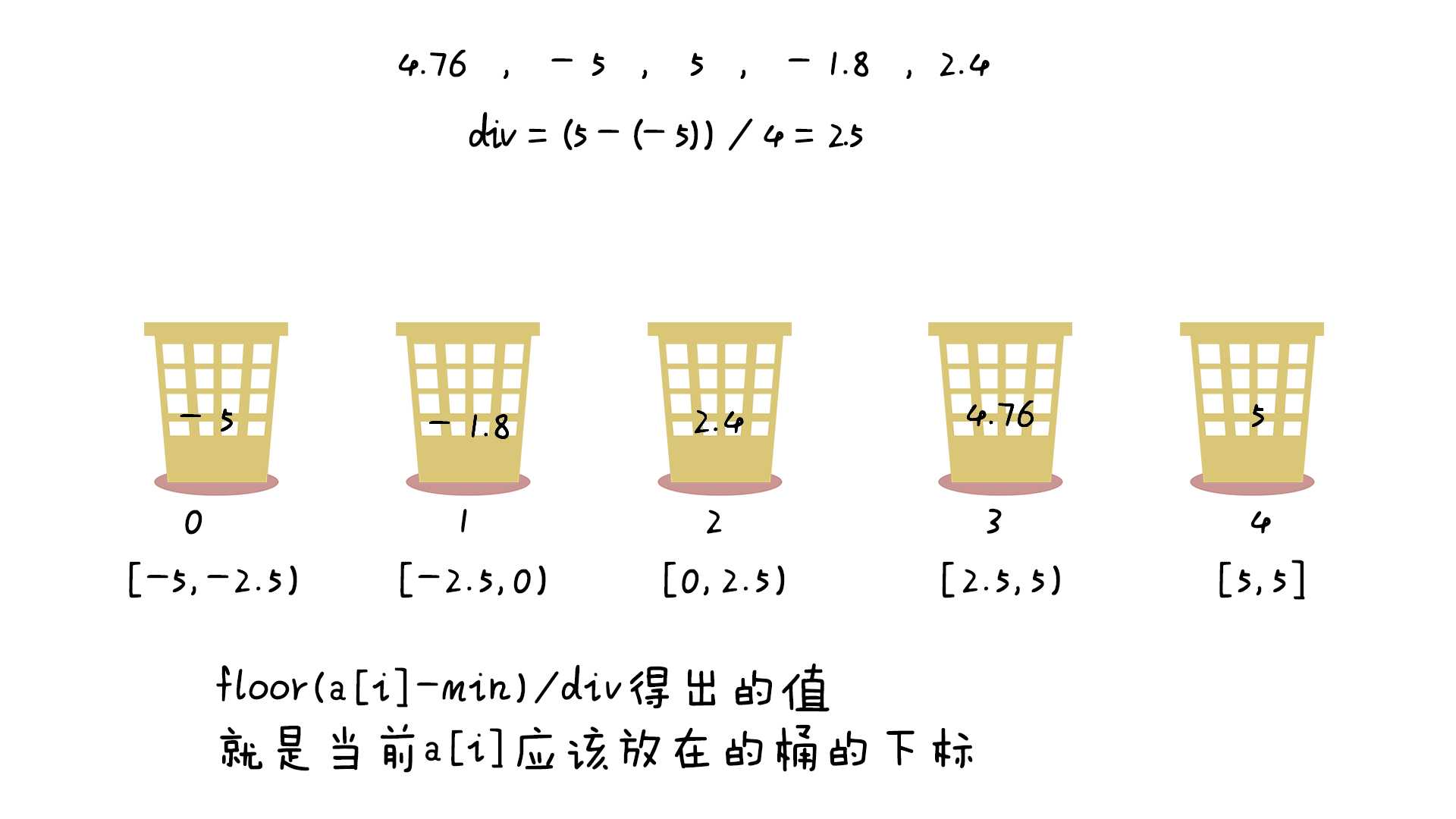
第三步:
每个桶内部的元素分别排序,借助其他简单排序方法。
void bucketSort(int *a, int length) { int min = getMin(a, length); int max = getMax(a, length); double div = (max - min) / (double)(length - 1); vector<vector<int>>bucket(length); for (int i = 0; i < length; i++) { bucket[floor((a[i] - min) / div)].push_back(a[i]); } for (int i = 0; i < length; i++) { //对每个桶 进行插入排序 for (int j = 1; j < bucket[i].size(); j++) { int k,sign = bucket[i][j]; for (k = j; k > 0 && sign < bucket[i][k - 1]; k--) { bucket[i][k] = bucket[i][k - 1]; } bucket[i][k] = sign; } } for (int i = 0, k = 0; i < length; i++) { for (int j = 0; j < bucket[i].size(); j++) { a[k++] = bucket[i][j]; } bucket[i].clear(); } }
桶排序克服了计数排序上述的两个问题,但桶排序希望数据是均匀分布的,否则,所有数据全都进了一个桶,就退化成你使用的桶内排序方法了。
十、堆排序
想实现堆排序,必须要先了解二叉堆,堆排序就是,就是循环移除顶部元素到数组末尾,然后 自上而下 Sink重建堆的操作。
堆排序可以分为两步:
1)根据初始数组去构造一个最大堆
从最后一个父节点开始往上,用 Sink 调整最大堆,堆顶数组为最大元素。
2)每次交换第一个和最后一个元素,length--,然后把剩下元素重新调整为最大堆。
这里需要知道几点:
数组下标是从0开始的,对于构建出来的二叉堆,第k个元素的左孩子就是2*k+1,右孩子是2*k+2
最大堆要求,所有子节点不大于堆顶,所以是可以处理存在重复数字的数组的。
void Sink(int *a, int index,int length) {
//如果元素有左孩子 while (index * 2 + 1 < length) { int left = index * 2 + 1; if (left + 1 <= length - 1 && a[left] < a[left + 1]) left++; if (a[index] > a[left])break; swap(a[index], a[left]); index = left; } } void heapSort(int *a,int length) { for (int i = length / 2 - 1; i >= 0; i--) Sink(a, i, length); while(length--) { swap(a[0], a[length]); Sink(a, 0, length); } }
标签:one 交换 aik 序列 增量排序 选择 归并 quic sorted
原文地址:https://www.cnblogs.com/czc1999/p/10266436.html