标签:arm 它的 小项目 性能 私钥 plain 现在 .com 加密和解密
这段时间的博客是作者本科毕业设计的周期性小报告,考虑到公开可浏览,故写成了这种略带密码学科普性的博客,在提交周期性工作汇报的同时分享一些学习密码学时的心得,欢迎大家批评指正。
本系列主要内容为SM2/3/4/9系列算法的简单介绍和python的实现方式,也可能有时会添加一些为其它同学做的小玩意,请相信作者都是字字手码,尽量让对密码学有兴趣的同学们都能看懂。python版本为3.6.6,有编程基础者约一周可上手,推荐小甲鱼系列丛书,但愿对各位同学的学习和工作有所帮助。再次感谢老师同学的多多评论,欢迎批评指正,共同进步!
2012年3月21日,国家密码管理局发布了一种分组密码标准,标准为GM/T 0002-2012《SM4分组密码算法》(原SMS4分组密码算法),作为我国商用密码标准算法使用至今。
根据需要保守秘密的重要性,我国对信息安全划分为多个等级,分别使用不同的保护方式进行保障,商用密码仅能保护与国家秘密无关的,泄露后对国家安全不构成任何威胁的信息。是我国广大人民群众所能接触到的最多的密码。
商用密码算法有很多,比较出名的如:AES、ZUC、RSA等,都是用来保护企业非涉及国家机密的敏感商业信息以及个人隐私信息的,根据密码学对于密码算法的分类,商用密码也分为以下几类:
对称当然是指密钥的对称使用,就如同古典密码,加解密双方要有一个一模一样的东西才能完成加密和解密操作,这有可能是密码本、一个同样的规则,也有可能是一根一样粗的小木棒~在现代密码学上来讲,这个东西就是密钥!
问题来了,现代商用密码的国际标准要被很多人使用,也就是说商用密码算法的运算步骤本身根本没有机密性可言。若要保护好密码内部蕴含的信息,在你信任该密码算法还不足以被攻破的情况下,只能完全依赖密钥的保密。
对称密钥大体上也分为两类:
序列密码:也称流密码(Stream Cipher),顾名思义,它的密钥流会像一条河流一样,不停地输出,然后与待加密的明文对位异或,完成加密操作。加密方使用一个短字节的密钥输入到密码模块中,密码模块就会根据密钥输入不停计算并产生用于加密的密钥流,解密方只要将同样的密钥输入模块中,就可以得到相同的密钥流,异或密文完成解密。其优势也很明显,较好性能的序列密码算法的加密效率极高,非常适合用于通信加密这种实时性较强,短时间加密效率需求较高的场合之中。
分组密码:也称块密码(Block Cipher),该密码将明文分成等长的“组”或者称“块”,密码算法对这其中的每一个明文块进行运算加密,将结果连接在一起后就会得到密文数据。加密方将密钥输入到密码模块中,让密码算法对其中的每个分组进行加密,解密方反向运行密码算法,即可使用相同的密钥恢复得到明文。该密码在明文数据本身含有分块的情形下有着天然优势,仅修改某一分组的内容即可完成密文的修改更新,但也有可能暴露明文分组的特征,这里可以应用一些分组密码的工作模式避免。本章介绍的SM4密码算法讲的就是这种密码。
由于这块不是今天的重点,这里仅介绍一些公钥密码皮毛上的东西,后面再进行补充。
假设这样一种情况,有人用一些数据算出了一个数据,然后将其中一个非结果的数据去掉了,将这些数据给你让你算丢掉的那个数据,你却发现解出这个数据需要其它数据的帮助才能完成,否则将十分困难。当这种现象被放大的时候,就出现了当前的公钥密码算法,其精髓在于制造陷门。
这种密码通常需要根据一些数学难题,难到什么程度?经理论证明目前的计算能力得不出解或者解密代价远大于信息本身价值的难度。这种密码的特征就是加密时用到的密钥和解密时用到的密钥是完全不一样却又有某种关系的。
这种密码还成全了电子签名,由于每个使用公钥密码的账户都具备一组公私钥对,其中私钥是除账户本人以外无法获取到的,依靠这一特性,私钥就可以进行计算生成一个数据,也就是签名,需要时由他人用公钥进行验证,证明所签名的信息一定是来自该账户。
如同现行国际标准的密码算法,SM4同样分为两部分:加密轮函数和密钥扩展函数。
同样需要用到一些常见的模块:S盒混乱层,扩散置换层。
密钥标准长度和分组固定长度都为128bit,所以每组的输出也为128bit
SM4是对“字”友好的算法,一个字节长度为8bit,一个字长度为4个字节,也就是32bit。SM4算法中,32bit的操作非常多,一方面是为了提高运行效率,另一方面也是为了一次性处理整数个字时的方便。
SM4在运行前要配置一些参数:
主密钥(128bit),括号中每个变量表示一个字,下同
MK=(MK0,MK1,MK2,MK3)系统参数(128bit)
FK=(FK0,FK1,FK2,FK3)固定参数(128bit)
CK=(CK0,CK1,...,CK31)准备好了吗?下面才是干货!往下看↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
这个部分跟咱揉面团一样,要把黄油、鸡蛋等充分渗入面糊中,成为一个整体,看不出他们的本来面貌!话不多说,直接上一个SM4轮函数的示意图:
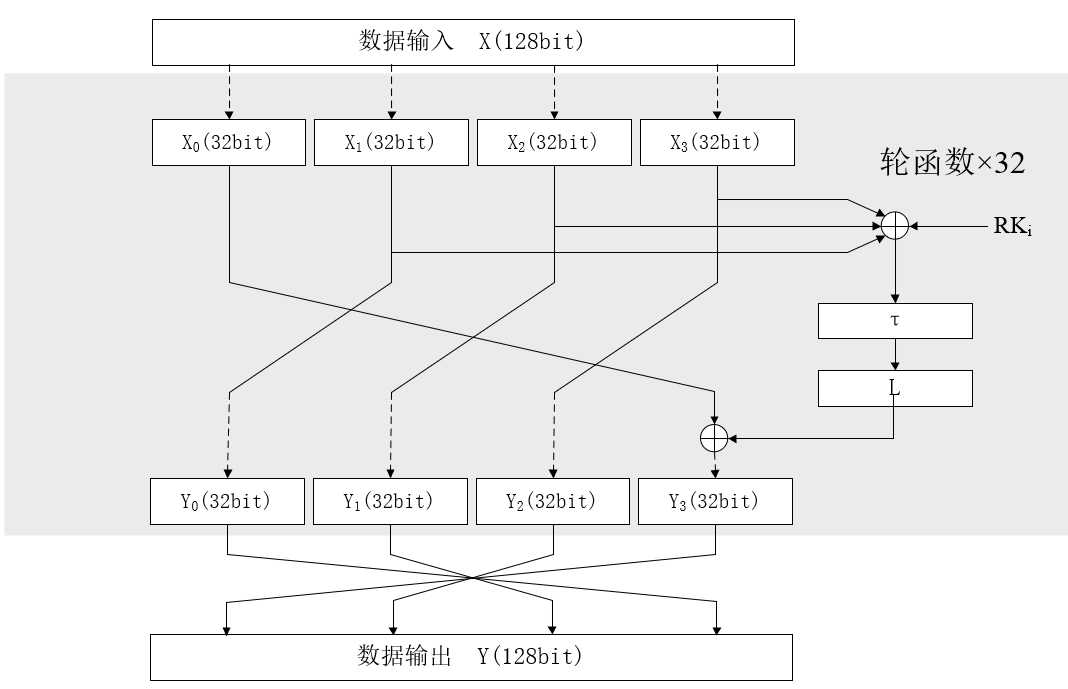
解释一下,SM4的轮函数将输入部分看做了4个32bit长度的数据,每轮的后3个部分都向左移动32bit的数据长度,这三组数据异或后进入非线性部分τ和线性部分L,运算后的结果与第一组数据异或置于最右面。如此循环往复32轮,也就是数据一共左移了8个周期,将其中的混乱因素不断扩散至每个bit位中。最后将4段数据反序置放,如此才能在解密时重复利用现有的结构。
解密时,函数将进行加密时的逆运算,所以,在编程时,S盒应该反用,轮密钥应该从后开始一次向前使用。
下面进行模块解释。
这个部分由4个8bit进8bit输出的S盒组成。S盒是什么?像是曾经使用的密码本,上面每个字都对应着不同的信号。这里使用的S盒是一种256个数到256个数的映射,因为其具有较好的非线性程度等良好的密码学性质,比较适合用作数据混乱的核心工具。用公式表达τ函数为:
B=τ(A)=(Sbox(a_0),Sbox(a_1),Sbox(a_2),Sbox(a_3))直观点的图如下:
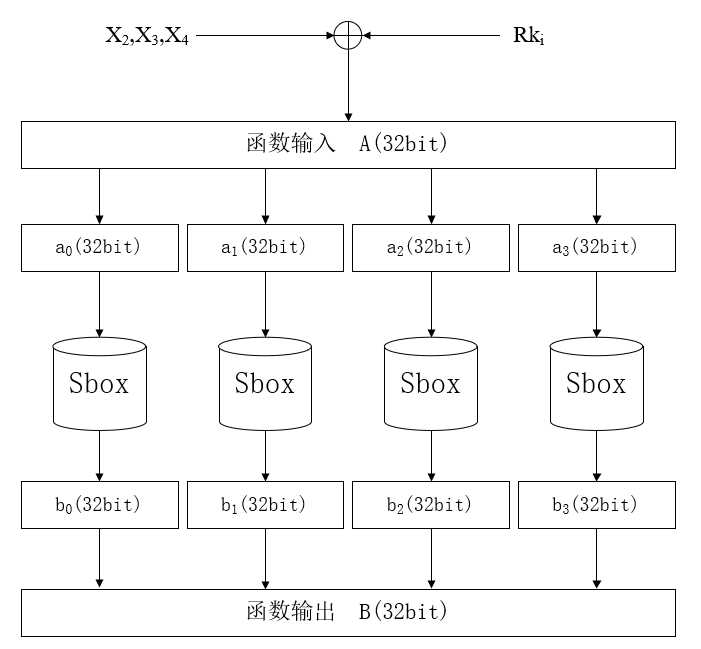
经过4个S盒进行非线性映射后的数据,与原数据没有直观的数学关系,是抵抗线性分析非常有效的工具。
线性置换换成人话就是把比特位互相挪一挪,这样一来,对应字节(8bit)的混乱将会影响到其它字节,提高非线性部分的混乱效果。由于置换属于线性变换,一般没有密码算法会使用完全由线性变换堆砌而成,线性变换对于分析者来说复杂程度很低,很容易找到线性变换的规律,写出公式将密文破解。线性置换部分L函数的定义为:
C=L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)直观解释为将B(τ函数的输出值,32bit)分别左移2,10,18,24比特后,与其自身一同异或,即可将比特位影响到其它位置。【<<<表示向左循环移位】像移位、异或等这些操作都属于线性运算,硬件实现方便,软件实现同样高效,作为密码算法中辅助混乱扩散的重要部分,在算法中大量普遍存在。
加密轮函数的结果输出剩下最后的一次异或操作,公式表示形式为:
X[i+4]=F(X[i],X[i+1],X[i+2],X[i+3])=X[i]⊕T(X[i+1]⊕X[i+2]⊕X[i+3]⊕RK[i]),i=0,1,...,31.其中,T函数包含τ函数和L函数:T=L(τ(X‘))
现在我们知道加密轮函数共需要32轮,如果这些都使用同样的轮密钥,安全系数会大打折扣。SM4对参与轮函数运算的轮密钥RK进行了一番处理,使之变得杂乱不同,有助于提供混乱程度,让密钥对待加密数据产生影响。
SM4在运行前载入的参数将在这一步发挥作用!看图↓↓↓
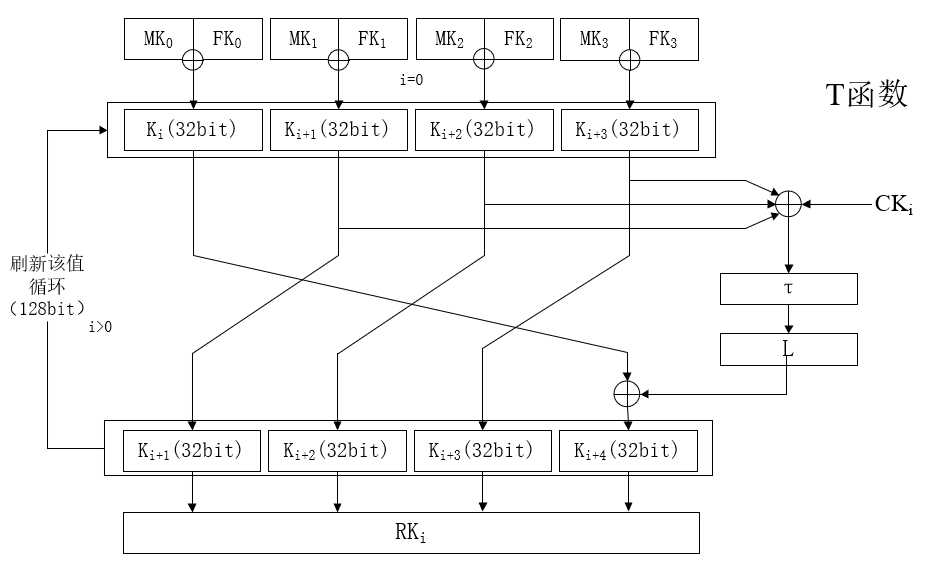
看上去是不是和轮密钥的结构是一样的?这样在硬件实现上避免了单独制作一个轮密钥扩展电路,降低了电路门数,是一种不错的解决方法。这种结构生成的轮密钥是非线性度较高的,系统参数还能确保SM4算法在不同的应用环境中隔离使用,不同的系统中使用不同的系统参数,即使使用相同的密钥也无法加密加密,无法正常通信。
这里面的非线性部分τ同加密轮函数部分的τ函数,但线性置换部分有点改动,表述如下:
L‘(B)=B⊕(B<<<13)⊕(B<<<23)如此,整个密钥扩展函数表述为下式:
RK[i]=K[i+4]=K[i]⊕T‘(K[i]⊕K[i+2]⊕K[i+3]⊕CK[i])讲到这里,SM4的大概状况就已经说完啦,下面我们考虑怎么实现它!
我们首先用一个笨笨的办法尝试实现它,只加密一组数据,学过一门编程语言的人都是很容易看懂的!
就像C语言一样,我们写几个子函数,让我们的变量去做一些固定的操作。这个是无需加载任何python库的一个基础方法,所以代码上看起来还是略显复杂,但更能直观表达我们的算法步骤。
理清这个思路:由于咱们做的是单线程的、比较笨的初级程序,程序具有较强的顺序层次,所以我们要按顺序来,先载入基本参数:主密钥(MK),系统参数(FK)和固定参数(CK)。CK已经在程序中展示出来了;其次,要先产生轮密钥,也就是进行密钥扩展,最后进行加密轮函数运算。因为固定参数要应用于轮密钥生成中,轮密钥作为轮函数的输入要参与运算,所以程序的运算顺序是确定的,不能更改的。明白这些的话,就往下看,直接给出我写的主函数↓↓↓
################################### MAIN FUNCTION ################################
##初始化,载入主密钥、系统参数和固定参数
CK = [ ‘\x00\x07\x0e\x15‘ , ‘\x1c\x23\x2a\x31‘ , ‘\x38\x3f\x46\x4d‘ , ‘\x54\x5b\x62\x69‘ , ‘\x70\x77\x7e\x85‘ , ‘\x8c\x93\x9a\xa1‘ , ‘\xa8\xaf\xb6\xbd‘ , ‘\xc4\xcb\xd2\xd9‘ ,
‘\xe0\xe7\xee\xf5‘ , ‘\xfc\x03\x0a\x11‘ , ‘\x18\x1f\x26\x2d‘ , ‘\x34\x3b\x42\x49‘ , ‘\x50\x57\x5e\x65‘ , ‘\x6c\x73\x7a\x81‘ , ‘\x88\x8f\x96\x9d‘ , ‘\xa4\xab\xb2\xb9‘ ,
‘\xc0\xc7\xce\xd5‘ , ‘\xdc\xe3\xea\xf1‘ , ‘\xf8\xff\x06\x0d‘ , ‘\x14\x1b\x22\x29‘ , ‘\x30\x37\x3e\x45‘ , ‘\x4c\x53\x5a\x61‘ , ‘\x68\x6f\x76\x7d‘ , ‘\x84\x8b\x92\x99‘ ,
‘\xa0\xa7\xae\xb5‘ , ‘\xbc\xc3\xca\xd1‘ , ‘\xd8\xdf\xe6\xed‘ , ‘\xf4\xfb\x02\x09‘ , ‘\x10\x17\x1e\x25‘ , ‘\x2c\x33\x3a\x41‘ , ‘\x48\x4f\x56\x5d‘ , ‘\x64\x6b\x72\x79‘ ]
MK = ""
while len(MK) < 16 :
MK = input( "请输入本次服务的SM4主密钥:" )
##这里一定要对 MK 的长度进行检测,以确保不会出现错误!
if len(MK) >= 16 :
MK = MK[0:16]
else :
print( "密钥长度不足,请至少输入128bit数据,我们将截取您的前128bit数据作为主密钥" )
print ( "MK =" , MK )
##↓这是系统参数,由于每个系统在安装时都会确定该值,通常不与用户互动,这里我们直接写一个128bit的常量到代码中即可
FK = "ZhaoWenhao155104"
FK = FK[0:16]
##开始进行密钥扩展
print( "轮密钥生成中……" )
RK = []
Attr = strxor( MK , FK , 16 )
for i in range (0,32):
Attr = functionTK( Attr , CK , i )
RK.append( Attr[12:16] )
print( "RK [" , i+1 , "]" , str2hex(RK[i]) )
##加密轮函数启动
plain = ""
while len(plain) < 16 :
plain = input( "正在准备启动SM4算法,请输入明文:" )
if len(plain) >= 16 :
plain = plain[0:16]
else :
print( "明文长度不足,请至少输入128bit数据,我们将截取您的前128bit数据作为明文" )
print ( " plain =" , str2hex(plain) )
Attr = plain
for i in range (0,32) :
Attr = functionT( Attr , RK , 1 , i )
cipher = Attr[12:16] + Attr[8:12] + Attr[4:8] + Attr[0:4]
print( "cipher =" , str2hex(cipher) )有些明显是定义的函数不知道是什么?不着急,慢慢向下看,咱会一点一点给出来的。作者本人是很自信大部分人能看懂这个逻辑的。程序中加入了输入的检测,防止因为输入长度不够导致程序运行时出现bug,去掉那个CK长长的定义和检错部分,剩下的代码就不多了,是不是很像C语言的伪代码?大概看一下,不难猜到functionT和functionTK分别指加密轮函数的一轮和密钥扩展函数的一轮。为了体现轮数,咱把循环写在主函数里了,其实主函数还可以更简洁不是吗?后面我们再对这个粗代码进行整理。下面给出他们的定义:
##字符串的S盒查表
## Act=1时表示执行加密状态,S盒要将对应位置的字符串找到,替换原字符
## Act等于其他值时为解密状态,要将特定字符的位置找到,将号码转换为字符替换原字符(其实是-1,写代码时else了事)
def SearchSbox( reg , Act ):
out = ""
Sbox = [‘\xd6‘ , ‘\x90‘ , ‘\xe9‘ , ‘\xfe‘ , ‘\xcc‘ , ‘\xe1‘ , ‘\x3d‘ , ‘\xb7‘ , ‘\x16‘ , ‘\xb6‘ , ‘\x14‘ , ‘\xc2‘ , ‘\x28‘ , ‘\xfb‘ , ‘\x2c‘ , ‘\x05‘,
‘\x2b‘ , ‘\x67‘ , ‘\x9a‘ , ‘\x76‘ , ‘\x2a‘ , ‘\xbe‘ , ‘\x04‘ , ‘\xc3‘ , ‘\xaa‘ , ‘\x44‘ , ‘\x13‘ , ‘\x26‘ , ‘\x49‘ , ‘\x86‘ , ‘\x06‘ , ‘\x99‘,
‘\x9c‘ , ‘\x42‘ , ‘\x50‘ , ‘\xf4‘ , ‘\x91‘ , ‘\xef‘ , ‘\x98‘ , ‘\x7a‘ , ‘\x33‘ , ‘\x54‘ , ‘\x0b‘ , ‘\x43‘ , ‘\xed‘ , ‘\xcf‘ , ‘\xac‘ , ‘\x62‘,
‘\xe4‘ , ‘\xb3‘ , ‘\x1c‘ , ‘\xa9‘ , ‘\xc9‘ , ‘\x08‘ , ‘\xe8‘ , ‘\x95‘ , ‘\x80‘ , ‘\xdf‘ , ‘\x94‘ , ‘\xfa‘ , ‘\x75‘ , ‘\x8f‘ , ‘\x3f‘ , ‘\xa6‘,
‘\x47‘ , ‘\x07‘ , ‘\xa7‘ , ‘\xfc‘ , ‘\xf3‘ , ‘\x73‘ , ‘\x17‘ , ‘\xba‘ , ‘\x83‘ , ‘\x59‘ , ‘\x3c‘ , ‘\x19‘ , ‘\xe6‘ , ‘\x85‘ , ‘\x4f‘ , ‘\xa8‘,
‘\x68‘ , ‘\x6b‘ , ‘\x81‘ , ‘\xb2‘ , ‘\x71‘ , ‘\x64‘ , ‘\xda‘ , ‘\x8b‘ , ‘\xf8‘ , ‘\xeb‘ , ‘\x0f‘ , ‘\x4b‘ , ‘\x70‘ , ‘\x56‘ , ‘\x9d‘ , ‘\x35‘,
‘\x1e‘ , ‘\x24‘ , ‘\x0e‘ , ‘\x5e‘ , ‘\x63‘ , ‘\x58‘ , ‘\xd1‘ , ‘\xa2‘ , ‘\x25‘ , ‘\x22‘ , ‘\x7c‘ , ‘\x3b‘ , ‘\x01‘ , ‘\x21‘ , ‘\x78‘ , ‘\x87‘,
‘\xd4‘ , ‘\x00‘ , ‘\x46‘ , ‘\x57‘ , ‘\x9f‘ , ‘\xd3‘ , ‘\x27‘ , ‘\x52‘ , ‘\x4c‘ , ‘\x36‘ , ‘\x02‘ , ‘\xe7‘ , ‘\xa0‘ , ‘\xc4‘ , ‘\xc8‘ , ‘\x9e‘,
‘\xea‘ , ‘\xbf‘ , ‘\x8a‘ , ‘\xd2‘ , ‘\x40‘ , ‘\xc7‘ , ‘\x38‘ , ‘\xb5‘ , ‘\xa3‘ , ‘\xf7‘ , ‘\xf2‘ , ‘\xce‘ , ‘\xf9‘ , ‘\x61‘ , ‘\x15‘ , ‘\xa1‘,
‘\xe0‘ , ‘\xae‘ , ‘\x5d‘ , ‘\xa4‘ , ‘\x9b‘ , ‘\x34‘ , ‘\x1a‘ , ‘\x55‘ , ‘\xad‘ , ‘\x93‘ , ‘\x32‘ , ‘\x30‘ , ‘\xf5‘ , ‘\x8c‘ , ‘\xb1‘ , ‘\xe3‘,
‘\x1d‘ , ‘\xf6‘ , ‘\xe2‘ , ‘\x2e‘ , ‘\x82‘ , ‘\x66‘ , ‘\xca‘ , ‘\x60‘ , ‘\xc0‘ , ‘\x29‘ , ‘\x23‘ , ‘\xab‘ , ‘\x0d‘ , ‘\x53‘ , ‘\x4e‘ , ‘\x6f‘,
‘\xd5‘ , ‘\xdb‘ , ‘\x37‘ , ‘\x45‘ , ‘\xde‘ , ‘\xfd‘ , ‘\x8e‘ , ‘\x2f‘ , ‘\x03‘ , ‘\xff‘ , ‘\x6a‘ , ‘\x72‘ , ‘\x6d‘ , ‘\x6c‘ , ‘\x5b‘ , ‘\x51‘,
‘\x8d‘ , ‘\x1b‘ , ‘\xaf‘ , ‘\x92‘ , ‘\xbb‘ , ‘\xdd‘ , ‘\xbc‘ , ‘\x7f‘ , ‘\x11‘ , ‘\xd9‘ , ‘\x5c‘ , ‘\x41‘ , ‘\x1f‘ , ‘\x10‘ , ‘\x5a‘ , ‘\xd8‘,
‘\x0a‘ , ‘\xc1‘ , ‘\x31‘ , ‘\x88‘ , ‘\xa5‘ , ‘\xcd‘ , ‘\x7b‘ , ‘\xbd‘ , ‘\x2d‘ , ‘\x74‘ , ‘\xd0‘ , ‘\x12‘ , ‘\xb8‘ , ‘\xe5‘ , ‘\xb4‘ , ‘\xb0‘,
‘\x89‘ , ‘\x69‘ , ‘\x97‘ , ‘\x4a‘ , ‘\x0c‘ , ‘\x96‘ , ‘\x77‘ , ‘\x7e‘ , ‘\x65‘ , ‘\xb9‘ , ‘\xf1‘ , ‘\x09‘ , ‘\xc5‘ , ‘\x6e‘ , ‘\xc6‘ , ‘\x84‘,
‘\x18‘ , ‘\xf0‘ , ‘\x7d‘ , ‘\xec‘ , ‘\x3a‘ , ‘\xdc‘ , ‘\x4d‘ , ‘\x20‘ , ‘\x79‘ , ‘\xee‘ , ‘\x5f‘ , ‘\x3e‘ , ‘\xd7‘ , ‘\xcb‘ , ‘\x39‘ , ‘\x48‘]
if Act == 1 :
for i in range (0,4) :
out = out + Sbox[ord(reg[i])]
else :
for i in range (0,4) :
out = out + chr(Sbox.index(reg[i]))
return reg
## 轮函数单轮函数,Act同上,其实没必要传递这个i参数,为了严谨表意还是加上了
def functionT( Attr , RK , Act , i ) :
if Act == 1 :
reg = strxor( strxor( Attr[4:8] , Attr[8:12] , 4 ) , strxor( Attr[12:16] , RK[i] , 4 ) , 4 )
reg = SearchSbox ( reg , 1 )
else :
reg = strxor( strxor( Attr[4:8] , Attr[8:12] , 4 ) , strxor( Attr[12:16] , RK[31-i] , 4 ) , 4 )
reg = SearchSbox ( reg , -1 )
reg = strxor( strxor( strxor( reg , strldc(reg,2) , 4 ) , strxor( strldc(reg,10) , strldc(reg,18) , 4 ) , 4 ) , strldc(reg,24) , 4 )
Attr = Attr[4:16] + strxor(Attr[0:4],reg,4)
return Attr
## 密钥扩展单轮函数,Act同上
def functionTK( Attr , CK , i ) :
reg = strxor( strxor( Attr[4:8] , Attr[8:12] , 4 ) , strxor( Attr[12:16] , CK[i] , 4 ) , 4 )
reg = SearchSbox ( reg , 1 )
reg = strxor( strxor( reg , strldc(reg,13) , 4 ) , strldc(reg,23) , 4 )
Attr = Attr[4:16] + strxor(Attr[0:4],reg,4)
return Attr感觉我写得也不很复杂。。。由于两部分的置换层是不一致的,故这里还是将相似的结构写成了两个函数(PS.反正也没几行字……)对照流程图可以看得出来,函数的第一个语句表示4个部分的异或;第二个语句是非线性部分,也就是S盒查找;第三句是置换部分,实质是移位后的异或,最后重新整理状态区,整理成下一轮进行时要输入的形态。
最后就是一些小玩意啦!这里的字符串中比特位的操作也提供给大家!不想去找现有库的各位,这个也可以凑合用用:
## 字符串对应比特位异或,不要在意这个变量名称,因为是写序列密码名称时写的,懒得改……
def strxor( message , key , len ):
out = ""
for i in range ( 0 , len ):
ch = ord(message[i]) ^ ord(key[i])
out = out + chr(ch)
return out
## 字符串转换为每一字节的16进制字符串
def str2hex( string ):
out = ""
for i in range ( 0 , len(string) ):
out = out + " " + hex(ord( string[i] ))
return out
## 字符串的循环左移位,移位数量单位为比特(PS.要不是网上不靠谱我才不会写这些小东西)里面双斜杠不是注释……
def strldc( string , bit ):
byte = bit // 8
bit = bit % 8
out = ""
if bit == 0 :
out = string[byte:] + string[:byte]
else :
reg = string[byte:] + string[:byte+1]
for i in range (0,len(reg)-1):
out = out + chr(((ord(reg[i])*(2**bit))+(ord(reg[i+1])//(2**(8-bit))))%256)
out = out[:len(string)]
return out这样一来,一个单组加密的SM4测试程序就此介绍完了,哪些地方有错欢迎大家批评指正!感谢各位!下面将完整代码,加上解密部分的程序一并展示如下,方便取用↓↓↓:
def strxor( message , key , len ):
out = ""
for i in range ( 0 , len ):
ch = ord(message[i]) ^ ord(key[i])
out = out + chr(ch)
return out
def str2hex( string ):
out = ""
for i in range ( 0 , len(string) ):
out = out + " " + hex(ord( string[i] ))
return out
def strldc( string , bit ):
byte = bit // 8
bit = bit % 8
out = ""
if bit == 0 :
out = string[byte:] + string[:byte]
else :
reg = string[byte:] + string[:byte+1]
for i in range (0,len(reg)-1):
out = out + chr(((ord(reg[i])*(2**bit))+(ord(reg[i+1])//(2**(8-bit))))%256)
out = out[:len(string)]
return out
def SearchSbox( reg , Act ):
out = ""
Sbox = [‘\xd6‘ , ‘\x90‘ , ‘\xe9‘ , ‘\xfe‘ , ‘\xcc‘ , ‘\xe1‘ , ‘\x3d‘ , ‘\xb7‘ , ‘\x16‘ , ‘\xb6‘ , ‘\x14‘ , ‘\xc2‘ , ‘\x28‘ , ‘\xfb‘ , ‘\x2c‘ , ‘\x05‘,
‘\x2b‘ , ‘\x67‘ , ‘\x9a‘ , ‘\x76‘ , ‘\x2a‘ , ‘\xbe‘ , ‘\x04‘ , ‘\xc3‘ , ‘\xaa‘ , ‘\x44‘ , ‘\x13‘ , ‘\x26‘ , ‘\x49‘ , ‘\x86‘ , ‘\x06‘ , ‘\x99‘,
‘\x9c‘ , ‘\x42‘ , ‘\x50‘ , ‘\xf4‘ , ‘\x91‘ , ‘\xef‘ , ‘\x98‘ , ‘\x7a‘ , ‘\x33‘ , ‘\x54‘ , ‘\x0b‘ , ‘\x43‘ , ‘\xed‘ , ‘\xcf‘ , ‘\xac‘ , ‘\x62‘,
‘\xe4‘ , ‘\xb3‘ , ‘\x1c‘ , ‘\xa9‘ , ‘\xc9‘ , ‘\x08‘ , ‘\xe8‘ , ‘\x95‘ , ‘\x80‘ , ‘\xdf‘ , ‘\x94‘ , ‘\xfa‘ , ‘\x75‘ , ‘\x8f‘ , ‘\x3f‘ , ‘\xa6‘,
‘\x47‘ , ‘\x07‘ , ‘\xa7‘ , ‘\xfc‘ , ‘\xf3‘ , ‘\x73‘ , ‘\x17‘ , ‘\xba‘ , ‘\x83‘ , ‘\x59‘ , ‘\x3c‘ , ‘\x19‘ , ‘\xe6‘ , ‘\x85‘ , ‘\x4f‘ , ‘\xa8‘,
‘\x68‘ , ‘\x6b‘ , ‘\x81‘ , ‘\xb2‘ , ‘\x71‘ , ‘\x64‘ , ‘\xda‘ , ‘\x8b‘ , ‘\xf8‘ , ‘\xeb‘ , ‘\x0f‘ , ‘\x4b‘ , ‘\x70‘ , ‘\x56‘ , ‘\x9d‘ , ‘\x35‘,
‘\x1e‘ , ‘\x24‘ , ‘\x0e‘ , ‘\x5e‘ , ‘\x63‘ , ‘\x58‘ , ‘\xd1‘ , ‘\xa2‘ , ‘\x25‘ , ‘\x22‘ , ‘\x7c‘ , ‘\x3b‘ , ‘\x01‘ , ‘\x21‘ , ‘\x78‘ , ‘\x87‘,
‘\xd4‘ , ‘\x00‘ , ‘\x46‘ , ‘\x57‘ , ‘\x9f‘ , ‘\xd3‘ , ‘\x27‘ , ‘\x52‘ , ‘\x4c‘ , ‘\x36‘ , ‘\x02‘ , ‘\xe7‘ , ‘\xa0‘ , ‘\xc4‘ , ‘\xc8‘ , ‘\x9e‘,
‘\xea‘ , ‘\xbf‘ , ‘\x8a‘ , ‘\xd2‘ , ‘\x40‘ , ‘\xc7‘ , ‘\x38‘ , ‘\xb5‘ , ‘\xa3‘ , ‘\xf7‘ , ‘\xf2‘ , ‘\xce‘ , ‘\xf9‘ , ‘\x61‘ , ‘\x15‘ , ‘\xa1‘,
‘\xe0‘ , ‘\xae‘ , ‘\x5d‘ , ‘\xa4‘ , ‘\x9b‘ , ‘\x34‘ , ‘\x1a‘ , ‘\x55‘ , ‘\xad‘ , ‘\x93‘ , ‘\x32‘ , ‘\x30‘ , ‘\xf5‘ , ‘\x8c‘ , ‘\xb1‘ , ‘\xe3‘,
‘\x1d‘ , ‘\xf6‘ , ‘\xe2‘ , ‘\x2e‘ , ‘\x82‘ , ‘\x66‘ , ‘\xca‘ , ‘\x60‘ , ‘\xc0‘ , ‘\x29‘ , ‘\x23‘ , ‘\xab‘ , ‘\x0d‘ , ‘\x53‘ , ‘\x4e‘ , ‘\x6f‘,
‘\xd5‘ , ‘\xdb‘ , ‘\x37‘ , ‘\x45‘ , ‘\xde‘ , ‘\xfd‘ , ‘\x8e‘ , ‘\x2f‘ , ‘\x03‘ , ‘\xff‘ , ‘\x6a‘ , ‘\x72‘ , ‘\x6d‘ , ‘\x6c‘ , ‘\x5b‘ , ‘\x51‘,
‘\x8d‘ , ‘\x1b‘ , ‘\xaf‘ , ‘\x92‘ , ‘\xbb‘ , ‘\xdd‘ , ‘\xbc‘ , ‘\x7f‘ , ‘\x11‘ , ‘\xd9‘ , ‘\x5c‘ , ‘\x41‘ , ‘\x1f‘ , ‘\x10‘ , ‘\x5a‘ , ‘\xd8‘,
‘\x0a‘ , ‘\xc1‘ , ‘\x31‘ , ‘\x88‘ , ‘\xa5‘ , ‘\xcd‘ , ‘\x7b‘ , ‘\xbd‘ , ‘\x2d‘ , ‘\x74‘ , ‘\xd0‘ , ‘\x12‘ , ‘\xb8‘ , ‘\xe5‘ , ‘\xb4‘ , ‘\xb0‘,
‘\x89‘ , ‘\x69‘ , ‘\x97‘ , ‘\x4a‘ , ‘\x0c‘ , ‘\x96‘ , ‘\x77‘ , ‘\x7e‘ , ‘\x65‘ , ‘\xb9‘ , ‘\xf1‘ , ‘\x09‘ , ‘\xc5‘ , ‘\x6e‘ , ‘\xc6‘ , ‘\x84‘,
‘\x18‘ , ‘\xf0‘ , ‘\x7d‘ , ‘\xec‘ , ‘\x3a‘ , ‘\xdc‘ , ‘\x4d‘ , ‘\x20‘ , ‘\x79‘ , ‘\xee‘ , ‘\x5f‘ , ‘\x3e‘ , ‘\xd7‘ , ‘\xcb‘ , ‘\x39‘ , ‘\x48‘]
if Act == 1 :
for i in range (0,4) :
out = out + Sbox[ord(reg[i])]
else :
for i in range (0,4) :
out = out + chr(Sbox.index(reg[i]))
return reg
def functionT( Attr , RK , Act , i ) :
if Act == 1 :
reg = strxor( strxor( Attr[4:8] , Attr[8:12] , 4 ) , strxor( Attr[12:16] , RK[i] , 4 ) , 4 )
reg = SearchSbox ( reg , 1 )
else :
reg = strxor( strxor( Attr[4:8] , Attr[8:12] , 4 ) , strxor( Attr[12:16] , RK[31-i] , 4 ) , 4 )
reg = SearchSbox ( reg , -1 )
reg = strxor( strxor( strxor( reg , strldc(reg,2) , 4 ) , strxor( strldc(reg,10) , strldc(reg,18) , 4 ) , 4 ) , strldc(reg,24) , 4 )
Attr = Attr[4:16] + strxor(Attr[0:4],reg,4)
return Attr
def functionTK( Attr , CK , i ) :
reg = strxor( strxor( Attr[4:8] , Attr[8:12] , 4 ) , strxor( Attr[12:16] , CK[i] , 4 ) , 4 )
reg = SearchSbox ( reg , 1 )
reg = strxor( strxor( reg , strldc(reg,13) , 4 ) , strldc(reg,23) , 4 )
Attr = Attr[4:16] + strxor(Attr[0:4],reg,4)
return Attr
################################### MAIN FUNCTION ################################
##初始化,载入主密钥、系统参数和固定参数
CK = [ ‘\x00\x07\x0e\x15‘ , ‘\x1c\x23\x2a\x31‘ , ‘\x38\x3f\x46\x4d‘ , ‘\x54\x5b\x62\x69‘ , ‘\x70\x77\x7e\x85‘ , ‘\x8c\x93\x9a\xa1‘ , ‘\xa8\xaf\xb6\xbd‘ , ‘\xc4\xcb\xd2\xd9‘ ,
‘\xe0\xe7\xee\xf5‘ , ‘\xfc\x03\x0a\x11‘ , ‘\x18\x1f\x26\x2d‘ , ‘\x34\x3b\x42\x49‘ , ‘\x50\x57\x5e\x65‘ , ‘\x6c\x73\x7a\x81‘ , ‘\x88\x8f\x96\x9d‘ , ‘\xa4\xab\xb2\xb9‘ ,
‘\xc0\xc7\xce\xd5‘ , ‘\xdc\xe3\xea\xf1‘ , ‘\xf8\xff\x06\x0d‘ , ‘\x14\x1b\x22\x29‘ , ‘\x30\x37\x3e\x45‘ , ‘\x4c\x53\x5a\x61‘ , ‘\x68\x6f\x76\x7d‘ , ‘\x84\x8b\x92\x99‘ ,
‘\xa0\xa7\xae\xb5‘ , ‘\xbc\xc3\xca\xd1‘ , ‘\xd8\xdf\xe6\xed‘ , ‘\xf4\xfb\x02\x09‘ , ‘\x10\x17\x1e\x25‘ , ‘\x2c\x33\x3a\x41‘ , ‘\x48\x4f\x56\x5d‘ , ‘\x64\x6b\x72\x79‘ ]
MK = ""
while len(MK) < 16 :
MK = input( "请输入本次服务的SM4主密钥:" )
##这里一定要对 MK 的长度进行检测,以确保不会出现错误!
if len(MK) >= 16 :
MK = MK[0:16]
else :
print( "密钥长度不足,请至少输入128bit数据,我们将截取您的前128bit数据作为主密钥" )
print ( "MK =" , MK )
##↓这是系统参数,由于每个系统在安装时都会确定该值,通常不与用户互动,这里我们直接写一个128bit的常量到代码中即可
FK = "ZhaoWenhao155104"
FK = FK[0:16]
##开始进行密钥扩展
print( "轮密钥生成中……" )
RK = []
Attr = strxor( MK , FK , 16 )
for i in range (0,32):
Attr = functionTK( Attr , CK , i )
RK.append( Attr[12:16] )
print( "RK [" , i+1 , "]" , str2hex(RK[i]) )
##加密轮函数启动
plain = ""
while len(plain) < 16 :
plain = input( "正在准备启动SM4算法,请输入明文:" )
if len(plain) >= 16 :
plain = plain[0:16]
else :
print( "明文长度不足,请至少输入128bit数据,我们将截取您的前128bit数据作为明文" )
print ( " plain =" , str2hex(plain) )
Attr = plain
for i in range (0,32) :
Attr = functionT( Attr , RK , 1 , i )
cipher = Attr[12:16] + Attr[8:12] + Attr[4:8] + Attr[0:4]
print( "cipher =" , str2hex(cipher) )
##加密轮函数启动
print("测试程序自动验证解密的正确性,正在解密……")
Attr = cipher
for i in range (0,32) :
Attr = functionT( Attr , RK , 0 , i )
plain_2 = Attr[12:16] + Attr[8:12] + Attr[4:8] + Attr[0:4]
print( "decrypt=" , str2hex(plain_2) )效果如下:
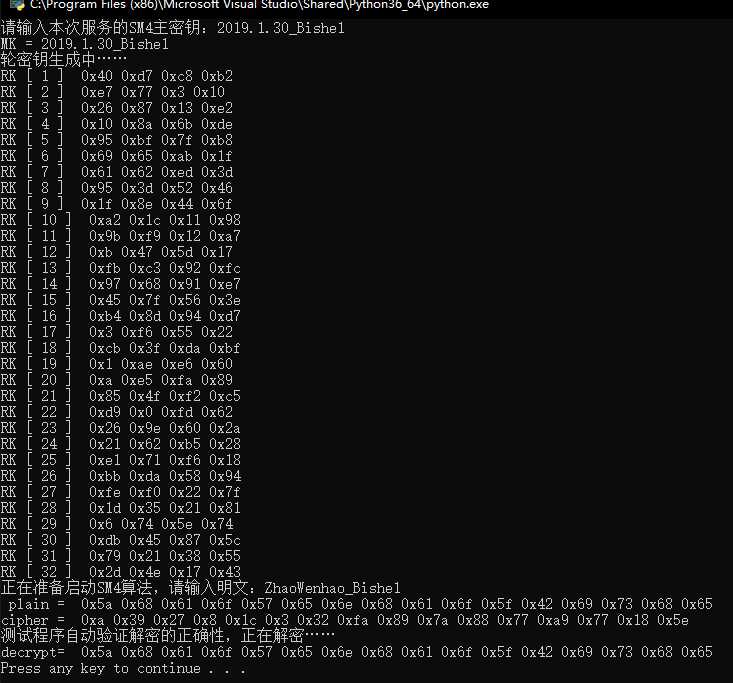
这块的内容单独用一篇来写,做了三天,让本作者歇一小下~准备过年了,祝大家新年快乐!
这边也是一个用python编程才几个月的小白,如果有更强大更巧妙的方式实现请与作者交流,大家共同进步。
由于当代计算机所需处理的密码运算量越来越大,用户对于效率的需求也日益增高,Intel、AMD、ARM等厂商也在寻求一种使密码算法更快实现的方法,这里追加一点小知识,虽然不一定会尝试实现,但也分享在这里。
以下知识总结自论文:
近些年,国内外许多学者尝试将采用SIMD技术的SSE /AVX 指令应用到密码算法的软件实现上。 SIMD的全称是“Single InstructionMultiple Data”,即单指令多数据。该技术可实现同一操作并行处理多组数据。SIMD 技术最大的优点在于它的并行性。2012年,Seiichi和shiho利用SSE指令结合bit-slice技术应用到PRESENT、Piccolo,使二者的实现吞吐量分别达到4.73和4.57cycle/byte。2013年,Neves和Aumasson利用AVX2指令应用到SHA-3候选算法BLAKE上并提高了其实现性能。但是,截至目前,高端处理器(如 Intel Core i7等)上的国产密码SM4优化实现方面的工作尚没有公开发表。
2008年,Intal宣布“Advanced Vector Extensions”(AVX)引入256-bit宽向量指令集,处理数量提升,消除了从内存存取数据时对内存对其的约束,并将操作数提升。2011年,In他了发布AVX2指令集,支持8道32-bit整数异或、移位、置换、查表等。
该指令集为SM4的软件实现有很大好处,无需单独调用字符的异或、移位、置换、查表等函数,即可通过AVX2指令集中的接口指令实现。该指令集不仅使用方便,还在底层指令上进行改进,工作速度更快,并行程度更高。有机会可以尝试使用该指令集编写密码程序,应该会有不错的效果。
论文资源看这里→中国科学院大学学报(2018.3;第35卷第2期)SM4的快速软件实现技术[郞欢,张蕾,吴文玲]
本篇添加了许多一些比较基础的知识,在写这些内容的时候帮助了自己对专业知识的梳理,也让这篇博客更加容易看懂。python目前的学习收获包括程序流掌握、基本数据结构掌握、文件存储掌握、类和对象基本理解、会制作简单的交互界面,接下来的学习中将会在保证密码算法探究的基础上更多学习python编程方面的知识。
由于本科课程中仅学习过的编程语言为C语言,在进入python学习过程中还有一些阻碍需要克服。python对于角标或者叫序号的处理与C语言相比不同,范围角标的左起点包含在范围内而右端点不包含在内,这一点方便从长度上快速计算两端的值,但还需更加适应。python不会将字符串的内容直接以数字形式读出而需要借助BIF的转换,也造成了初期编程的困惑,这些都是比较方便克服的。目前还需解决的重要问题为所需库或者模块的查找,有些时候需要借助现成的方法降低自己的工作量,而不是凡事都要自己写一个小函数,在这一方面我还不够了解,如何更好地查找自己所需的现有工具。在比特位数据处理量较大的密码算法编程中,若每种操作都需要自己实现,这样会造成时间浪费且在非研究重点上过多纠缠。
由于我对SM4流程的某些误读,在写SM4流程的时候也有过多次修改,最终确定没有任何异义。分组密码算法实现中涉及到的数学问题相对较少且每个模块相对简单,但今后涉及到的公钥密码可能会在数学问题上的编程中产生许多问题,这些问题对于我来说需要提前想办法解决。总而言之,SM4算法作为这个工程的开头,算一个比较简单的小项目,今后应加快进度,以准备应对可能遇到的各种难题,感谢老师同学多多协助!
标签:arm 它的 小项目 性能 私钥 plain 现在 .com 加密和解密
原文地址:https://www.cnblogs.com/Qujinkongyuyin/p/10339297.html