树状数组1

标签：树状数组   src   数据   复杂度   出现   问题   查询   png   复杂   

今天花了半个下午的时间可算是把它给搞明白了。。。

什么是树状数组呢？先来看一张图（网上剪的。。。）

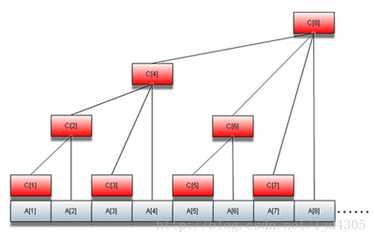
没有看懂没关系，看懂就怪了（滑稽）

树状数组可以做到每一次查询时间复杂度为O（1），并且修改为O（logn），%%%

当看到logn时，难道不应该想到二进制吗？？？

确实，树状数组和二进制有很大的关系，说实话，他和树的关系不大（那他为什么叫树状数组呢？好问题。。。）

简单来说，每一个单元格所储存的数据个数就是他在二进制下从右面往左数直到第一个1出现时，这个1右面的数。（怎样，是不是特别的迷。。。）

举个例子：2（10）存储的个数就是10也就是2，8（1000）就是1000也就是8.

这下就应该明白了吧。

树状数组的建立和修改比较简单，如果只是普通的存储数据就只要在输入时把涉及到的单元格都加上这个数就可以了，先上代码：

1 void add(int x,int k)
2 {
3     while(x<=n)
4     {
5         tree[x]+=k;
6         x+=lowbit(x);
7     }
8 }

你可能会有一些疑问：lowbit是什么呢？

lowbit就是求一个数在二进制下从右往左，直到第一个1出现时这一串数的值，所以我们不断的加上lowbit就可以找到每个存储数据的点了。（不懂的话就再看看图吧。。。）

如果是求区间[x,y]和的话，我们只要求前y个数之和和前x-1个数之和，相减即可，而至于如何求前i个数之和，只要不断减去lowbit即可（还是看图理解吧。。。），附上代码：

 1 int sum(int x)
 2 {
 3     int ans=0;
 4     while(x>0)
 5     {
 6         ans+=tree[x];
 7         x-=lowbit(x);
 8     }
 9     return ans;
10 }

关于区间修改和单点查询，在下一篇博客会详细的讲解（我太懒了。。。）

树状数组1

标签：树状数组   src   数据   复杂度   出现   问题   查询   png   复杂   

原文地址：https://www.cnblogs.com/yufenglin/p/10353757.html