标签:logs hat 第一个 计算 sandy tac 时间 方式 end
在第一篇打分系统漫谈1 - 时间衰减我们聊了两种相对简单的打分算法Hacker News和Reddit Hot Formula,也提出了几个这两种算法可能存在的问题,这一篇我们就其中的两一个问题进一步讨论:
让我们从上一篇我们提到的Reddit Hot Formula来说起,抛开文章质量的惩罚项,只考虑点赞拍砖的低配版打分公式是
\[
score = sign(U-D)* log_{10}{|U-D|} + seconds/4500
\]
Evan从经济学期望效用这个新颖的角度试图对上述公式进行复现,几个基本假设包括:
上述概率p,q可以用已有数据进行估计:
在没有任何和文章相关的信息时,喜欢不喜欢的概率是一样的\(p=\frac{1}{2}\), 当我们获得一篇文章的点赞量和拍砖数时我们可以用点赞率对概率进行更新得到\(p = \frac{U+1}{U+D+2}\)
概率q是一篇t时刻前发布的文章没有被作者读过的概率,换言之就是用户在t时间内没有刷新界面的概率\(q = p(N_\lambda=0)= p(x>t)= exp(-\lambda t)\)
综上我们可以得到对数效用的表达式:
\[ \begin{align} Utility & = p * q -(1-p) * q \\ & = exp(-\lambda t ) *(\frac{U+1}{U+D+2} - \frac{D+1}{U+D+2}) \ &= exp(-\lambda t ) *(\frac{U-D}{U+D+2}) \ log(Utility ) & = log(U-D) - log(U+D+2) - \lambda t \\end{align} \]
和上述Reddit Hot Formula对比我们会发现当U>D的时候,两个表达式是基本一致的,最大的不同是Reddit没有期望效用的第二个对数项\(log(U+D+2)\)。换言之Reddit只考虑点赞量而没有考虑点赞量对应的基数,这个基数可以是点赞+拍砖或者是用户的浏览量。
我们举个例子你就会明白这种打分可能存在的问题,我们拿Stack overflow来举个例子,下图的两个问题获得了差不多的投票57 vs. 53,但是会发现第一个问题比第二个问题多一倍的浏览量4k vs. 2K, 所以从投票率来看反而是第二个问题的投票率更高。
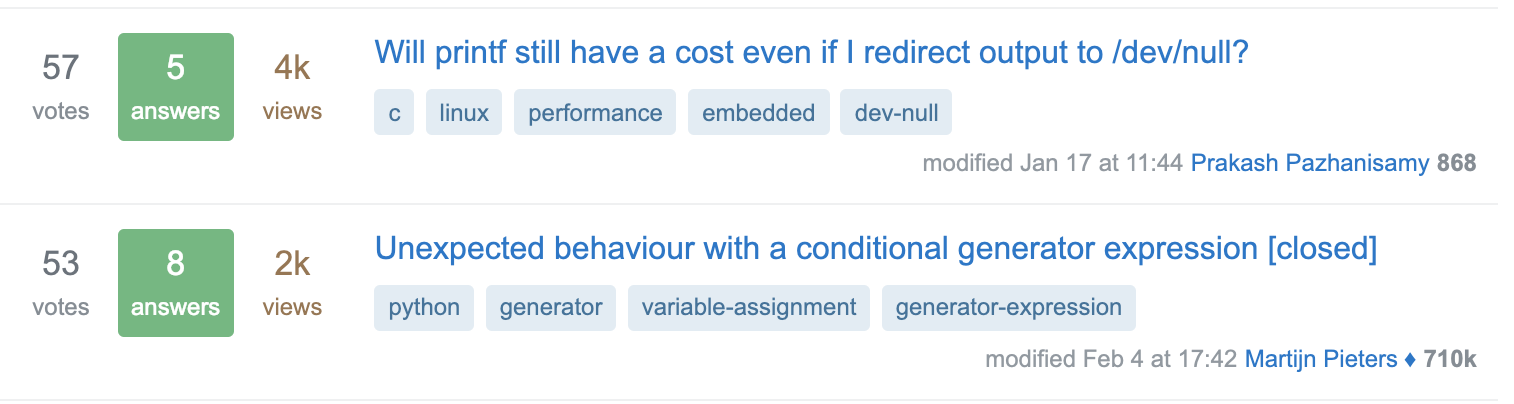
这样看似乎我们应该使用点赞(投票)率而非简单的点赞量来对文章进行打分,但是点赞率真的永远可信么? 我们再看一个例子


单从投票率来看,第一个问题投票率高达50%但是浏览量只有2 ,而第二个问题投票率较低但是浏览量很高。如果但从投票率来看,似乎第一个问题排名更高,但是直觉告诉我们第二个问题应该排名更靠前。这就涉及统计学中点估计的置信度问题。
让我们来把用户点赞这个行为抽象一下,我们假设每一个用户要么点赞要么拍砖,每一个用户之间的行为之间独立,所以每个用户\(\sim Bernoulli(p)\), 其中p是点赞的概率。当样本量足够大的时候,根据大数定律用户点赞的频率会趋于点赞率$\lim\limits_{x \to \infty} P(|\frac{n_x}{n} - p| < \epsilon)=1 $
但是当用户量不够,样本比较小的时候,计算的点赞率会和总体概率会存在较大的偏差。一种解决方法就是使用区间估计而非点估计,我们给出点赞率估计的下边界而非点赞率的估计值。
最常用的二项分布的区间估计由近似正态分布给出。根据大数定律,参数为n,p的二项分布在\(n \to \infty\)的时候 \(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}} \sim N(0,1)\)。根据正态分布的置信区间我们会得到二项分布的近似区间估计如下
\[
\begin{align}
& p( | \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} | < z_{\alpha/2}) = 1- \alpha \\
& where \, 置信度是0.95,\alpha = 0.05 \&\hat{p}是根据每个用户点赞行为给出的点赞率的估计\&n是样本量,可以是用户点赞+拍砖的总和,或者是用户浏览量\&p是总体的点赞率是我们希望得到的估计\\end{align}
\]
Wald Interval 对上述近似区间用样本估计\(\hat{p}\)替代总体p,给出了最常用的二项分布置信区间:
\[
\begin{align}
p_-,p_+ = \hat{p} \pm z_{\alpha/2}\sqrt{\hat{p}(1-\hat{p})/n}
\end{align}
\]
wald置信区间适用大多数情况,但是在下面三个情况下会存在问题:
而在估计文章点赞率这个场景下我们不可避免的会碰到上述3个情况,在这种情况我们往往会使用更加复杂的置信区间算法。来来来下面让我们说说其中一种高配版的置信区间- Wilson Interval
Wilson对Walt置信区间做了修正, Wilson置信区间的上下界如下:
\[
\begin{align}
p_-,p_+ = \frac{\hat{p} + \frac{z^2_{\alpha/2}}{2n}} {1 +\frac{z^2_{\alpha/2}}{n}} \pm z_{\alpha/2}\frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z^2_{\alpha/2}}{4n^2} }}{1 +\frac{z^2_{\alpha/2}}{n}}
\end{align}
\]
看着老复杂了,让我们来拆解一下你就会发现原理蛮好理解的。先说说对总体均值的估计,wilson对\(\hat{p}\)进行了如下调整:
\[
\begin{align}
\hat{p} \to \tilde{p} = \frac{\hat{p} + \frac{z^2_{\alpha/2}}{2n}} {1 +\frac{z^2_{\alpha/2}}{n}}
\begin{align}
\]
当样本量足够大Wilson和Walt对总体均值的估计会趋于一致。当样本量很小的时候, 不同于walt,wilson给样本估计加了一个\(\frac{1}{2}\)的贝叶斯前置概率(点赞和拍砖的概率各是50%),然后不断用新增样本来对这个前置概率进行调整。从而避免样本较小的时候样本估计过度偏离总体的问题。
\[
\begin{align}
when \lim\limits_{n \to \infty} \tilde{p} \to \hat{p} \when \lim\limits_{n \to 0} \tilde{p} \to \frac{1}{2} \\end{align}
\]
方差部分也做了相同的处理, 当样本足够大的时候wilson和walt对总体方差的估计会趋于一致,但是当样本小的时候和上述样本均值的处理方法一样,会趋于贝叶斯前置概率对应的方差\(\hat{p} \to \frac{1}{2} \Rightarrow \hat{p}(1-\hat{p}) \to \frac{1}{4}\)
\[
\begin{align}
\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \to \frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z^2_{\alpha/2}}{4n^2} }}{1 +\frac{z^2_{\alpha/2}}{n}}
\end{align}
\]
下面两张图片很直观的给出了不同样本数量(n=10 vs.100)下,样本均值的估计所对应的置信区间的长度(方差估计)。当样本大的时候Wilson和Wald几乎一样,当样本小的时候,随着p趋于0 or 1,Wilson置信区间会显著宽于Walt区间。

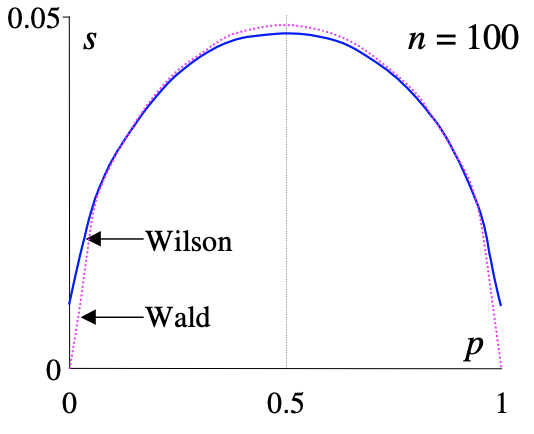
而Wilson打分就是取Wilson置信区间的下界:
\[
\begin{align}
score= \frac{\hat{p} + \frac{z^2_{\alpha/2}}{2n}} {1 +\frac{z^2_{\alpha/2}}{n}} - z_{\alpha/2} \frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z^2_{\alpha/2}}{4n^2} }}{1 +\frac{z^2_{\alpha/2}}{n}}
\end{align}
\]
Wilson打分方式有几个很好的特性:
Reference
标签:logs hat 第一个 计算 sandy tac 时间 方式 end
原文地址:https://www.cnblogs.com/gogoSandy/p/10358961.html