标签:转化 开始 prim 一起 结束 fine com 信息 std
接昨天,在这里给出图的其中一种应用:最小生成树算法(Prime算法和Kruskal算法)。两种算法的区别就是:Prime算法以顶点为主线,适合用于顶点少,边密集的图结构;Kruskal算法以边为主线,适合于顶点比较多,但是边比较稀疏的图结构。代码如下,亲测,可执行,在最后也给出输入数据的形式。
1 /*
2 图结构的最小生成树算法:
3 1.prime算法:按顶点查找,遍历当前顶点所有邻接边,选择权值最小值,
4 记录这两个顶点,直到所有的顶点都已处理
5
6 2.Kruskal算法:按边查找,将所有边的权值排序,以此选择权值最小的边,
7 检查该边连接的两个顶点是否状态一致(都已处理,或都未处理),
8 直到所有顶点都标记为处理过
9 */
10
11
12 #include<stdio.h>
13 #define INFINITY 65535
14 #define MAXVEX 100
15
16 //边集数组图结构
17 typedef struct //边结构体
18 {
19 int start;
20 int end;
21 int weight;
22 }Edges;
23
24 typedef struct //图结构
25 {
26 char Vex[MAXVEX]; //顶点数组
27 Edges edge[MAXVEX]; //边数组
28 int numVexes; //顶点数量
29 int numEdges; //边数量
30 }E_VGraph;
31
32 //邻接矩阵图结构
33 typedef struct
34 {
35 char Vex[MAXVEX]; //顶点数组
36 int arc[MAXVEX][MAXVEX]; //边数组
37 int numVexes; //顶点数量
38 int numEdges; //边数量
39 }Graph;
40
41 //邻接矩阵图结构转化为边集数组图结构,并将权值升序排序
42 void G_EVConversion(Graph G, E_VGraph *G1)
43 {
44 int i,j,k,lowest;
45 Edges edges[MAXVEX];
46 G1->numVexes = G.numVexes; //将邻接矩阵顶点数赋值于边集数组
47 G1->numEdges = G.numEdges; //将邻接矩阵边数赋值于边集数组
48 for(i = 0; i < G.numVexes; i++) //遍历邻接矩阵中的每个顶点
49 {
50 for(j = i+1; j < G.numVexes; j++) //遍历除当前结点之后的结点
51 {
52 if(G.arc[i][j] != INFINITY) //判断两顶点之间是否有边
53 {
54 edges[i].start = i; //记录当前边的起点
55 edges[i].end = j; //记录当前边的终点
56 edges[i].weight = G.arc[i][j]; //记录当前边的权重
57 printf("%d %d\n",G.arc[i][j],edges[i].weight);
58 }
59 }
60 }
61 printf("\n\n");
62 for(i = 0; i < G.numEdges; i++) //选择排序edges数组
63 {
64 lowest = INFINITY;
65 for(j = 0; j < G.numEdges; j++)
66 {
67 printf("%d %d %d\n",j,edges[j].weight,lowest);
68 if(edges[j].weight <= lowest)
69 {
70 lowest = edges[j].weight;
71 k = j;
72 printf("\n%d\n",k);
73 }
74 }
75 G1->edge[i].start = edges[k].start; //将每轮找出的最小权值的边的信息
76 G1->edge[i].end = edges[k].end; //写入边集数组中
77 G1->edge[i].weight = edges[k].weight;
78 edges[k].weight = INFINITY; //赋值完毕,将此最小权值设为最大值
79 printf("\n");
80 printf("%d\n",G1->edge[i].weight);
81 }
82 }
83
84 //确认函数
85 int Find(int *parent, int f)
86 {
87 if(parent[f] > 0) //检查此顶点是否处理过,若大于0,则处理过
88 f = parent[f]; //将parent[f]的值赋值给f
89 return f; //返回f
90 }
91
92 //克鲁斯卡尔算法构造最小生成树
93 void minTreeKruskal(E_VGraph G1)
94 {
95 int i,j,k,w,n,m;
96 int parent[MAXVEX]; //记录结点状态
97 int lowest = 0; //最小权值
98 for(i = 0; i < G1.numVexes; i++) //初始化记录数组,所有顶点记为未被处理
99 parent[i] = 0;
100 for(i = 0; i < G1.numEdges; i++) //遍历边集数组
101 {
102 n = Find(parent, G1.edge[i].start); //得到当前边的开始顶点的状态
103 m = Find(parent, G1.edge[i].end); //得到当前边的结束顶点的状态
104 if(n != m) //若状态不同(即,起点与终点一个处理过,一个未处理)
105 {
106 lowest += G1.edge[i].weight; //将此边的权值加入最小生成树权值
107 parent[G1.edge[i].start] = 1; //将起点记为处理过
108 parent[G1.edge[i].end] = 1; //将终点记为处理过
109 }
110 }
111 printf("克鲁斯卡尔算法构建最小生成树的权值为:%d\n", lowest);
112 }
113
114
115
116 void CreatGraph(Graph *G) //创建图结构
117 {
118 int i,j,k,w,a[100];
119 printf("请输入顶点与边的数量:");
120 scanf("%d,%d",&G->numVexes,&G->numEdges); //写入顶点数量与边的数量
121 for(i = 0; i < G->numVexes; i++) //初始化顶点数组
122 {
123 printf("请输入第%d个顶点:", i);
124 scanf("%c",&G->Vex[i]);
125 getchar();
126 }
127 for(i = 0; i < G->numVexes; i++) //初始化边数组
128 for(j = 0; j < G->numVexes; j++)
129 G->arc[i][j] = INFINITY;
130
131 for(k = 0; k < G->numEdges; k++) //构造边的数组
132 {
133 printf("请输入边的起点与终点的下标及其权重:");
134 scanf("%d,%d,%d",&i,&j,&w);
135 G->arc[i][j] = G->arc[j][i] = w; //无向图的对称性
136 }
137 printf("创建成功\n");
138 }
139
140 //Prim算法构造最小生成树
141 void minTreePrim(Graph G,int i)
142 {
143 int j,k,l,w,count,zongWeight;
144 int visited[MAXVEX]; //记录访问过的顶点
145 int lowest[MAXVEX]; //记录最小权值
146 for(j = 0; j < G.numVexes; j++) //初始化访问数组,将所有顶点记为未访问过
147 visited[j] = 0;
148 visited[i] = 1; //将传入顶点记为访问过
149 lowest[i] = 0; //将此顶点的权值记为0
150 zongWeight = 0; //总权重为0
151 count = 1; //访问过的顶点数量为1
152 int wei = INFINITY; //权重变量记为最大值
153 while(count < G.numVexes) //只要访问过的顶点数目小于图中顶点数目,继续循环
154 {
155 for(k = 0; k < G.numVexes; k++) //遍历访问过的顶点数组
156 {
157 if(visited[k] == 1) //如果当前顶点访问了,寻找它的邻接边
158 {
159 for(l = 0; l < G.numVexes; l++) //遍历图中所有顶点
160 {
161 if(visited[l] == 0 && G.arc[k][l] < wei) //如果未被访问,且权值小于权值变量
162 {
163 wei = G.arc[k][l]; //更新权值变量
164 w = l; //更新最小顶点
165 }
166 }
167 }
168 }
169 visited[w] = 1; //将最小权值顶点记为访问过
170 lowest[l] = wei; //记录他的权值
171 zongWeight += wei; //加入总权重
172 count++; //访问过的顶点数量+1
173 wei = INFINITY;
174
175 }
176 printf("最小生成树的权值为:%d\n",zongWeight);
177 }
178
179 void main()
180 {
181 Graph G;
182 E_VGraph G1;
183
184 printf("请构造图结构:\n");
185 CreatGraph(&G);
186
187 printf("\n\n");
188 printf("普利姆算法构建最小生成树\n");
189 minTreePrim(G,0);
190
191 printf("\n\n");
192 printf("克鲁斯卡尔算法构建最小生成树\n");
193 G_EVConversion(G, &G1);
194 minTreeKruskal(G1);
195 }
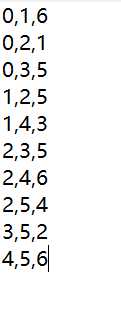
本来今天应该将最小生成树与最短路径的算法一起上传,但是我写的最短路径算法还有一些bug没调好,所以要延迟一天,勿怪。
标签:转化 开始 prim 一起 结束 fine com 信息 std
原文地址:https://www.cnblogs.com/yurui/p/10366617.html